CGAL的3D Alpha Wrapping

1、介绍

        几何建模和处理中的各种任务都需要将三维对象表示为有效的曲面网格，其中“有效”指的是不透水、无交叉、可定向和2流形的网格。这样的表示提供了内部/外部和测地线邻域的定义良好的概念。

        3D数据通常是通过测量和重建获得的，由人类设计，或通过不完美的自动化过程生成。因此，它们可以表现出各种各样的缺陷，包括间隙、数据丢失、自相交、退化（如零体积结构）和非流形特征。

        考虑到大量可能的缺陷，已经提出了许多方法和数据结构来修复特定的缺陷，通常目的是保证修复的3D模型中的特定特性。可靠地修复所有类型的缺陷是出了名的困难，并且通常是一个不适定问题，因为对于具有缺陷的给定3D模型存在许多有效的解决方案。此外，输入模型可能过于复杂，具有不必要的几何细节、虚假的拓扑结构、不必要的内部组件或过于精细的离散化。对于避免碰撞、路径规划或模拟等应用程序，获得输入的近似值可能比修复输入更重要。这里的近似值是指能够过滤掉内部结构、精细细节和空洞，并将输入包裹在用户定义的偏移范围内的方法。

        给定输入的三维几何，我们解决了计算保守近似的问题，其中保守意味着保证输出严格包围输入。我们寻求无条件的鲁棒性，因为输出网格应该是有效的（定向的，2-流形，并且没有自交叉），即使对于具有许多缺陷和退化的原始输入也是如此。默认输入是三维三角形的汤，但通用界面为其他类型的有限三维基本体（如三角形汤和点集）敞开了大门。

        收缩包装从三角形汤输出，有许多交叉点和间隙。从左到右依次为输入模型、输出环绕和叠加。 

        处理非流形特征和退化。从左到右，一个非流形顶点、自相交面和两个相邻的三角形表示零体积结构。该算法通过包装输入的偏移量来处理这些情况。

2、方法

        已经设计了许多方法来将3D模型封装在体积内，其特征在于近似的运行时间和质量（即紧密性）之间的不同平衡。在最简单的情况下，轴对齐或定向的边界框清楚地满足一些所需的特性；然而，近似误差是不可控的，并且往往非常大。计算输入的凸包也匹配了一些所需的属性，并提高了结果的质量，尽管代价是增加了运行时间。然而，近似值仍然很粗略，尤其是在有几个组成部分的情况下。

        事实上，凸包是阿尔法形状的一个特例。从数学上讲，阿尔法形状是Delaunay三角剖分的一个子复合体，简化是复合体的一部分，这取决于其最小（空）Delaunay球的大小。直观地说，构建3D阿尔法形状可以被认为是用用户定义的半径为阿尔法的空球雕刻3D空间。阿尔法形状产生了形状的可证明的、良好的分段线性近似，但是在点集上定义的，而我们希望处理更通用的输入数据，如三角形汤。即使在对三角形汤进行采样后，阿尔法形状也不能保证对任何阿尔法都是保守的。最后，内部结构也被雕刻在卷内，而不是被过滤掉。

        受阿尔法形状的启发，我们用收缩包装取代了上述雕刻的概念：我们从包围输入的简单三维Delaunay三角剖分开始，迭代构建三维Delaunay三角剖分的子复合体，然后迭代移除位于复合体边界上的合格四面体。此外，随着收缩的进行，基本的三角剖分以及由此产生的复杂情况也被细化了。因此，我们不是像阿尔法形状那样从输入数据的凸包中雕刻，而是通过类似Delaunay精化的算法构建一个全新的网格。细化算法在偏移体积的边界上插入Steiner点，偏移体积定义为到输入的无符号距离字段的水平集。

        该过程既防止在输出中创建内部结构，又避免了多余的计算。此外，将我们的网格结构与输入的几何结构和离散化分离有几个优点：（1）底层数据不限于特定格式（三角形汤、多边形汤、点云等），因为所需的只是回答三个基本的几何查询：（a）点和输入之间的距离，（b）查询点在输入上的投影，（c）四面体和输入之间的交叉测试，以及（2）用户有更多的自由度来交换对输入的紧密性以获得最终的网格复杂性，因为在输入的大偏移上构建保守近似需要更少的网格元素。

 2.1、算法

        初始化。该算法通过将一个松散边界框的八个角顶点插入到3D Delaunay三角剖分中来初始化。在CGAL的3D Delaunay三角剖分中，所有三角形面都与两个四面体单元相邻。与三角剖分顶点凸包的一个面重合的Delaunay三角剖分边界的每个面都与所谓的无限四面体单元相邻，这是一个与所谓的无限顶点相连的抽象单元，以确保上述双面邻接。最初，所有无限单元都被标记为外部，所有有限四面体单元都被标记为内部。

        收缩包装。收缩包装算法从外到内遍历Delaunay三角剖分的单元，从一个单元到其相邻单元进行洪水填充，并尽可能将相邻单元标记为外部（术语“可能”稍后指定）。洪水填充是通过一个表示面两个相邻单元之间从外到内遍历的Delaunay三角剖分面的优先级队列实现的。这些三角面在下文中称为门。

        给定一个外部单元及其相邻的内部单元，如果其外接圆半径大于用户定义的参数α，则共同面（即门）被称为α可遍历，其中外接圆半径是指相关三角形的Delaunay球的半径。直观地说，小于α的腔是不可访问的，因为它们的门不是α可遍历的。

        通过凸包上的α遍历门初始化，优先队列仅包含α遍历门，并按门的外接圆半径降序排列。遍历可以看作是一个连续的过程，沿着门的对偶沃罗诺伊边前进，用一束空球环绕门。

        （左）二维Delaunay三角剖分（黑色）中Delaunay边（绿色）外接的空心圆（蓝色）的铅笔。从顶部三角形圆心c1到底部三角形圆心c2，由e（点红）表示的对偶Voronoi边是没有Delaunay顶点的最大圆的中心的轨迹。（右）对应于左示例的图形。x轴对应于位于Voronoi边e上的空圆心的位置，从c1到c2。y轴是相应空圆的半径值。在这种情况下，空圆的铅笔的最小半径位于绿色Delaunay边的中点。在我们的算法中，当空圆的铅笔的最小半径小于阿尔法时，门（绿色Delaunay边）被认为是不可阿尔法遍历的。

        当通过α可遍历面f从外部单元co遍历到内部单元ci时，会测试两个标准以防止包裹过程与输入碰撞：

        (1) 我们检查 f 的对偶沃罗诺伊边（即两个入射单元的圆心之间的线段）与偏移曲面之间的交点，偏移曲面定义为输入的无符号等值面的水平集。如果存在一个或多个交点，则沿从外到内的对偶沃罗诺伊边将第一个交点作为斯坦纳点插入三角剖分中。

        (2) 如果双沃罗诺伊边不与偏移曲面相交，但相邻单元 ci 与输入相交，则计算 ci 的圆心在偏移曲面上的投影，并将其作为斯坦纳点插入三角剖分中（这会破坏 ci）。

        在上述每个斯坦纳点插入之后，所有新的事件单元都被标记为内部，并且新近的阿尔法可穿越门被推入优先级队列。

        如果上述两个条件都不满足，则遍历邻近单元 ci 并标记为外部。将 ci 的阿尔法可遍历面作为新门推入优先级队列，这些面将内部单元与外部单元分开。

        一旦队列清空（由于插入新的斯坦纳点，面（及其外接圆）变小），构建阶段即告结束。输出三角形曲面网格从Delaunay三角剖分中提取出来，作为将内部单元与外部单元分隔开的面集。

        下图描述了2D中算法的步骤。

        二维收缩包装算法的步骤。通过将输入（红色）的松散边界框的角插入Delaunay三角测量中来初始化该算法，并且所有有限三角形都在内部标记（灰色）。从队列中弹出的当前门（绿色边缘）是可遍历的。当大门附近的三角形与输入不相交时，它会被标记在外面，并且新的阿尔法可遍历大门会被推到队列中。当相邻三角形与输入相交时，计算一个新的Steiner点（大的绿色圆盘）并将其插入三角测量中，所有相邻三角形都在内部标记，新的alpha可遍历门被推到队列中，然后恢复遍历。灰色边缘描绘了Delaunay三角测量。蓝色边表示Voronoi图。粉红色的圆圈表示半径为alpha的空圆圈。输出边（深蓝色）将内部三角形与外部三角形分开。 

2.2、保证

        该算法被证明是终止的，并产生了一个严格包围输入数据的2-流形三角网格。证明的关键要素是我们从外到内进行包裹，并且永远不允许与输入相交的单元被标记为内部。此外，导致三角化细化的两个标准都插入了斯坦纳点，这些斯坦纳点可以保证打破需要细化的单元，并减小相邻面的圆周半径。

        由于主要的细化标准是在对偶沃罗诺伊边缘和输入偏移之间插入交点，或将沃罗诺伊顶点投影到输入偏移上，该算法与基于德劳内滤波和细化的流行网格算法有相似之处。

3、接口

        我们的算法以一组 3D 三角形作为输入，这些三角形可以作为三角形汤或三角形表面网格提供，以及两个用户定义的标量参数：alpha 和偏移值。它从输入的宽松边界框开始，通过收缩包裹和细化 3D Delaunay 三角剖分。参数 alpha 指的是包裹过程中无法遍历的腔或孔的大小，因此也指最终的细节级别，因为 alpha 就像普通 Delaunay 细化算法中的尺寸字段。参数偏移是指细化三角剖分和输入的顶点之间的距离，因此大的偏移转化为对输入的宽松包围。第二个参数提供了一种控制紧密度和复杂度之间权衡的方法。

        该组件的主要入口点是生成alpha包裹的全局函数CGAL::alpha_wrap_3()；该函数以多边形汤或多边形网格为输入。输入连接没有先决条件，因此它可以接受任意三角形汤，包括岛、自交点或重叠，以及组合或几何退化。

        底层特征类必须是内核概念的模型。它应该使用浮点数类型，因为算法固有的不精确性，因为偏移表面上没有新顶点的闭合形式描述。

        输出是一个三角形表面网格，其类型由用户选择，前提是它必须是 MutableFaceGraph 概念的模型。

4、参数选择

        算法的两个参数影响输出网格的细节级别和复杂性。

4.1、Alpha

        主要参数alpha控制着在收缩包裹过程中德劳内面是否可遍历。alpha的主要目的是控制包裹过程中使用的空球的大小，从而确定哪些特征将出现在输出中：事实上，如果面的外接圆半径大于alpha，则该面是alpha可遍历的；因此，该算法只能收缩包裹直径大于alpha的狭长地带或孔洞。第二个不那么直接的结果是，只要面的外接圆半径大于alpha，则单元内的入射点将被访问并可能被细化。因此，当算法终止时，所有面的外接圆半径都小于alpha。因此，该参数也表现为输出三角形面的尺寸标准。

        alpha参数对输出的影响。（左）由原始点云曲面重建生成的输入三角形网格具有许多非流形边和顶点、多余的几何细节和虚假的拓扑结构。（右）此组件保守地近似输入，并根据alpha参数生成对输入具有不同复杂度和保真度的有效网格。α越小，收缩包装过程进入空腔的深度就越深。alpha参数从左到右分别减小到输入边界框最长对角线的1/50、1/100和1/300。一个大的alpha将产生一个不那么复杂但不那么忠实于输入的输出。 

4.2、偏移

        第二个参数是偏移距离，它控制着与的距离，从而控制着输出网格顶点所在的偏移等值面的定义。这个参数控制着结果的紧密度，这输入反过来又会产生一些后果。首先，将顶点定位在远离输入的位置，使算法能够生成一个不太复杂的网格，特别是在凸区域。这种行为的简单例子是一个非常密集的球体网格，对于这个网格，尽可能紧密的包络也会非常密集。其次，等值面离输入越远，通过第一个标准插入的新点就越多（即通过与对偶沃罗诺伊边的交集，见算法部分）；因此，输出质量在三角形元素的角度方面得到了提高。最后，根据alpha参数的值，大的偏移也可以提供故障检测能力。然而，使用小的偏移参数往往会更好地保持锐利特征，因为投影斯坦纳点往往会投影到凸锐利特征上。

         偏移参数对输出的影响。（左）通过在参数空间中对NURBS CAD模型进行网格划分生成的输入网格。（右）偏移越小，采样点离输入越近。偏移参数从左到右分别减小到输入边界框最长对角线的1/50、1/200和1/1000。对于所有级别的细节，alpha参数等于输入边界框最长对角线的1/50。偏移量越大，输出越不复杂，三角形质量越好。但是，当偏移参数较小时，尖锐特征（红色边）会得到很好的保留。

        斯坦纳指出。投影Steiner点（绿色）是通过将三角形的圆心投影到偏移量上来计算的。交点Steiner点（蓝色）被计算为Voronoi边和偏移之间的第一个交点。（左）当偏移参数较小时，该算法产生更多的投影Steiner点，这有助于提高凸尖特征的保留率。（右）当偏移参数较大时，该算法会生成更多的相交Steiner点，这往往会在3D中生成角度质量更好的三角形。 

        默认情况下，我们建议将偏移参数设置为alpha的一小部分，以便alpha成为控制最终细节级别的主要参数。下图说明了这两个参数的影响。 

         自行车模型上的不同alpha和偏移值（533000个三角形）。x轴表示从左到右等于输入边界框最长对角线的1/5000、1/2000、1/500、1/200、1/5的偏移值。y轴表示从下到上等于输入边界框最长对角线的1/300、1/100、1/50、1/20和1/5的alpha值。每个细节级别下面的数字表示三角形的数量。根据alpha值的不同，偏移过小或过大将产生具有更高复杂性的输出网格。对于每个阿尔法，具有较低复杂度的模型可以用作从近距离到远距离的碰撞检测的比例空间表示。 

4.3、关于“双面”包装的一点注记

        偏移参数对我们的方法至关重要，因为它保证了输出是一个封闭的2-流形曲面网格。事实上，即使输入是一个零体积的结构，如单个3D三角形，输出包络也是一个包围所述三角形的薄体积。

        用户应该记住，包裹算法无法确定它是作用于无符号距离场的内部还是外部，因此在输入中有孔并且alpha值小于孔尺寸的情况下，会产生双侧包裹。

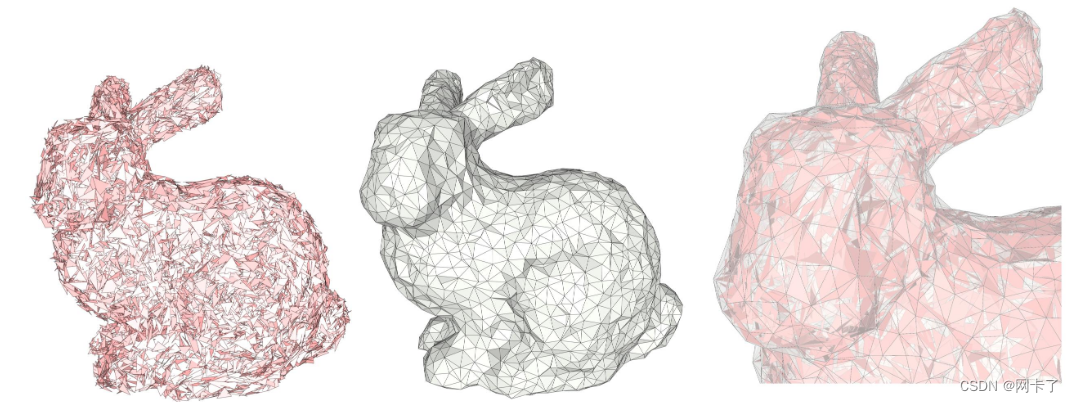
        双面包裹。（左）在2D中包裹兔子，alpha的值递减。（右）在3D中包裹一只充满缺陷的兔子。最右边的一列描绘了内部的剪辑可视化。当alpha相对于孔的直径足够小时，该算法会生成双面包裹。 

5、性能

        下表绘制了Thingi10k数据集上包装算法的计算时间，以及输出三角形网格的复杂性。

        Thingi10k数据集上不同alpha值的执行时间和输出复杂性。Alpha从边界框对角线长度的1/20增加到1/200。x轴表示输出包裹网格的复杂度（以三角形小平面的数量表示）。y轴表示总计算时间，单位为秒。点的颜色和直径表示输入三角形汤中的面数，范围从10（绿色）到3154000（蓝色）。

6、其他

        Triangle Soup的使用可以包括以下几个方面：三角剖分：给定一组顶点，Triangle Soup可以使用三角剖分算法将这些顶点连接成一系列三角形，从而创建一个三角网格。这种剖分方法可以根据不同的算法和参数设置进行优化，以满足特定的需求。网格处理：一旦创建了三角网格，Triangle Soup可以提供各种工具和功能来处理这些网格。例如，可以对网格进行平滑处理、去除噪声、修复错误等操作，以改善网格的质量和准确性。纹理映射：Triangle Soup支持将纹理映射到三角网格上。这可以通过将纹理图像与网格的顶点坐标进行关联来实现，从而在渲染过程中为三角网格添加细节和外观。渲染和可视化：使用Triangle Soup创建和处理的三角网格可以用于渲染和可视化目的。可以将三角网格导入到图形渲染引擎或软件中，并使用适当的材质和光照设置进行渲染，生成具有真实感的图像或动画。

        阿尔法形状（Alpha Shape）是一种在计算机图形学和计算机辅助设计中常用的形状描述方法。它通过将一个物体或图形分解为一系列的三角形面片来表示，从而实现对物体的几何形状和表面属性的描述和渲染。阿尔法形状被广泛应用于三维建模和渲染领域，它可以描述物体的几何形状、表面纹理、透明度和光照效果等属性。