下列图片来自李宏毅老师的transformer课程ppt
课程地址:强烈推荐!台大李宏毅自注意力机制和Transformer详解!_哔哩哔哩_bilibili
引入:我们想要计算出一个序列中a1和a2、a3、a4的相关性,得到一个向量b1

下述讨论的注意力机制是Scaled Dot-Product Attention(缩放点积注意力),也是Attention Is All
You Need论文中介绍的注意力机制。

1、数学表示
自注意力机制的数学表示如下:

注释:
1、Query、Key和Value矩阵
- Query矩阵(Q):表示当前的关注点或信息需求,用于与Key矩阵进行匹配。
- Key矩阵(K):包含输入序列中各个位置的标识信息,用于被Query矩阵查询匹配。
- Value矩阵(V):存储了与Key矩阵相对应的实际值或信息内容,当Query与某个Key匹配时,相应的Value将被用来计算输出。
2、点积计算
通过计算Query矩阵和Key矩阵之间的点积(即对应元素相乘后求和),来衡量Query与每个Key之间的相似度或匹配程度。
3、缩放因子
由于点积操作的结果可能非常大,尤其是在输入维度较高的情况下,这可能导致softmax函数在计算注意力权重时进入饱和区。为了避免这个问题,缩放点积注意力引入了一个缩放因子,通常是输入维度的平方根。点积结果除以这个缩放因子,可以使得softmax函数的输入保持在一个合理的范围内。
4、Softmax函数
将缩放后的点积结果输入到softmax函数中,计算每个Key相对于Query的注意力权重。Softmax函数将原始得分转换为概率分布,使得所有Key的注意力权重之和为1。
5、加权求和
使用计算出的注意力权重对Value矩阵进行加权求和,得到最终的输出。这个过程根据注意力权重的大小,将更多的关注放在与Query更匹配的Value上。
其中的Q,K,V矩阵由n个q,k,v向量组成,n为输入序列向量的个数。
q向量 = a向量*矩阵wq
k向量 = a向量*矩阵wk
v向量 = a向量*矩阵wv
1.1、理解q,k,v
注意力机制中有两个输入:
查询序列q:正在处理的序列
上下文序列k,v:被关注的序列
1、通过q向量和k向量的点积可以得到注意力分数
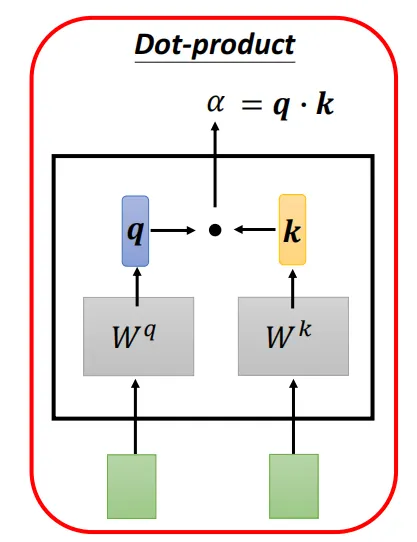

2、再经过一些处理和softmax把注意力分数转化成注意力权重

3、最后注意力权重和v向量相乘=注意力向量

这个操作常常被比作字典查找,但是,是一个模糊的,可微分的,向量化的字典查找。
举个例子,假设有一个普通的Python字典,有3个键和3个值,被传递了一个单独的查询:
d = {'color': 'blue', 'age': 22, 'type': 'pickup'}
result = d['color']查询(q)是你要匹配的内容,键(k)表示键,而值(v)则是键对应的信息;在普通的字典查找中,字典会找到匹配的键,并返回其对应的值;如果查询找不到完全匹配的键,也许你会期望返回最接近的值,比如在上面的例子中,如果你查找“d["species"]”,你可能会期望返回“pickup”,因为它是最接近查询的匹配。
一个注意力层就像是这样的一个模糊查找,但它不仅仅是寻找最佳键;它结合了查询(q)和键(k)向量,来确定它们匹配的程度,也就是“注意力分数”。然后,根据“注意力分数”对所有值进行加权平均;在注意力层中,每个位置的查询(q)序列都提供一个查询向量,而上下文序列则充当了一个字典,每个位置提供一个键和值向量。
补充知识:softmax层
Softmax函数是一种常用的激活函数,通常用于多分类任务的最后一层。它的作用是将一个实数向量转换成概率分布,所有输出的值介于 0 和 1 之间,并且所有输出值的总和为 1。
Softmax的公式如下:

解释:
- Softmax 对每个输入值 zi 计算一个指数值,这样可以确保所有输出值都为正数,并且它们对输入值的相对大小敏感。
- 然后,每个 zi被它对应的指数值除以所有输入值的指数和,这样所有的输出值就变成了概率,且概率和为 1。
举个例子:
假设我们有 一个包含 3 个元素的输入向量 z=[2.0,1.0,0.1]。
1、计算每个元素的指数:
e的2.0次方=7.389
e的1.0次方=2.718
e的0.1次方=1.105
2、计算所有指数的总和:
总和=7.389+2.718+1.105=11.212
3、计算softmax输出:
softmax(z1)=7.389/11.212=0.659
softmax(z2)=2.718/11.212=0.243
softmax(z3)=1.105/11.212=0.098
因此softmax输出为:
[0.659,0.243,0.098]
这个输出表示输入向量中的每个元素对应的类别概率,和为1
2、矩阵表示
在实际的计算中,为了方便并行计算注意力向量,向量运算会由矩阵运算完成
2.1、Q、K、V矩阵
q,k,v向量组成Q,K,V矩阵

2.2、注意力分数的计算

2.3、注意力向量的计算

3、训练参数
上面从数学和矩阵两个角度介绍了自注意力机制的原理,还有一个问题:作为一个神经网络结构,它在训练过程中学习的参数是什么呢?
就是我们提到过的三个线性变换矩阵,WQ、WK和WV

在Self-Attention机制中,WQ、WK和WV是三个关键的可学习参数矩阵,在模型初始化时随机生成,训练过程中通过梯度下降优化,以便生成合适的Q,K,V来进行注意力权重的计算。这样模型就能学习到如何有效地捕捉序列内部的依赖关系。
3.1、作用
- WQ(Query矩阵):将输入序列X映射到查询(Query)空间,用于计算注意力权重中每个位置对其他位置的“关注程度“。
- WK(Key矩阵):将输入序列X映射到键(Key)空间,与Query共同决定不同位置之间的相关性。
- WV(Value矩阵):将输入序列X映射到值(Value)空间,包含实际用于加权求和的信息,生成最终的注意力输出。
3.2、维度
- 输入矩阵X的维度为(n, d),其中n为序列长度,d为输入特征维度。
- WQ、WK、WV的维度通常为(d, dk),其中dk是投影后的维度(例如在Transformer中,dk = d / h,h为多头注意力的头数)。
- 投影后的Q、K、V维度为(n, dk),确保后续点积计算的兼容性。
3.3、获取方式
- 初始化:训练开始时,这些矩阵通过随机初始化(如Xavier或He初始化)生成。
- 学习过程:在模型训练过程中,通过反向传播和梯度下降算法优化这些矩阵的参数,使它们能够适应任务需求,有效捕捉输入序列的依赖关系。
3.4、示例
假设输入维度d=512,多头注意力头数h=8,则每个头的dk=64。此时:
- WQ、WK、WV的维度均为(512, 64)。
- 输入X经过映射后,Q、K、V的维度为(n, 64),每个头独立计算注意力,最终拼接结果。
4、多头自注意力机制
它允许模型同时关注来自不同位置的信息。通过线性变换分割Q,K,V矩阵到多个头(head),每个头都能独立地学习不同的注意力权重,从而增强模型对输入序列中不同部分的关注能力。
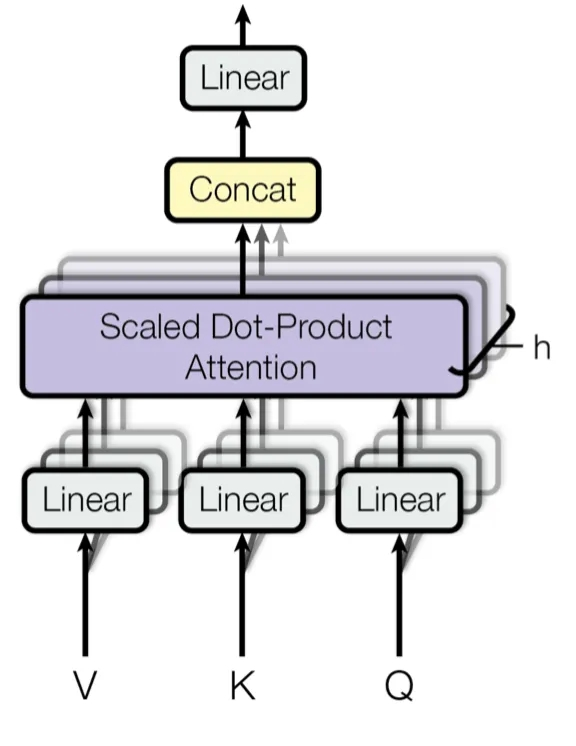
4.1、模型计算
相关性有很多种不同的形式,我们可以有多个q,k,v向量来计算不同形式的相关性。

接着,重复自注意力机制的计算,得到的每个注意力向量的维度为dk = d / h,h为多头注意力的头数)。将同一个位置的注意力向量拼接在一起再经过一些操作得到最终的注意力向量bi



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








