Permutations II

Questions:

思路:

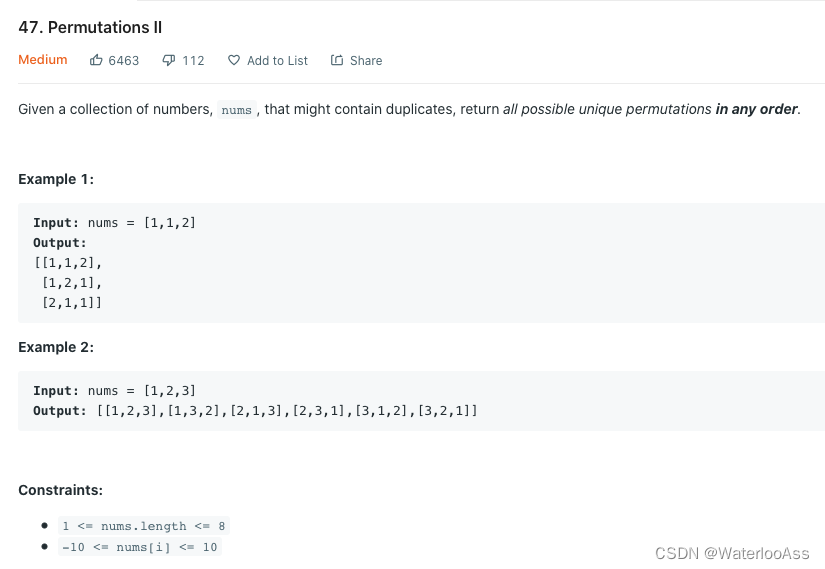
首先这一类题型呢, 找combinations, permutations, balabala 都可以用dfs (backtracking)来做, 不过针对每个提醒题型都会有一些方法使用上的区别.

针对这个permutation II呢,它和permutation那道题的区别就是这道题会存在duplicaets, 而我们的答案中不可以有duplicate,
就像普通permutation那道题, given nums[] = [1,1,2]
用permutation那道题的方法, 我们一开始就把List combs = nums. = [1,1,2]
然后在backtracking 中 我们swap每个element的位置, 从而达到取得permutation的目的, 但是按照老方法处理这道permutation II 是没法remove duplicates的,
所以我们要做一些改变, 我们对backtracking的改变也可以顺便应用在permutation那道题上，
就是我们这次变成,starting with a empty List, then add nums into it. and we record the visited numbers.
就是说, 我们这次的方法就是一个一个加element进list, 然后做backtrack, 当recursion 返回之后，再把前面加进list的element 删除, 这样来达成找到所有permutation的目的.
因为每一个number in numbers只能用一次, 所以我们要有一个visited[] 来记录当前combs里哪些element已经在了。

然后针对这个题, 怎么排出duplicate呢, 就是当我们backtrack的时候, 比如说[1,1,2]
当我们从第一个1开始找组合的时候, 第二个1还没用过, 也就是说这个时候我们是第一次创造,[1,1,x]的组合。所以此时OK，没问题。
但是当我们backtrack之后,我们第一个1开始找组合的loop结束， 要开始从第二个1开始找组合时, 我们就重复了。 因为1已经当过原先combs里的第一个element了. 此时我们只会又得到一个[1,1,x]的组合.
所以我们要avoid这种 duplication
所以呢, 当visited[i-1] == false && nums[i] == nums[I-1] 的时候, 就代表有duplicate 了.
为什么是visited[I-1] == false呢, 因为在我们backtracking中, 但凡visited[i-1] = false了, 就代表此时已经backtrack回来了. 就是所谓的第一个1开始找组合的loop已经结束了. 现在要开始从第二个1找组合了.
同时nums[I] == nums[i-1] 是duplicate的另一个条件

    public List<List<Integer>> permuteUnique(int[] nums) {
        List<List<Integer>> list = new ArrayList<>();
        Arrays.sort(nums);
        backtrack(list, new ArrayList<>(), nums, new boolean[nums.length]);
        return list;
    }

    private void backtrack(List<List<Integer>> list, List<Integer> tempList, int [] nums, boolean [] used){
        if(tempList.size() == nums.length){
            list.add(new ArrayList<>(tempList));
        } else{
            for(int i = 0; i < nums.length; i++){
                if(used[i] || i > 0 && nums[i] == nums[i-1] && !used[i - 1]) continue;
                used[i] = true; 
                tempList.add(nums[i]);
                backtrack(list, tempList, nums, used);
                used[i] = false; 
                tempList.remove(tempList.size() - 1);
            }
        }
    }