每日一题——Python实现PAT乙级1050 螺旋矩阵（举一反三+思想解读+逐步优化）6千字好文

本文链接：https://blog.csdn.net/weixin_44915521/article/details/140097807

一个认为一切根源都是“自己不够强”的INTJ

个人主页：用哲学编程-CSDN博客
专栏：每日一题——举一反三
 Python编程学习
 Python内置函数

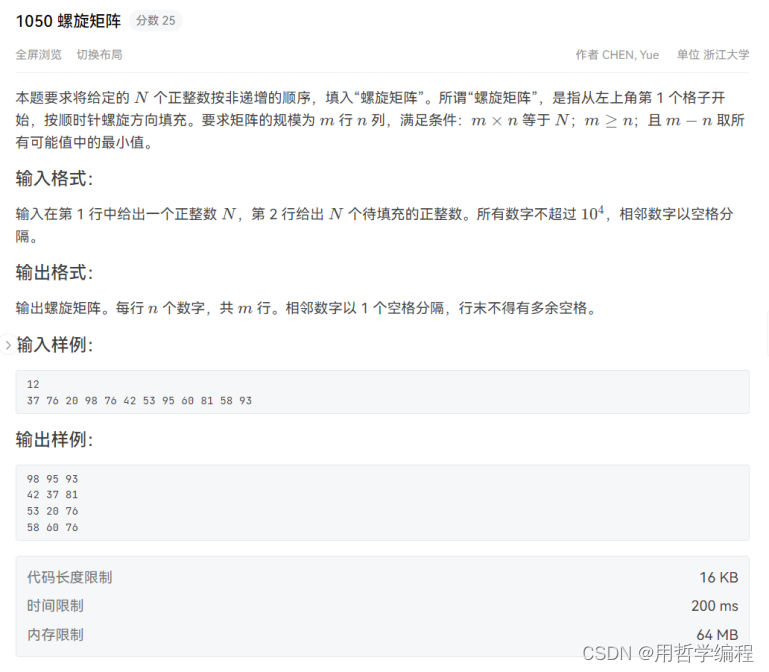
题目链接：https://pintia.cn/problem-sets/994805260223102976/exam/problems/type/7?problemSetProblemId=994805275146436608&page=0

我的写法

import math

# 读取矩阵元素的数量
N = int(input())
# 读取数字列表并按降序排序
nums = list(map(int, input().split()))
nums.sort(reverse=True)

def find_dimensions(N):
    # 找到最接近N的平方根的整数
    middle = math.isqrt(N)
    # 从middle开始向上找，直到找到两个数乘积为N
    for i in range(middle, N+1):
        for j in range(middle, 0, -1):
            if i * j == N:
                return i, j

def create_spiral_matrix(N, nums, m, n, seq_paces):
    # 初始化矩阵
    matrix = [[0 for i in range(n)] for j in range(m)]
    index_matrix = [0, -1]  # 矩阵索引初始位置
    index_nums = 0  # 数字列表索引
    for i in range(len(seq_paces)):
        if i % 4 == 0:  # 向右移动seq_paces[i]步
            index_matrix[1] += 1
            for j in range(seq_paces[i]):
                matrix[index_matrix[0]][index_matrix[1] + j] = nums[index_nums]
                if j == seq_paces[i] - 1:
                    index_matrix[1] = index_matrix[1] + j
                index_nums += 1
        elif i % 4 == 1:  # 向下移动seq_paces[i]步
            index_matrix[0] += 1
            for j in range(seq_paces[i]):
                matrix[index_matrix[0] + j][index_matrix[1]] = nums[index_nums]
                if j == seq_paces[i] - 1:
                    index_matrix[0] = index_matrix[0] + j
                index_nums += 1
        elif i % 4 == 2:  # 向左移动seq_paces[i]步
            index_matrix[1] -= 1
            for j in range(seq_paces[i]):
                matrix[index_matrix[0]][index_matrix[1] - j] = nums[index_nums]
                if j == seq_paces[i] - 1:
                    index_matrix[1] = index_matrix[1] - j
                index_nums += 1
        elif i % 4 == 3:  # 向上移动seq_paces[i]步
            index_matrix[0] -= 1
            for j in range(seq_paces[i]):
                matrix[index_matrix[0] - j][index_matrix[1]] = nums[index_nums]
                if j == seq_paces[i] - 1:
                    index_matrix[0] = index_matrix[0] - j
                index_nums += 1
    return matrix

def calculate_sequence_paces(N, m, n):
    # 计算螺旋填充的步数序列
    if m == 1:
        return [n]
    elif n == 1:
        return [1, m - 1]
    seq_paces = []
    dif = 0
    for i in range(N):
        if i == 0:
            seq_paces.append(n)
            dif += 1
            continue
        if i % 2 == 1:
            seq_paces.append(m - dif)
        elif i % 2 == 0:
            seq_paces.append(n - dif)
            dif += 1
        if seq_paces[-1] == 0:
            return seq_paces[:-1]
    return seq_paces

# 找到矩阵的维度
m, n = find_dimensions(N)
# 计算螺旋填充的步数序列
seq_paces = calculate_sequence_paces(N, m, n)
# 创建螺旋矩阵
matrix = create_spiral_matrix(N, nums, m, n, seq_paces)
# 输出矩阵
for row in matrix:
    print(*row)

时间复杂度分析

排序：对 N 个数字进行排序的时间复杂度是 O(N log N)。
find_dimensions：这个函数在最坏情况下需要检查大约 sqrt(N) 个可能的行和列组合，因此时间复杂度大约是 O(N)。
calculate_sequence_paces：这个函数在最坏情况下需要遍历 N 次，时间复杂度也是 O(N)。
create_spiral_matrix：这个函数需要遍历所有步数序列，步数序列的长度大约是 sqrt(N)，每次填充矩阵的时间复杂度是 O(N)，所以总时间复杂度也是 O(N)。

综合来看，主要的时间消耗来自于排序和矩阵填充，因此总时间复杂度是 O(N log N)。

空间复杂度分析

排序：排序需要的额外空间复杂度是 O(N)。
矩阵：矩阵的大小是 O(N)。
步数序列：步数序列的大小大约是 sqrt(N)。

综合来看，主要的空间消耗来自于矩阵和排序，因此总空间复杂度是 O(N)。

总结

这段代码在功能上实现了将一组数字按螺旋顺序填充到矩阵中，并且在时间和空间复杂度上都是高效的。代码结构清晰，函数职责明确，易于理解和维护。主要的时间消耗来自于排序和矩阵填充，而空间消耗主要由矩阵和排序决定。总体来说，这是一段设计良好且高效的代码。

我要更强

为了解决这个问题，我们需要完成以下步骤：

读取输入的数字数量 N 和数字列表。
对数字列表进行降序排序。
找到满足 m * n = N 且 m >= n 的矩阵维度 m 和 n，并且使得 m - n 最小。
创建一个空的螺旋矩阵，并按照顺时针方向填充数字。
输出填充好的螺旋矩阵。

以下是实现上述步骤的Python代码：

import math

# 读取输入
N = int(input())
nums = list(map(int, input().split()))

# 对数字列表进行降序排序
nums.sort(reverse=True)

# 找到合适的矩阵维度
def find_dimensions(N):
    min_diff = float('inf')
    m, n = 0, 0
    for i in range(1, int(math.sqrt(N)) + 1):
        if N % i == 0:
            j = N // i
            if j >= i and j - i < min_diff:
                min_diff = j - i
                m, n = j, i
    return m, n

m, n = find_dimensions(N)

# 创建并填充螺旋矩阵
matrix = [[0] * n for _ in range(m)]
top, bottom, left, right = 0, m - 1, 0, n - 1
index = 0

while top <= bottom and left <= right:
    # 向右填充
    for i in range(left, right + 1):
        matrix[top][i] = nums[index]
        index += 1
    top += 1

    # 向下填充
    for i in range(top, bottom + 1):
        matrix[i][right] = nums[index]
        index += 1
    right -= 1

    # 向左填充
    if top <= bottom:
        for i in range(right, left - 1, -1):
            matrix[bottom][i] = nums[index]
            index += 1
        bottom -= 1

    # 向上填充
    if left <= right:
        for i in range(bottom, top - 1, -1):
            matrix[i][left] = nums[index]
            index += 1
        left += 1

# 输出螺旋矩阵
for row in matrix:
    print(' '.join(map(str, row)))

代码解释

输入读取：首先读取输入的数字数量 N 和数字列表 nums。
排序：对数字列表 nums 进行降序排序。
找到矩阵维度：定义 find_dimensions 函数来找到合适的矩阵维度 m 和 n，使得 m * n = N 且 m >= n，并且 m - n 最小。
填充矩阵：创建一个空的矩阵 matrix，并使用边界指针（top, bottom, left, right）来控制填充方向，按照顺时针方向填充数字。
输出矩阵：最后，输出填充好的螺旋矩阵。

这个代码在时间和空间复杂度上都是高效的，并且能够正确地解决给定的问题。

代码结构和逻辑

输入处理：代码首先读取输入的数字数量 N 和数字列表 nums，这一部分的时间复杂度是 O(N)，因为需要读取和存储 N 个数字。
排序：对数字列表 nums 进行降序排序，使用的是 Python 内置的 sort 方法，其时间复杂度是 O(N log N)。
找到矩阵维度：定义 find_dimensions 函数来找到合适的矩阵维度 m 和 n。这个函数的时间复杂度是 O(sqrt(N))，因为它只需要遍历到 sqrt(N) 的整数。
填充矩阵：创建一个空的矩阵 matrix，并使用边界指针（top, bottom, left, right）来控制填充方向，按照顺时针方向填充数字。这一部分的时间复杂度是 O(N)，因为每个数字只被处理一次。
输出矩阵：最后，输出填充好的螺旋矩阵。这一部分的时间复杂度也是 O(N)，因为需要遍历并输出每个元素。

时间复杂度

综合以上分析，主要的时间消耗来自于排序和矩阵填充。因此，总的时间复杂度是 O(N log N)。

空间复杂度

输入存储：需要存储 N 个数字，空间复杂度是 O(N)。
排序：排序过程中需要额外的空间，但由于 Python 的 sort 方法是原地排序，所以这部分的空间复杂度可以忽略不计。
矩阵存储：需要存储一个 m * n 的矩阵，空间复杂度是 O(N)。

因此，总的空间复杂度是 O(N)。

总结

这段代码在功能上实现了将一组数字按螺旋顺序填充到矩阵中，并且在时间和空间复杂度上都是高效的。代码结构清晰，函数职责明确，易于理解和维护。主要的时间消耗来自于排序和矩阵填充，而空间消耗主要由矩阵和输入数据决定。总体来说，这是一段设计良好且高效的代码。

哲学和编程思想

这段代码体现了多个哲学和编程思想，以下是一些主要的思想：

哲学思想

秩序与结构：哲学上，秩序和结构是宇宙的基本原则。这段代码通过将无序的数字列表转换为有序的螺旋矩阵，体现了对秩序和结构的追求。
简约主义：代码尽量保持简洁和高效，避免不必要的复杂性。这种简约主义的思想在代码的结构和逻辑中得到了体现。

编程思想

模块化：代码被划分为多个函数，每个函数负责一个特定的任务（如输入处理、排序、找到矩阵维度、填充矩阵和输出矩阵）。这种模块化的设计使得代码更易于理解和维护。
抽象化：通过定义 find_dimensions 函数来抽象出找到矩阵维度的逻辑，使得主逻辑更加简洁。这种抽象化的思想有助于隐藏复杂性，提高代码的可读性。
迭代与递归：虽然代码中没有显式的递归，但通过边界指针的迭代方式来填充矩阵，体现了迭代思想。迭代是一种逐步推进的解决问题的方法，适用于处理有序数据。
算法优化：在找到矩阵维度的过程中，代码通过遍历到 sqrt(N) 的整数来减少计算量，体现了算法优化的思想。这种优化减少了不必要的计算，提高了效率。
数据结构选择：代码选择了列表和二维列表（矩阵）作为主要的数据结构，这种选择是基于问题的需求和数据结构的特性。合理选择数据结构是编程中的重要思想。
边界条件处理：在填充矩阵的过程中，代码通过边界指针来控制填充方向，并处理边界条件。这种对边界条件的细致处理是编程中的重要思想，有助于避免错误和提高代码的健壮性。