平衡二叉树定义:二叉排序树的平衡因子绝对值小于等于1,即平衡因子为-1、0、1,那么是平衡二叉树(平衡因子:根结点的左子树深度减右子树深度的差)。
最小不平衡子树:子树的根结点距离插入结点距离最近,且平衡因子绝对值大于1的树为最小不平衡子树。
平衡二叉树:当插入结点后出现最小不平衡子树,那么就要对最小不平衡子树重新构造,通过顺时针(平衡因子皆为正)或逆时针(平衡因子皆为负)旋转最小不平衡子树的根结点使之成为平衡二叉树。注意:如果最小不平衡子树的根结点与页结点不是同号的,需要将其先转为同号再进行上述旋转(如何双旋转:如果最小不平衡树的根结点平衡因子为负数,说明其右子树深度高,为R,结点逆时针旋转;如果最小不平衡树的根结点右子树平衡因子为正数,说明其左子树深度高,为L,结点顺时针旋转;这样就形成了从上往下为RL,则先下子树L旋转,再上子树R旋转;反之为LR旋转)。
我们在处理平衡二叉树的时候回出现4中情况:
LL型单旋转,顺时针旋转(新增结点在最小不平衡子树根的左子树的左子树下,L表示左子树,数字2表示平衡因子)

/**
* 执行LL顺时针旋转,最小不平衡子树才需要旋转,平衡的会过滤,对比图理解会比较容易
* @param tree 不一定是最小不平衡子树,看LR第二个图计算可知
* @return 返回根结点
*/
public TreeNode<T> executeLeftLeft(TreeNode<T> tree) {
TreeNode<T> newRoot;
newRoot = tree.leftSub;
tree.leftSub = newRoot.rightSub;
newRoot.rightSub = tree;
tree.hight = Math.max(getHeight(tree.leftSub), getHeight(tree.rightSub)) + 1;
newRoot.hight = Math.max(getHeight(newRoot.leftSub), getHeight(tree)) + 1;
return newRoot;
}
LR型双旋转,先下后上旋转,先R逆时针选择,后L顺时针旋转(新增结点在最小不平衡子树根的左子树的右子树下,L表示左子树,数字2表示平衡因子)

/**
* 执行LR旋转,则先R逆时针旋转,最后变成LL,再顺时针旋转即可,对比图理解会比较容易
* @param tree 不一定是最小不平衡子树,看LR第二个图计算可知
* @return 返回根结点
*/
public TreeNode<T> executeLeftRight(TreeNode<T> tree) {
tree.leftSub = executeRightRight(tree.leftSub);
return executeLeftLeft(tree);
}
RR型单旋转,逆时针旋转(新增结点在最小不平衡子树根的右子树的右子树下,R表示右子树,数字-2表示平衡因子)

/**
* 执行RR逆时针旋转,最小不平衡子树才需要旋转,平衡的会过滤,对比图理解会比较容易
* @param tree 不一定是最小不平衡子树,看LR第二个图计算可知
* @return
*/
public TreeNode<T> executeRightRight(TreeNode<T> tree) {
TreeNode<T> newRoot;
newRoot = tree.rightSub;
tree.rightSub = newRoot.leftSub;
newRoot.leftSub = tree;
tree.hight = Math.max(getHeight(tree.leftSub), getHeight(tree.rightSub)) + 1;
newRoot.hight = Math.max(getHeight(tree), getHeight(newRoot.leftSub)) + 1;
return newRoot;
}
RL型双旋转,先下后上旋转,先R逆时针选择,后L顺时针旋转(新增结点在最小不平衡子树根的右子树的左子树下,R表示右子树,数字-2表示平衡因子)
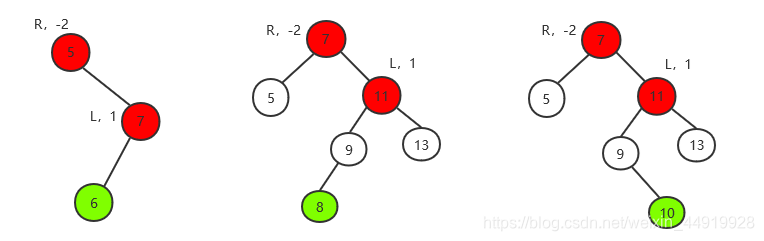
/**
* 执行RL旋转,则先执行L顺时针旋转,最后变成RR,再逆时针旋转即可,对比图理解会比较容易
* @param tree 不一定是最小不平衡子树,看LR第二个图计算可知
* @return
*/
public TreeNode<T> executeRightLeft(TreeNode<T> tree) {
tree.rightSub = executeLeftLeft(tree.rightSub);
return executeRightRight(tree);
}
下面举个栗子具体操作:
依次添加5、4、3、6、10、8、9、14、13这些结点
(1)前面添加到3时才会不平衡,因此就从添加3开始了,加3后,LL,根顺时针单旋转

(2)加6后任然是平衡树

(3)加10后,RR,最小不平衡树根逆时针单旋转
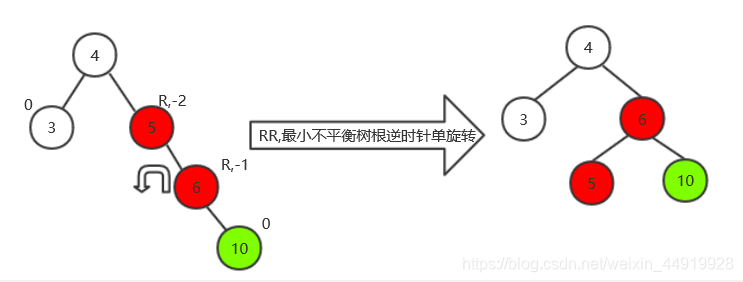
(4)加8后RR,最小不平衡树根逆时针单旋转

(5)加9后LR,所以先R逆时针旋转后L顺时针旋转








 本文详细介绍了AVL树的概念,包括平衡因子、最小不平衡子树和四种旋转操作(LL、LR、RR、RL)。通过实例展示了在节点插入过程中如何维护平衡,确保树的平衡因子保持在-1、0、1之间。
本文详细介绍了AVL树的概念,包括平衡因子、最小不平衡子树和四种旋转操作(LL、LR、RR、RL)。通过实例展示了在节点插入过程中如何维护平衡,确保树的平衡因子保持在-1、0、1之间。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 865
865

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








