熄灯问题（枚举）——C++

最新推荐文章于 2025-02-25 13:36:38 发布

啊哈嗯嗯

最新推荐文章于 2025-02-25 13:36:38 发布

阅读量2.7k

点赞数 4

文章标签：算法 c++

本文链接：https://blog.csdn.net/weixin_44937336/article/details/104196805

版权

本文介绍了一种解决灯矩阵灭灯问题的算法，通过枚举第一行按钮状态，利用异或运算确定后续按钮状态，确保所有灯熄灭。文章详细解释了算法原理，包括状态枚举、按钮状态确定及灯熄灭条件判断。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述
有一个由按钮组成的矩阵，其中每行有6个按钮，共5行。每个按钮的位置上有一盏灯。当按下一个按钮后，该按钮以及周围位置(上边、下边、左边、右边)的灯都会改变一次。即，如果灯原来是点亮的，就会被熄灭；如果灯原来是熄灭的，则会被点亮。在矩阵角上的按钮改变3盏灯的状态；在矩阵边上的按钮改变4盏灯的状态；其他的按钮改变5盏灯的状态。

请你写一个程序，确定需要按下哪些按钮，恰好使得所有的灯都熄灭。根据上面的规则，得：
1）第2次按下同一个按钮时，将抵消第1次按下时所产生的结果。因此，每个按钮最多只需要按下一次；
2）各个按钮被按下的顺序对最终的结果没有影响；
3）对第1行中每盏点亮的灯，按下第2行对应的按钮，就可以熄灭第1行的全部灯。如此重复下去，可以熄灭第1 ~ 4行的全部灯。同样，按下第1 ~ 5列的按钮，可以熄灭前5列的灯。

输入数据
输入由5行组成，每一行包括6个数字（0或1）。相邻两个数字之间用单个空格隔开。0表示灯的初始状态是熄灭的，1表示灯的初始状态是点亮的。

输出要求
输出由5行组成，每一行包括6个数字（0或1）。相邻两个数字之间用单个空格隔开。其中的1表示需要把对应的按钮按下，0则表示不需要按对应的按钮。

样例输入

0 1 1 0 1 0
1 0 0 1 1 1
0 0 1 0 0 1
1 0 0 1 0 1
0 1 1 1 0 0

样例输出

1 0 1 0 0 1
1 1 0 1 0 1
0 0 1 0 1 1
1 0 0 1 0 0
0 1 0 0 0 0

解题思路：

如何枚举？
因为灯有30盏，按钮有开关两种状态，如果一次性枚举需要的次数为2³⁰,明显复杂度太大。但是，我们知道第一行的灯是由第一行的按钮得状态和第二行的按钮的状态确定，就是说，如果第一行的按钮的状态确定后，那么相续的第二行的按钮的状态也确定了。因此我们只需要枚举第一行的按钮的状态就可以了，枚举次数为2⁶ = 64。

如何确定按钮的状态？
因为一盏灯被按钮开关两次后其灯的状态不变，那么确定一个按钮的状态时可以用异或的方式实现。即：
ans[i][j] = block[i-1][j] ^ ans[i-1][j] ^ ans[i-1][j-1] ^ ans[i-1][j+1] ^ ans[i-2][j]

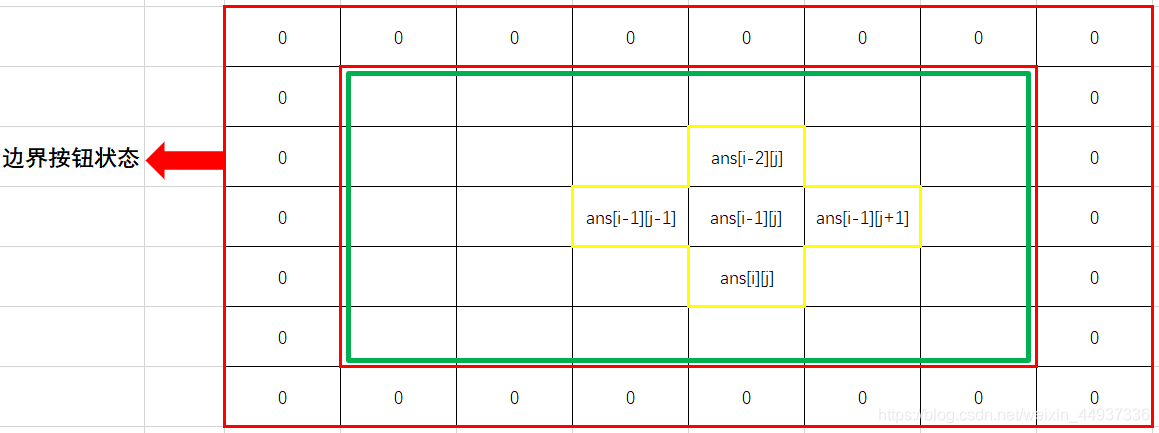
在这里插入图片描述

如何判断是否熄灭全部的灯？
当第五行的按钮的状态确实能够后，如果没有关闭到第四行或第五行的灯，由
ans[6][j] = block[5][j] ^ ans[5][j] ^ ans[5][j-1] ^ ans[5][j+1] ^ ans[4][j] 可知，将需要由第6行（边界按钮）的按钮来关闭，即会改变第6行的值，将 0 变为 1 。那么可以用 if(ans[6][j] == 1) 来判断。

如何枚举第一行的按钮的状态？
把这一行的6个按钮比喻为6位的二进制数，即000000 ~ 111111 。
把这64种情况一一枚举，直至匹配成功。

0 0 0 0 0 0 
0 0 0 0 0 1
0 0 0 0 1 0
0 0 0 0 1 1
0 0 0 1 0 0
0 0 0 1 0 1
	.
  . . . 
  	.
1 1 1 1 1 1

#include<iostream>
using namespace std;
int ans[7][8] , block[6][7];
bool check()
{
	for(int i=2;i<=6;i++)
	{
		for(int j=1;j<=6;j++)
		{
			ans[i][j] = block[i-1][j] ^ ans[i-1][j] ^ ans[i-1][j-1] ^
					    ans[i-1][j+1] ^ ans[i-2][j];
		}
	}
	for(int j=1;j<=6;j++)
		if(ans[6][j] == 1)
			return false;
	return true;
}

void solve()
{
	for(int i=0;i<64;i++)  //枚举64次
	{
		int k = i;
		for(int j=6;j>=1;j--)
		{
			ans[1][j] = k%2; //变为二进制
			k/=2;
		}
		if(check())
			break;
	}
	for(int x=1;x<=5;x++)
	{
		for(int y=1;y<=6;y++)
		{
			cout<<ans[x][y]<<" ";
		}
		cout<<endl;
	}
}

int main()
{
	for(int i=0;i<8;i++)
		ans[0][i]=ans[6][i]=0; // 确定边界按钮状态
	for(int j=1;j<6;j++)
		ans[j][0]=ans[j][7]=0; // 确定边界按钮状态

	for(int x=1;x<=5;x++)
		for(int y=1;y<=6;y++)
			cin>>block[x][y];
	cout<<"\n"<<"\n";
	solve();
return 0;
}