运动模糊图像复原模型PSF

运动模糊图像复原模型PSF

• 目的及用途

通过估计运动模糊参数，利用运动模糊图像复原模型，实现对运动模糊图像的复原。

运动模糊，顾名思义，就是在场景中发生运动的物体在场景拍摄曝光时所产生的模糊效果。

运动模糊现象出现的原因：物体和相机的相对运动。

例如：疾驰的汽车、田径场上的短跑运动员。

• 算法概述

1. 算法原理

PSF是Point Spread Function，点扩散函数，即点光源经过系统后形成的光斑。即便是没有像差的理想系统，由于孔径带来的衍射因素，点光源也不能汇聚成一个无穷小的点，只能“散成一滩”PSF。

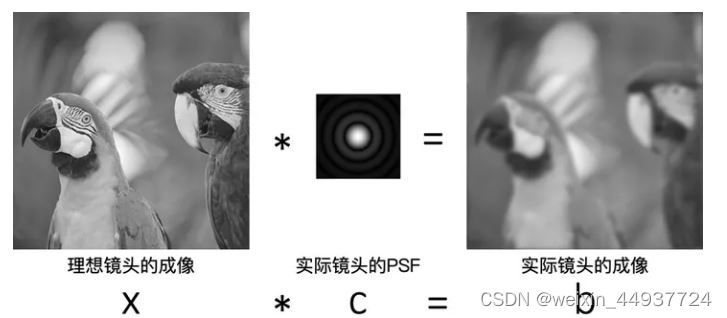
假设有一个理想镜头，不受衍射的影响，用它所成的像为x，而实际镜头的PSF为c，实际镜头的成像是b，那么这三者之间的关系是一种典型的卷积关系：

根据实际镜头的成像b，以及镜头的PSF，获取理想的成像x。

1. 预备知识

（1）卷积

空域的卷积相当于频域的乘法；

去卷积相当于在频域上做除法；

对除法的结果做反傅里叶变换就可以得到去卷积的结果。

（2）Radon变换

（3）二维傅里叶变换

1. 运动模糊图像退化模型

对模糊图像进行复原的关键是建立图像的退化模型，在考虑噪声的情况下，图像的退化模型可近似用统一的线性模型表示为

gx,y=fx,y*hx,y+nx,y                                           (1)

式中，gx,y为退化图像；hx,y为退化函数；fx,y为原始图像；nx,y为随机噪声函数；*为卷积。

对式（1）进行傅里叶变换则有

Gu,v=Fu,vHu,v+Nu,v                                               (2)

式中，Gu,v，Fu,v，Hu,v，Nu,v分别为式（1）各函数的傅里叶形式。

原图像fx,y通过退化函数PSF影响退化后的图像为gx,y，求解PSF是复原模糊图像的核心问题。

由于变速与非直线运动都可分解为各段的匀速直线运动，所以，研究匀速直线运动产生的运动模糊具有普遍意义，PSF由下式表示

hx,y=1L,0≤x≤Lcosθ,0≤y≤xtanθ0,                                               otherwise                      (3)

式中，θ为物体运动方向与水平方向之间的夹角，称为运动模糊角度，L为运动方向上像素移动的距离，称为运动模糊尺度。得知运动模糊角度θ与运动模糊尺度L，便可求解PSF，进而进行运动模糊图像复原。

1. 算法输入、输出

1. 输入：实际图像、运动模糊角度θ、运动模糊尺度L
2. 输出：复原后的图像

1. 算法参数

1. 运动模糊角度θ
2. 运动模糊尺度L

• 算法步骤

参考运动模糊恢复_restoration of blurred, noisy image using estimate_NineDays66的博客-CSDN博客

1. 主要步骤

1. 估计运动模糊参数，得到PSF

运动模糊角度θ的估计：常见的辨识方法有频域法和倒谱法；

频域法的原理是将退化图像进行二维傅里叶变换，得到具有相互平行的规则明暗条纹的频谱。设暗纹与x轴正向夹角为φ，运动模糊方向与x轴夹角为θ，图像尺寸为M×N,根据傅里叶变换的时频特性可以知道，可通过公式tan(θ)=tan(φ-90°)×MN，得到模糊角度θ,因此只要通过Radon变换检测出频谱暗条纹与水平方向的夹角即可得到运动模糊方向。

预备知识-二维傅里叶变换：

一维傅里叶变换的公式为Fω=-∞+∞f(x)e-jωxdx，通俗来讲，一维傅里叶变换是将一个一维的信号分解成若干个复指数波。而由于ejωx=cos(ωx)+jsin(ωx)，所以可以将每一个复指数波ejωx都视为是余弦波与正弦波的组合。

类似的，二维傅里叶变换的公式为Fu,v=-∞+∞-∞+∞f(x,y)e-j2π(ux+vy)dxdy，将一个图像分解成若干个复平面波ej2π(ux+vy)之和，一维傅里叶变换与二维傅里叶变换示意图如图1所示，图像的二维傅里叶变换如图2所示。

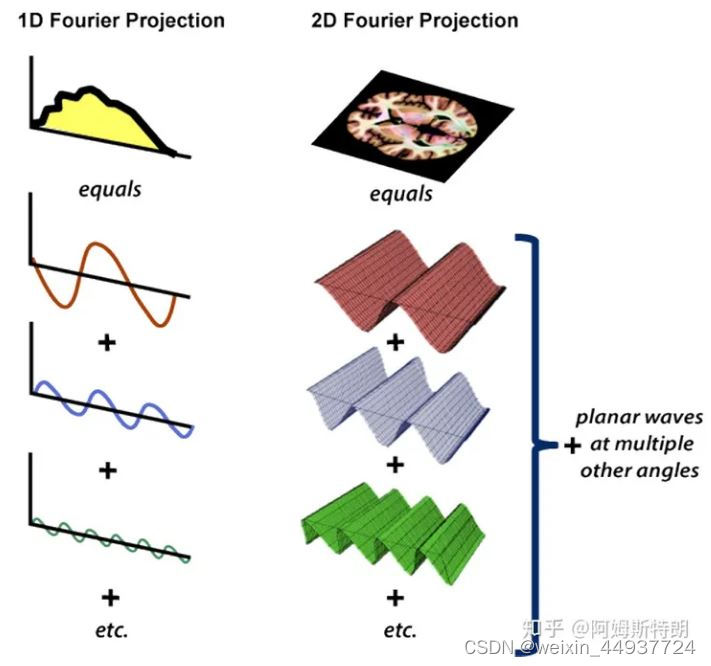
图1 一维傅里叶变换与二维傅里叶变换示意图

  

图2 图像的二维傅里叶变换

原图水平方向上变化更多，是水平方向上的运动模糊（其相间条纹是竖直的），所以频谱图水平方向更亮。竖直方向变化比水平方向少，所以较水平方向暗。

沿着模糊运动方向变化更多，对应的频谱图上模糊运动方向更亮，只要通过Radon变换检测出频谱暗条纹与水平方向的夹角即可得到运动模糊方向。

倒谱法的主要原理是先将退化图像进行二维傅里叶变换，然后取对数，再进行反傅里叶变换得到退化图像的倒频谱,分离出退化图像的模糊信息，进而通过Radon变换得到运动模糊方向。

Radon变换是对频谱图上某一指定角度进行线积分，通过计算1°~180°的Radon变换得到180列的矩阵R，每一列向量是图像在一个角度上沿一簇直线的积分投影，因为积分直线束与频谱中的亮暗条纹平行，所以所得的投影向量中应有一个最大值，在频域法中最大值所对应的列数就等于模糊方向与x轴正方向水平夹角；在倒谱法中，最大值对应的列数±90°即为所求的运动模糊角度。

运动模糊尺度L的估计：

可以沿运动方向对模糊图像求方向导数,得到一正一负两个原始图像的叠加像,两者的距离就是模糊尺度。

根据倒频谱负峰值距离估计出模糊尺度。

1. 对退化图像gx,y、PSF（hx,y）、随机噪声函数nx,y分别进行傅里叶变换，得到Gu,v、Hu,v、Nu,v
2. 根据式（2），计算原始图像的傅里叶变换Fu,v
3. 对Fu,v进行傅里叶逆变换，获得原始图像（复原后的图像）。

• 算法优缺点

1. 优点：利用退化过程的先验知识使已退化的图像恢复本来面目。
2. 缺点：

1. 估计误差大、有效估计范围有限
2. 对整幅图像进行全局的复原：由于物体运动而产生的相对运动，其运动模糊只出现在物体运动的轨迹上，而背景是清晰的，在这种情况下就不能对全局进行处理。
3. 利用Radon变换直接求取模糊尺度存在一定的缺点，当模糊图像中含有的噪声强度较大时，其频谱图的暗条纹会变得模糊不清。

• 改进方向

1. 分块复原时局部图像块的大小

根据图像的整体模糊特征确定局部图像块的大小，对每个局部图像块分别进行复原。

1. 运动模糊参数的估计

对于全局模糊（即由于镜头运动导致模糊）的图像，先将图像进行分块，找出最能代表原始模糊图像模糊特征的子图像块，仅仅根据最具代表性的子图像块估计运动模糊参数，减少计算量。

对于局部模糊（即由于物体运动导致模糊）的图像，先获取物体运动区域，仅对物体运动区域进行复原。

（参考论文《基于改进PSF估计的车载复杂图像复原》）

场景分析，在汽车的行驶过程中，摄像头相对于背景发生运动，并且在背景图像中，其它物体也有相对运动。

主要思想：

1. 先求出全局运动模糊核，对图像进行全局模糊恢复，去除全局运动模糊；

在模糊图像块的频谱图中，亮暗条纹相间，可通过相间的条纹的角度来计算出模糊角度，一般使用Radon变换来估算出方向。模糊图像的像素点具有很强的相关性，像素点的灰度值逐渐变化，因此可通过模糊图像的自相关函数图求得模糊尺度。

1. 再结合图像的局部均方差和结构相似度来判断图像块是否模糊，分割出局部模糊区域，对其进行复原；

局部均方差：当图像模糊时，图像相邻间的像素关联性较强、变化缓慢，从而均方差也较小。因此对于模糊失真的图像比较敏感，可用均方差来比较两幅图像是否模糊。

结构相似度：亮度、对比度和结构。

1. 最后合成清晰的图像