C++排序算法总结

最新推荐文章于 2024-04-25 12:18:13 发布
置顶 最新推荐文章于 2024-04-25 12:18:13 发布
阅读量567 收藏 3
点赞数
文章标签： c++ 排序算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_44974029/article/details/119647004
版权

1.蛮力冒泡排序

冒泡排序与选择排序是用蛮力法解决排序问题的最直观的例子。
冒泡排序法(Bubble Sort)是由观察水中冒泡现象而来。如果将待排序的元素值看作是质量，那么，质量小的元素应向水面上浮（即向左边移动）。
冒泡排序的基本思想是：两两比较相邻记录，如果反序则交换，直到没有反序的记录为止。

#include<iostream>
#include<iomanip>
using namespace std;
//数组输出
void Display(int* data, int n)
{
	for (int i = 0; i < n; i++)
		cout << setw(3) << data[i];
	cout << endl;
}
void Bubble(int* data, int n)
{
	for (int i = 1; i < n; i++)//做第i=1,2,...,n-1趟排序
	{
		for (int j = n - 1; j > i - 1; j--)
		{
		//i=1时
		//4		5	3	6	2	1
		//					j-1	j
		//...
		//j-1	j
		//由上述过程可以得出循环介绍的条件是j>i-1
			if (data[j] < data[j - 1])
			{//交换
				int temp = data[j];
				data[j] = data[j - 1];
				data[j - 1] = temp;
			}
		}
		//显示第i趟排序后的数组
		cout << "第" << setw(2) << i << "趟排序 "; Display(data, n);
	}
}
//主函数
int main()
{	int data[6]={4,5,3,6,2,1};//待排序数组
	cout<<"待排序数组 ";Display(data,6);
	Bubble(data,6);//调用冒泡排序函数
	return 0;
}

运行结果如下图1.1。
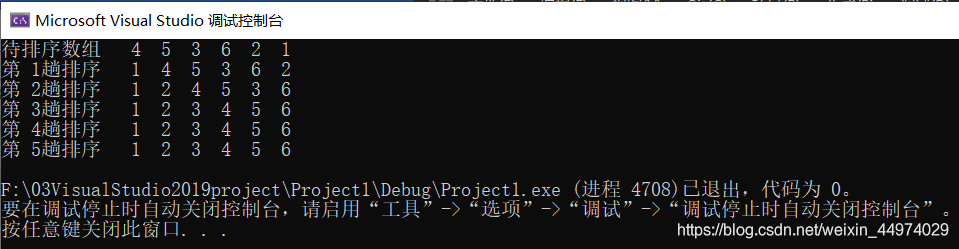在这里插入图片描述对6个元素做冒泡排序，在最坏情况下，需要做5趟排序。由上图发现，该数组其实只需做3趟排序即可，后面的两趟排序是多余的。为了克服这一缺陷，只需在冒泡函数中，增加一个标识变量和一个判断语句，就可弥补此缺陷，使臻完善。

//冒泡排序
void Bubble(int* data, int n)
{
	int flag;
	for (int i = 1; i < n; i++)//做第i=1,2,...,n-1趟排序
	{
		flag = 1;//先假设数组为正序
		for (int j = n - 1; j > i - 1; j--)
		{
			if (data[j] < data[j - 1])
			{
				flag = 0;//数组中仍有逆序
				int temp = data[j];
				data[j] = data[j - 1];
				data[j - 1] = temp;
			}
		}
		if (flag == 1)//如果做完第i趟排序发现数组确为正序
			break;//退出,不必输出结果,也不再参与后续排序
		else
		{	//显示第i趟排序后的数组
			cout << "第" << setw(2) << i << "趟排序 "; Display(data, n);
		}
	}
}

用改进后的冒泡函数去置换上述程序中的冒泡函数，程序运行结果如下图1.2。
在这里插入图片描述对冒泡排序法的性能分析：
n 个元素用冒泡排序法来排序，最好情况（已有序）下只需做一趟排序，做 n-1次元素比较，因此最好情况下的时间复杂度为O(n) ，无须移动元素；最坏情况下需做n-1 趟排序，第 i趟的元素比较n-i 次，移动元素 3(n-i)次，总的比较次数为1/2n(n-1)、移动次数为3/2n(n-1),因此，在最坏情况下的时间复杂度为 O(n*n)。
该算法执行时间与元素的初始排列有关，冒泡排序经过一趟排序后，能确定一个元素的最终位置。由图1.2可以看出，当待排序序列基本有序时，可以减少排序趟数。这表明，冒泡排序“偏爱”基本有序的序列。由于冒泡排序中的元素交换是相邻元素的交换，因此，冒泡排序是稳定的排序方法。冒泡排序仅需一个额外的存储空间用来存放变量temp。

2.蛮力选择排序

选择排序法（Select Sort）是在待排序序列data[0]—data[n-1]中，找出最小值元素，将它与data[0]交换，然后再待排序子序列data[1]—data[n-1]中，再找出最小值元素，再将它与data[1]交换，如此做下去，经过n-1趟排序后，使得待排序序列成为有序序列。

#include<iostream>
#include<iomanip>
using namespace std;
//输出数组
void Display(int* data, int n)
{
	for (int i = 0; i < n; i++)
		cout << setw(3) << data[i];
	cout << endl;
}
//选择排序
void Select(int* data, int n)
{
	int min, pos, flag;
	for (int i = 1; i < n; i++)//做第i=1,2,...,n-1趟排序
	{	//用顺序搜索法找出data[i-1]至data[n-1]的最小值
		min = data[i - 1];
		pos = i - 1;
		flag = 1;//先假设data[i-1]为最小值
		for (int j = i; j < n; j++)
		{
			if (min > data[j])
			{
				min = data[j];
				pos = j;
				flag = 0;//data[i-1]并非最小值,flag置0
			}
		}
		if (flag == 0)//如果最小值被改变
		{	//做交换
			int temp = data[i - 1];
			data[i - 1] = data[pos];
			data[pos] = temp;
		}
		//显示第i趟排序后的数组
		cout << "第" << setw(2) << i << "趟排序 "; Display(data, n);
	}
}
//主函数
int main()
{
	int data[6] = { 4,5,3,6,2,1 };//待排序数组
	cout << "待排序数据 "; Display(data, 6);
	Select(data, 6);//调用选择排序函数
	return 0;
}

运行结果如下图2.1
对选择排序法的性能分析：
对任意初始数据，该算法都必须执行n-1趟。第i趟执行n-i次比较，这样总的比较次数为1/2n(n-1)。 因此，选择排序的最好、最坏和平均情况的时间复杂度都为***O(nn) ，而且它还需交换元素n-1次和移动元素3(n-1)次。
该排序算法经过一趟排序后，能确定一个元素的最终位置。由于元素间的交换不一定是相邻元素的交换，因此它是不稳定的。选择排序仅需一个额外的存储空间用来存放变量temp。由于该排序法在最好、最坏和平均情况下的时间复杂度都一样，它适合对那些“杂乱无序”数据进行排序。

3.减治插入排序

插入排序数据减治法的减一技术。
插入排序法(Insert Sort)是将序列中第一个元素作为一个有序序列，然后将剩下的 个元素按大小依次插入该有序序列，每插入一个元素后依然保持该序列有序。

#include<iostream>
#include<iomanip>
using namespace std;
//输出数组
void Display(int* data, int n)
{
	for (int i = 0; i < n; i++)
		cout << setw(3) << data[i];
	cout << endl;
}
//插入排序
void Insert(int* data, int n)
{
	for (int i = 1; i < n; i++)//做第i=1,2,...,n-1趟排序
	{
		int temp = data[i];// temp暂存待插元素
		int j = i - 1;//确定待插元素的前驱位置
		while (j >= 0 && temp < data[j])//当待插元素值小于它的前驱值时
		{
			data[j + 1] = data[j];//前驱元素后移
			j--;//前驱位置前移
		}
		data[j + 1] = temp;//找到temp的插入位置,使它归位
		//显示第i趟排序后的数组
		cout << "第" << setw(2) << i << "趟排序 "; Display(data, n);
	}
}
//主函数
int main()
{
	int data[6] = { 4,5,3,6,2,1 };//待排序数组
	cout << "待排序数组 "; Display(data, 6);
	Insert(data, 6);//调用插入排序函数
	return 0;
}

运行结果如下图3.1
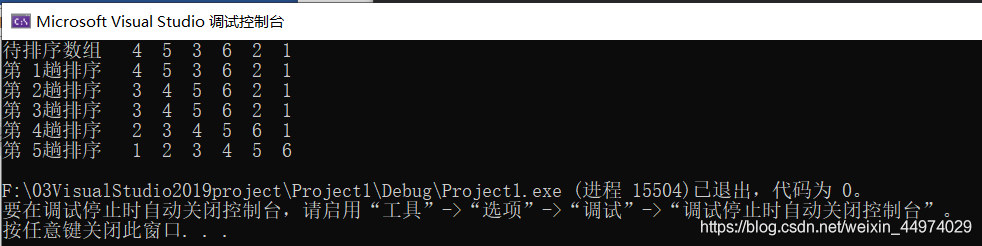在这里插入图片描述对插入排序法的性能分析：
插入排序法必须进行n-1趟。最好情况（初始序列为升序的）下，执行n-1趟排序，每趟比较1次，总的比较次数为 n-1，因此最好情况下的时间复杂度为O(n) 。
最坏情况（初始序列为降序的）下，第i趟排序，比较次数为 i次，移动元素次数2i次，需要的比较次数和移动元素次数分别为1/2n(n-1)，n*(n-1)，因此最坏情况下的时间复杂度为 O(n*n)。
在第i趟排序中，是将元素data[i]与i个有序元素data[0],…,data[i-1]调整成有序的，仅在data[i]<data[j]（0≤j≤i-1）时，才会依序移动元素，故它是稳定的。且只需一个额外的存储空间用来存放变量temp。由于该排序法在最好、最坏情况下的时间复杂度相差甚大，因此它适宜对基本有序的数据进行排序。
除了冒泡、选择和插入这三种基本排序法外，还有一些排序效率更高的排序法。

4.减治堆排序

堆排序法是选择排序法的一种改进，它可以减少选择排序法中的比较次数，进而提高排序效率。堆排序法利用最大堆（或最小堆）来完成排序。

#include<iostream>
#include<iomanip>
using namespace std;
//输出函数
void Display(int *data,int n)
{	for(int i=0;i<n;i++)
		cout<<setw(2)<<data[i];
	cout<<endl;
}
//下滑法调最大堆
void SiftDown(int *data,int n)
{	//将data[0]-data[n-1]调成最大堆
	int i,j,temp,parent;
	for(parent=(n-2)/2;parent>=0;parent--)
	{	i=parent;
		temp=data[i];//temp取双亲结点值
		j=2*i+1;//让j指向i的左孩子位置
		while(j<n)
		{	if(j+1<n) //如果右孩子位置j+1未超界
				j=data[j]<data[j+1]?j+1:j;//让j指向左右孩子中最大者的位置
			if(temp>data[j])//如果双亲结点值大
				break;//不做交换
			else//如果双亲结点值小
			{	data[i]=data[j];//做交换
				i=j;//改变双亲结点位置
				j=2*i+1;//再让j指向i的左孩子位置
			}
		}
		data[i]=temp;//使temp归位
	}
}
//堆排序
void HeapSort(int *data,int n)
{	int i,temp;
	for(i=1;i<n;i++)//做第i=1,...,n-1趟排序
	{	//用下滑法将data[0]-data[n-i]将调成最大堆
		SiftDown(data,n-i+1);
		//头尾结点交换
		temp=data[n-i];
		data[n-i]=data[0];
		data[0]=temp;
		//输出第i趟排序结果
		cout<<"第"<<setw(2)<<i<<"趟排序 ";
		Display(data,n);
	}
}
//主函数
int main()
{	int data[7]={5,2,6,1,7,3,4};//待排序数组
	cout<<"待排序数据 ";Display(data,7);
	HeapSort(data,7);//调用堆排序函数
	return 0;
}

运行结果如下图4.1
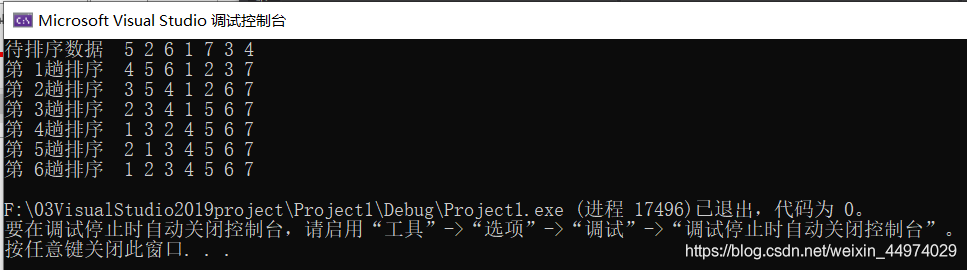在这里插入图片描述对堆排序法的性能分析：
在所有情况下，堆排序法的时间复杂度为 O(n*log2n)，堆排序是不稳定的，只需要一个额外的存储空间。

5.分治快排

分治法（divide and conquer method）是著名算法设计技术之一。用计算机求解问题时所需的时间一般都与问题规模有关。问题规模越小，求解问题所需的时间也越少，从而也较容易处理。
分治法将一个难以直接解决的大问题划分成一些规模较小的子问题，分别求解各个子问题，再合并子问题得到原问题的解。
快速排序算法的思想就是分治法。快速排序法是目前公认的最佳排序法，它是采用递归方式进行排序的。
快排算法首先对排序序列进行划分，划分的基准元素应该遵循平衡子问题的原则，使划分后的两个子序列的长度尽可能相等，这是决定快排算法时间性能的关键。基准的选择可以由很多种，例如可以随机选出一个记录作为基准元素。

#include<iostream>
#include<iomanip>
using namespace std;
//输出函数
void Display(int* data, int n)
{
	for (int i = 0; i < n; i++)
		cout << setw(3) << data[i];
	cout << endl;
}
//快速排序算法
void QuickSort(int a[], int left, int right)
{
	if (left > right)
		return;
	int static cnt = 0;//快速排序趟数统计变量
	int k = a[left];//k存放基准元素
	int i = left;
	int j = right;
	while (i != j)
	{
		while (a[j] >= k && i < j)//从左往右找比k小的元素位置
			j--;
		while (a[i] <= k && i < j)//从右往左找比k大的元素位置
			i++;
		//交换两个元素在数组中的位置
		if (i < j)//当i和j不相遇
		{
			int temp = a[i]; a[i] = a[j]; a[j] = temp;
		}
	}
	a[left] = a[i]; a[i] = k;//与a[i]与基准元素k交换
	//显示第i趟排序后的数组
	cout << "第" << setw(2) << ++cnt << "趟排序 "; Display(a, 7);
	QuickSort(a, left, i - 1);//继续处理左边的序列
	QuickSort(a, i + 1, right);//继续处理右边的序列

}
//主函数
int main()
{
	int data[7] = { 5,2,6,1,7,3,4 };//待排序数组
	cout << "待排序数组 ";Display(data, 7);
	QuickSort(data, 0, 6);
	return 0;
}

运行结果如下图5.1
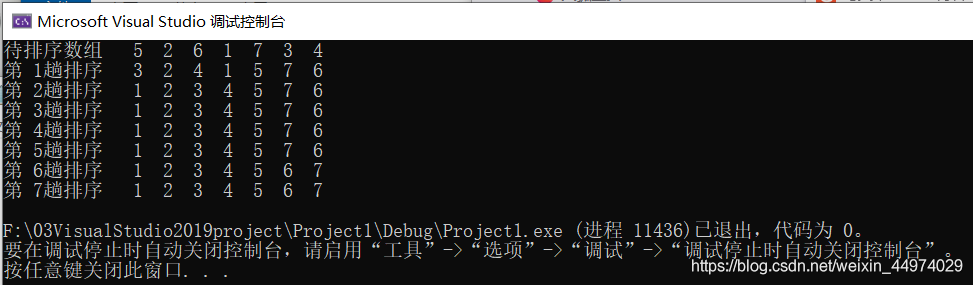在这里插入图片描述对快速排序法的性能分析：
在最好和平均情况下，时间复杂度为O(n*log2n)。最坏情况下的时间复杂度为O(n*n) 。快速排序法是不稳定的排序法。空间复杂度在最坏情况下为 O(n)，在最好情况下为O(log2n) 。

6.分治归并

二路归并排序是成功应用分治法的一个完美例子。
下面，介绍二路归并排序思想。
将待排序数组视为有序数组。
第1趟：从左至右按len=1分组，将它们合并为长度len=2的有序数组；
第2趟：从左至右按len=2分组，并将它们合并为长度len=4的有序数组；
第3趟：从左至右按len=4分组，并将它们合并为长度len=8的有序数组。
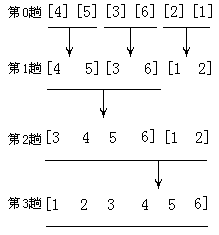
在这里插入图片描述
具体实现过程，如下图所示：
在这里插入图片描述其中，DividMerge(a,n,len)表示对含n个元素数组a按长度len进行分组。Merge(a,left,mid,right)表示对有序左段a[left,mid]与有序右段a[mid+1,right]进行合并

#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
#define N 6
//输出函数
void Display(int a[],int n)
{
	int i,col=0;
	for(i=0;i<n;i++)
	{
		cout<<setw(6)<<a[i];
		col++;
		if(col==20)
		{
			cout<<endl;
			col=0;
		}
	}
	cout<<endl;
}

//2段归并
void Merge(int a[],int left,int mid,int right)
{
	//归并 有序左段a[left...mid]与有序右段a[mid+1...right]
	int *A;//定义一个动态数组
	A=new int[right-left+1];//为A分配内存 
	int i=left,j=mid+1,k=0;//k为A的首下标
	while(i<=mid&&j<=right)
	{
		if(a[i]<a[j])
		{
			A[k]=a[i];//将有序左段元素存入A
			i++;k++;
		}
		else
		{
			A[k]=a[j];//将有序右段元素存入A
			j++;k++;
		}
	}
	while(i<=mid)//将有序左段余下元素存入A 
	{
		A[k]=a[i];
		i++;k++;
	}
	while(j<=right)//将有序右段余下元素存入A
	{
		A[k]=a[j];
		j++;k++;
	}
	for(k=0,i=left;i<=right;k++,i++)//使a=A
		a[i]=A[k];
}
//分组归并
void DividMerge(int a[],int n,int len)
{
	int i;
	for(i=0;i+2*len-1<n;i=i+2*len)//合并长度为len的两相邻数组
		Merge(a,i,i+len-1,i+2*len-1);//相邻两数组归并
	if(i+len-1<n)//余下的两个数组,后者长度小于len
		Merge(a,i,i+len-1,n-1);//余下两数组归并
	//显示本趟分组排序后的数组
	cout<<"第"<<setw(2)<<log(len)/log(2)+1<<"趟排序 ";
	Display(a,n);
}
//二路归并排序
void MergeSort(int a[],int n)
{
	int len;//分组长度
	for(len=1;len<n;len=2*len)
		DividMerge(a,n,len);//分组
}
//主函数
void main()
{
	int a[N]={4,5,3,6,2,1};
	cout<<"待排序数组 ";Display(a,N);
	MergeSort(a,N);//合并排序
}

运行结果如图6.1
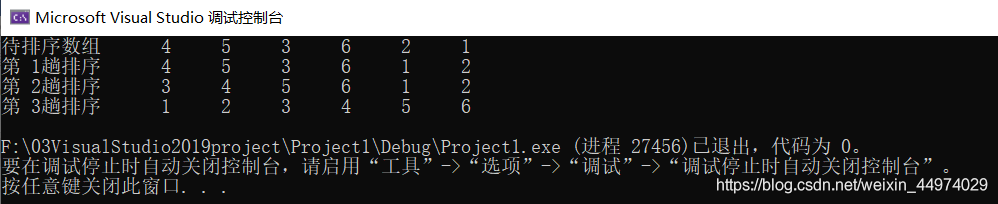在这里插入图片描述由算法可知，需要一个与待排序数组a[]等长的辅助数组A[]，故空间复杂度为O(n)。
待排序数组含 个元素，将此 个元素看作叶子结点，若将两两归并生成的数组看作它们的父结点，则归并过程对应由叶向根生成一棵二叉树的过程。所以归并趟数约等于二叉树的高度减1，约为log2n，每趟归并大约需移动元素n次，故时间复杂度为O(n*log2n)。它不随待排序数组的初始状态的变化而变化，它是稳定的排序法。
快速排序也是基于分治法的排序算法。与二路归并排序不同的是，二路归并排序是按照元素在序列中的位置，对序列进行分组划分。而快速排序是按照元素的值，对序列进行分组划分。

7.桶排序

基数排序法又称桶排序（Bucket Sort），是利用对多关键字进行排序的思想，实现对单关键字进行排序的方法。
基数排序法可分最高位优先MSD(Most Significant Digit First)和最低位优先LSD(Least Significant Digit First)两种。MSD法是从最左边的位数开始比较，而LSD则是从最右边的位数开始比较。
下面，采用低位优先法，对数组data[12]={59,95,7,34,60,168,171,259,372,45,88,133}进行升序排序。
（1）根据初始数据次序，按数据的个位数字，放入相应编号的桶中。数据按个位数字进桶后的状态如下表所示。
在这里插入图片描述依个位数字排序后的数据次序如下：
60 171 372 133 34 95 45 7 168 88 59 259
（2）再根据个位数字排序后的数据次序，按数据的十位数字，再放入相应编号的桶中。数据按十位数字进桶后的状态如下表所示。
在这里插入图片描述依十位数字排序后的数据次序如下：
7 133 34 45 59 259 60 168 171 372 88 95
（3）再根据十位数字排序后的数据次序，按数据的百位数字，再放入相应编号的桶中。数据按百位数字进桶后的状态如下表所示。
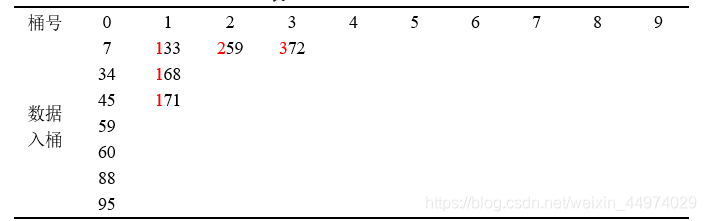
在这里插入图片描述
依百位数字排序后的数据次序如下：
7 34 45 59 60 88 95 133 168 171 259 375
上述对桶排序过程的描述，可提炼成以下程序中的桶排序函数BucketSort。
核心三步：一、获取个，十，百，并初始化桶。二、进桶。三、出桶，并输出桶状态和数组状态。

#include<iostream>
#include<iomanip>
using namespace std;
//输出函数
void Display(int *data,int n)
{	for(int i=0;i<n;i++)
		cout<<setw(5)<<data[i];
	cout<<endl;
}
//初始化桶
void Initial(int *bucket,int n)
{	for(int j=0;j<10;j++)
	{	bucket[0*10+j]=j;//第0行为桶号(0-9)
		for(int i=1;i<n+1;i++)
			bucket[10*i+j]=0;//第1-n行置0,表示桶空
	}
}
//桶排序
void BucketSort(int *data,int *bucket,int n)
{	int i,j,p,q;
	for(p=1;p<=100;p=p*10)//基数p分别取1,10,100
	{	Initial(bucket,n);//初始化桶
		int row[10]={0};//row[]记录0-9号桶内装入数据个数
		//data进桶
		for(i=0;i<n;i++)
		{	q=(data[i]/p)%10;//p=1,q取个数,p=10,q取十位,p=100,q取百位
			row[q]++;//q号桶装入数据个数增1
			bucket[10*row[q]+q]=data[i];//data[i]进入q号桶
		}
		//搜索桶中装入元素个数的最大值
		int MaxRow=0;
		for(j=0;j<10;j++)
		{	if(row[j]>MaxRow)
				MaxRow=row[j];
		}
		//按p位排序结果改写数组data
		int k=0;//活动下标
		for(j=0;j<10;j++)
			for(i=1;i<=MaxRow;i++)
				if(bucket[10*i+j]!=0)
					data[k++]=bucket[10*i+j];
		//输出桶状态
		cout<<setw(3)<<p<<"位进桶状态"<<endl;
		for(i=0;i<=MaxRow;i++)
		{	for(j=0;j<10;j++)
				cout<<setw(5)<<bucket[10*i+j];
			cout<<endl;
		}
		//输出p位排序后的数组
		cout<<setw(3)<<p<<"位排序 ";Display(data,n);
	}
}
//主函数
int main()
{	int data[12]={59,95,7,34,60,168,171,259,372,45,88,133};
	int *bucket=new int(13*10);//桶数组
	cout<<"  初始数组 ";Display(data,12);
	BucketSort(data,bucket,12);
	return 0;
}

运行结果如图7.1
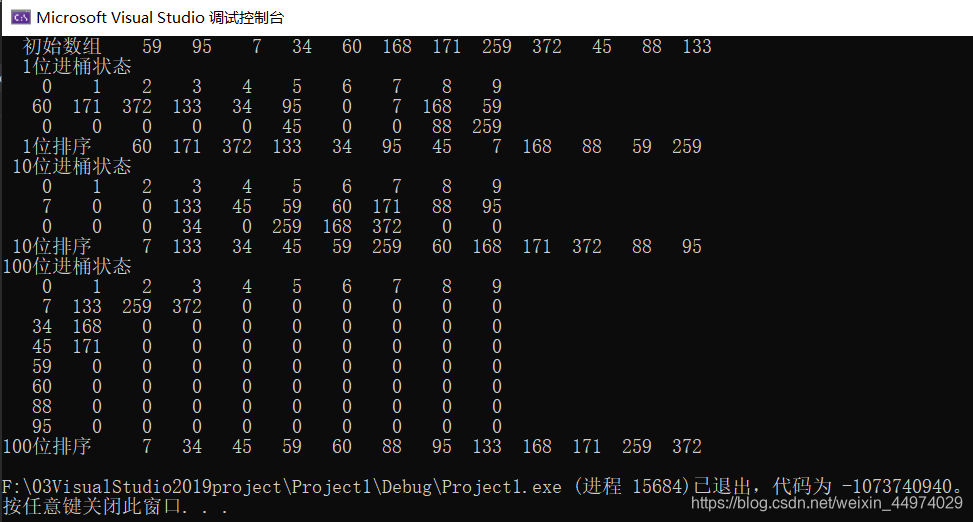在这里插入图片描述对桶排序法的性能分析：
在所有情况下，基数排序法的时间复杂度O(n)、空间复杂度均为O(n) ，它是稳定的，当n很大时，此排序法拥有极高的效率。

@菜鸟一枚
关注
  • 0
    点赞
  • 踩
  • 3
    收藏
    觉得还不错? 一键收藏
  • 打赏
    打赏
  • 0
    评论
C++简单排序——选择排序
小天狼星_布莱克 的博客
06-28 1万+
C++简单排序——选择排序
c++排序算法
11-24
此排序算法为本人平常学习练习所写，在学习的过程中也是非常希望和大家分享交流
c++所有排序算法的总结
07-25
有10余种排序算法的代码和图解分析,同时还有之间的区别,其中涉及到一些基础的数据结构,树,图,二叉树,堆等.堆排序,快速排序,希尔排序,归并排序,插入排序,选择....
C/C++排序算法（二） —— 选择排序和堆排序
热门推荐
Edison's 小宇宙
02-11 1万+
选择排序和堆排序算法
C++算法之选择排序
qishuiye的博客
06-24 831
C++算法之选择排序
直接选择排序算法——C/C++
有人_295的博客
06-12 1535
直接选择排序 1、算法思想 选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理：首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。 2、排序步骤 2.1、默认下标最小的为开始数据，记录下标key。 2.2、从第二个数据开始排序，进行数据比较，如果a...
基本排序算法--冒泡排序随笔
qq_39668819的博客
12-18 367
简介 冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。 它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。 这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同碳酸饮料中二氧化碳的气...
c++实现选择排序的几种方式
一曲无痕奈何
10-26 7144
一、选择排序 第一种类型： 思路：10,15,20,1,2,3,6,45,21,22 由当前位置的后一个位置，去寻找最小的然后与当前位置做一次交换即可，也就是，现在位置是0数字是10，现在向后找最小的，每次向后找，与一开始的值比较，直到拿到最小值，然后与当前的位置作一次交换，最后执行多次，直到...
选择排序实现（C++）
m0_73125687的博客
10-24 8415
排序算法之耻2号——选择排序
C++常见排序算法——选择排序算法
lengxuan001的博客
10-15 5166
首先说一下选择排序的基本算法思想： 如果有N个元素需要排序，那么首先从N个元素中找到最小的那个元素与第0位置上的元素交换，然后再从剩下的N-1个元素中找到最小的元素与第1位置上的元素交换，之后再从剩下的N-2个元素中找到最小的元素与第2位置上的元素交换，.......直到所有元素都排序好。 以从小到大排序为例：a[5]={3,5,4,1,0}; 选择出5个元素中最小的0，与a[0]，也就是3进行交换，交换后的序列变为{0,5,4,1,3}； 选择出后面4个元素中最小的1，与a[1]，也就是5进行交换
c++排序算法-冒泡排序
11-08
冒泡排序
C++ 排序算法之冒泡排序
07-25
C++ 排序算法之冒泡排序
简单的C++排序算法
11-21
一看就懂，一学就会的C++排序算法。学习数组使用，用数组下标进行选择排序，用双循环实现选择排序。 选择排序（Selection sort）是一种简单直观的排序算法。它的工作原理是：第一次从待排序的数据元素中选出最小...
C++教学——从入门到精通 10.循环
QIPABOSHI的博客
04-24 375
一些事嘛，需要重复做，这就是循环在开始学之前我提一个事，最好先学Python再学C++，不然就会像我和piaojunhe_0825一样有C++后遗症，在Python里写了一个for(int i=0;i
【C】 初识C语言
努力学习C/C++
04-21 776
从本篇开始，带你从不会C语言到精通C语言。这篇是让大家对C语言有个初步的了解。下面的内容会拆分不同篇幅单独进行详细讲叙。数据类型变量、常量字符串转义字符注释选择语句循环语句函数数组操作符常见关键字define定义常量和宏指针结构体1.什么是C语言？C语言是一门面向过程的计算机编程语言，与C++、C#、Java等面向对象编程语言有所不同。C语言的设计目标是提供一种能以简易的方式编译、处理低级存储器、仅产生少量的机器码以及不需要任何运行环境支持便能运行的编程语言。
C++ WebServer的细节理解
我的博客
04-22 626
在非阻塞模式下，如果 I/O 操作不能立即完成（例如，因为没有数据可读 或 写缓冲区满），系统不会让调用进程阻塞等待，而是立即返回一个错误（通常为 EAGAIN 或 EWOULDBLOCK）。先查询文件描述符 fd 当前的标志，然后将 O_NONBLOCK 标志加入其中，并通过 F_SETFL 来更新文件描述符，最终实现将该文件描述符切换为非阻塞模式。这意味着，如果没有待处理的连接请求（即没有客户端尝试连接到服务器），accept() 会一直阻塞，直到有新的连接请求到达或发生其他特定条件（如超时）为止。
笨蛋学C++【C++基础第六弹】
YSL_Monet的博客
04-24 830
定义类需要用到关键字 class，然后指定类的名称，类的主体是包含在一对花括号中，主体包含类的成员变量和成员函数class 类名{访问修饰符（public/protected/private）:成员变量;成员函数();
C语言如何⽤指针为函数传递数组？
最新发布
PAP
04-25 207
C语言如何⽤指针为函数传递数组？
c++排序算法及其实现
05-19
C++中有许多不同的排序算法，包括冒泡排序、选择排序、插入排序、快速排序、希尔排序、归并排序等等。以下是其中一些算法的实现示例： 1. 冒泡排序 ``` void bubbleSort(int arr[], int n) { int i, j; for (i =...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

@菜鸟一枚

你的鼓励是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值