目录
3. 57爬楼梯问题、跳跃游戏ii与零钱兑换ii的区别和联系
一、什么是递归
递归是一种函数,既然是函数那就必须符合函数的一些定义。比如:
- 递归也是一段具有特定功能的、可以重复使用的语句组。
- 递归也是用def关键开头,后面接函数名和圆括号,圆括号里面是函数的参数。
- 递归也使用return返回结果。
- 递归是一种特殊的函数,它特殊在递归函数一定会有调用自身的情况。既然是调用自身,那么必然需要明确两个问题。
问题一:递归如何调用自身?
递归调用自身一定要存在一个链条,这个链条就是上一个状态和下一个状态或者是上一项和下一项或者是大规模问题和小规模问题的之前的联系。这个链条非常重要也被称为是递归式,或者是状态转移方程。
问题二:调用自身何时停止?
一旦调用自身就会形成一个环,程序会无休止的运行下去。因此需要一个终止条件来结束递归调用自身,终止条件通常会根据求解问题的状态来确定。
递归解题的弊端
1. 时间复杂度太高。
2. 递归的深度可能超过最大递归深度(maximum recursion depth exceeded in comparison)。
尽管递归有如此弊端,我们还是不得不用递归,因为很多时候使用递归解题会更便捷,比如DFS。
这些弊端1可以使用记忆化缓存的方式解决。弊端1可以修改编译器的递归深度默认值在一定程度上得到解决,但是会导致程序性能下降并且可能伴随内存溢出等问题。
二、递归的模板
下面是基础的递归模板。实际求解的问题中递归可以有很多变化,并不是完全符合模板。但是核心思想是不会变的,即调用自身+状态转移+终止条件。比如
- 我们并不利用具体的递归函数的返回值,而是使用递归函数外部的列表在递归的过程中收集某项结果,也就是回溯、深度优先搜索。
- 递归的过程中修改某项列表的值,构建一个树形结构,也就是并查集。
def recursion(<参数>):
if <终止条件>:
return <返回值>
else:#如果终止条件不满足,那么就继续调用自身
recursion(<参数>)#根据转态转移或者链条来确定如何调用自身
return <返回值>#h这里是否需要返回值需要根据求解问题的实际情况来定
三、递归的例题
(一)斐波那契数列
(二)第 N 个泰波那契数
(三)任意累积
(四)特殊的数列
(五)Pell数列
(六)神奇的89
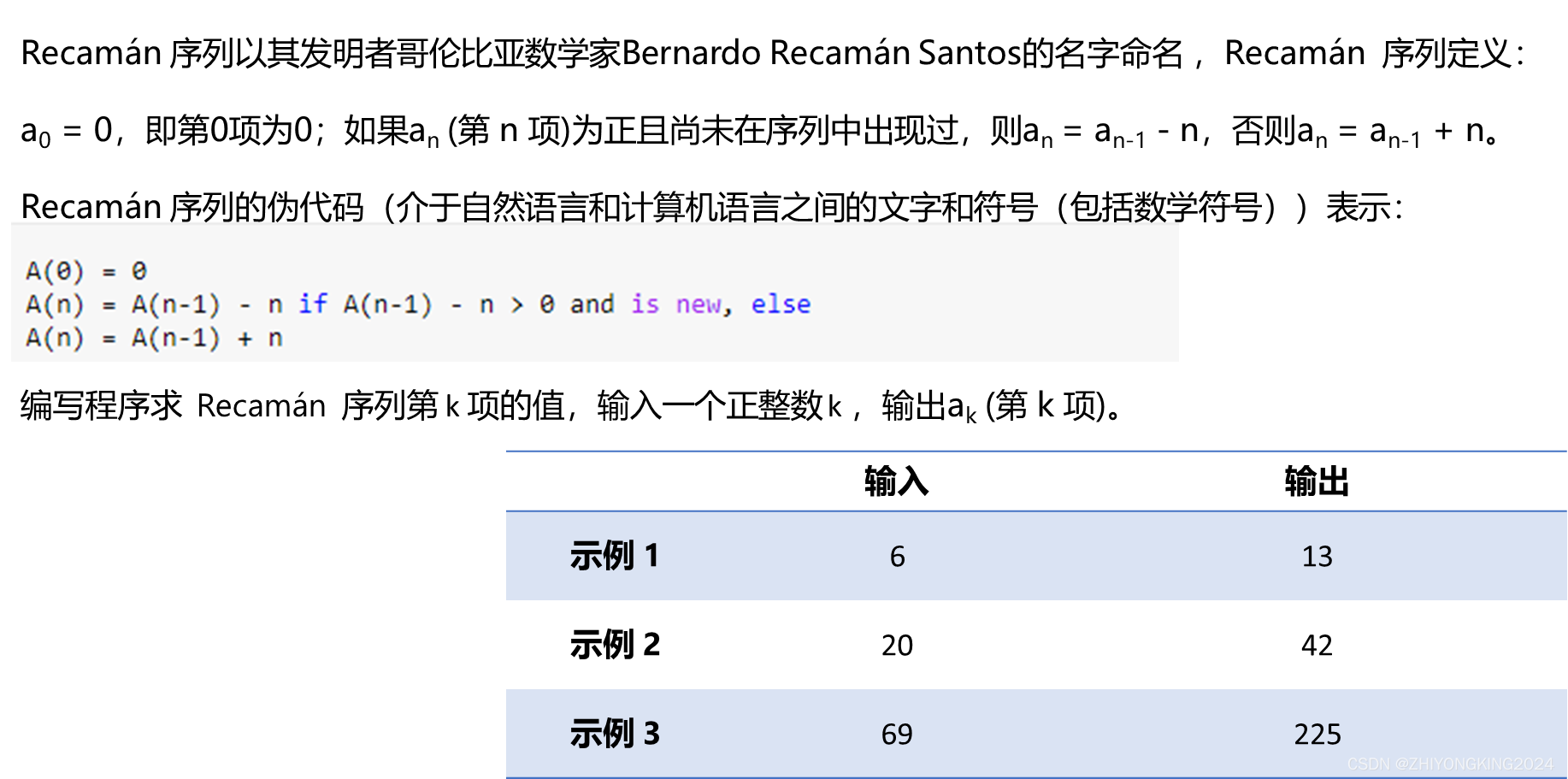
(七)Recamán 序列
(八)特殊的斐波那契数
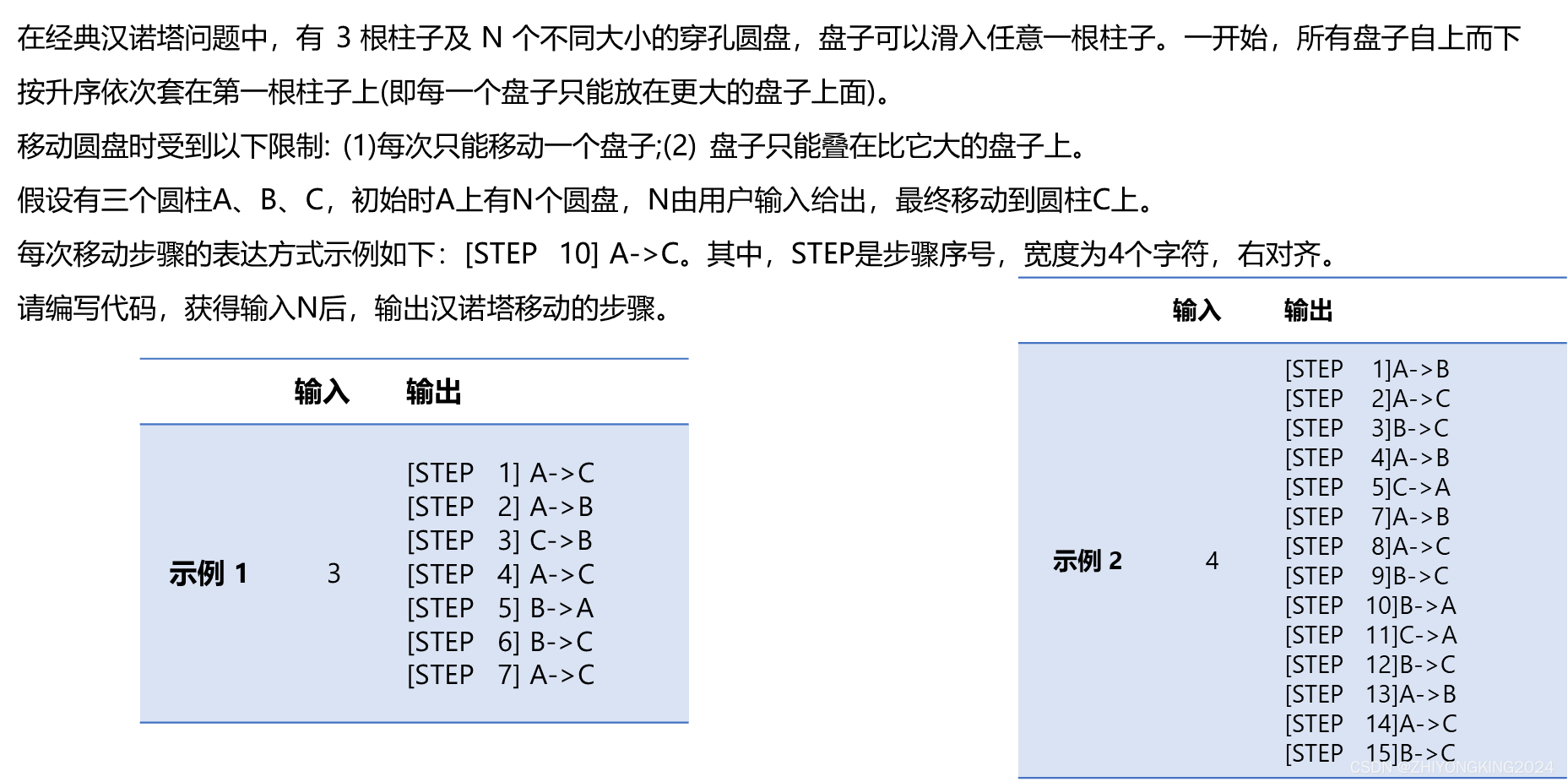
(九)汉诺塔
四、什么是动态规划
动态规划(Dynamic Programming)是一种求解问题的方法。用动态规划解决的问题最大的特征就是这些问题可以被分解为若干个重叠的子问题,这些子问题可以被重复求解,通过这些子问题的求解得出问题的解,在这些子问题的基础上求出来最终解。
常见动态规划解决的问题类型:
- 基础上问题:斐波那契数列、爬楼梯、不同路径
- 背包问题:01背包、完全背包、
- 子序列问题:最长连续子序列、最长非连续子序列
以上只是根据动规的状态转移方程的相似性进行一些简单的分类,实际上某一个问题既可以使用背包的思想去解决,也可以不适用背包思想去解决。
动态规划的基本步骤包括:
- 定义状态:确定问题的状态,也就是描述问题局部信息的变量。状态通常与问题的解相关联。
- 找出状态转移方程:定义状态之间的关系,即问题的子结构是如何组合成整体解的。这个关系通常通过递推式或者递归方程来表示。
- 初始化:确定初始状态的值。
- 计算顺序:根据状态转移方程,按照适当的顺序计算每个状态的值。
- 求解最终解:根据问题的要求,从计算得到的状态中提取最终解。
五、动态规划的模板
动态规划的核心就是将问题分解为多个小问题。这些小问题之间是有联系的,这个联系就是动态转移方程,也就是递归中的递归式或者链条。根据这个核心思想动态规划的解题可以分成几个步骤。
(一)定义状态
从题目情景中抽象出来问题是什么,这些问题该如何分解。定义状态的过程就是为了完成这件事。即确定一个dp数组,dp数组的数量代表的是将问题分解为多少个不同的子问题,dp数组的每个值代表的含义就是抽象出来到的问题,也被称为是状态。
(二)确定状态转移方程
在分解完成问题,即定义完成状态之后需要找到这些子问题之间的链条,即通过怎么进行状态的转移。当前状态怎样从其他状态那里得到。
(三)状态初始化
dp数组的初始化包含两个层面。一是整个dp数组中每个状态(小问题)的值应该初始化为什么这样不会影响才状态转移中状态的填充。二是dp数组的前面1个或者2个值的初始化,这些递归中的基例(终止条件),后面全部的状态都要从基例来的。
(四)确定遍历顺序
遍历顺序通常涉及到两个层面。一是根据状态定义和状态转移方程确定是从前往后遍历还是从后往前遍历。二是dp多维列表中,多层循环的先后嵌套安排,这一点在背包问题中体现出来。
动态规划解题步骤并不是完全单向的,比如定义完成状态之后,开始确定状态转移方程,但是发现不好确定状态转移方程,可能需要回头修改定义的状态。
六、动态规划的例题
动态规划的题目种类非常多,但是无论怎么变化还是不会脱离动态规划的核心思想。
(一)入门题目
入门题目一般是完全符合动规解题的模板的,即定义一种问题的状态、从dp[i-x]中推导出来dp[i]。
1. 斐波那契数列(LeetCode LCR 126)
斐波那契数 (通常用
F(n)表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1给定
n,请计算F(n)。答案需要取模 1e9+7(1000000007) ,如计算初始结果为:1000000008,请返回 1。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3提示:
0 <= n <= 100
2. 爬楼梯(LeetCode 70)
假设你正在爬楼梯。需要
n阶你才能到达楼顶。每次你可以爬
1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶提示:
1 <= n <= 45
3. 使用最小花费爬楼梯(LeetCode 746)
给你一个整数数组
cost,其中cost[i]是从楼梯第i个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。你可以选择从下标为
0或下标为1的台阶开始爬楼梯。请你计算并返回达到楼梯顶部的最低花费。
示例 1:
输入:cost = [10,15,20] 输出:15 解释:你将从下标为 1 的台阶开始。 - 支付 15 ,向上爬两个台阶,到达楼梯顶部。 总花费为 15 。示例 2:
输入:cost = [1,100,1,1,1,100,1,1,100,1] 输出:6 解释:你将从下标为 0 的台阶开始。 - 支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。 - 支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。 - 支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。 - 支付 1 ,向上爬一个台阶,到达楼梯顶部。 总花费为 6 。提示:
2 <= cost.length <= 10000 <= cost[i] <= 999
4.黄金分割
5. 猫吃鱼
6.金箍棒
7. 不同路径(LeetCode62)
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7 输出:28示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下示例 3:
输入:m = 7, n = 3 输出:28示例 4:
输入:m = 3, n = 3 输出:6提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
8.不同路径II(LeetCode63)
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用
1和0来表示。示例 1:
输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] 输出:2 解释:3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有2条不同的路径: 1. 向右 -> 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 -> 向右示例 2:
输入:obstacleGrid = [[0,1],[0,0]] 输出:1提示:
m == obstacleGrid.lengthn == obstacleGrid[i].length1 <= m, n <= 100obstacleGrid[i][j]为0或1
9.打家劫舍(LeetCode198)
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1] 输出:4 解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。示例 2:
输入:[2,7,9,3,1] 输出:12 解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。提示:
1 <= nums.length <= 1000 <= nums[i] <= 400
10.打家劫舍ii(LeetCode213)
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2] 输出:3 解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。示例 2:
输入:nums = [1,2,3,1] 输出:4 解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。示例 3:
输入:nums = [1,2,3] 输出:3提示:
1 <= nums.length <= 1000 <= nums[i] <= 1000
11.有毒的房间
(二)dp状态不是一个
在定义状态时需要两个或者以上子问题,每一次的状态转移都要求出来这些两个或者两个以上的状态。
需要定义两种不同的dp[i]状态,每种对应不同的情况,每一种情况都用得上。
1. 买股票的最佳时机(LeetCode121)
给定一个数组
prices,它的第i个元素prices[i]表示一支给定股票第i天的价格。你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回
0。示例 1:
输入:[7,1,5,3,6,4] 输出:5 解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。示例 2:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。提示:
1 <= prices.length <= 1050 <= prices[i] <= 104
2. 买股票的最佳时机ii(LeetCode122)
给你一个整数数组
prices,其中prices[i]表示某支股票第i天的价格。在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4] 输出:7 解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。 随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。 总利润为 4 + 3 = 7 。示例 2:
输入:prices = [1,2,3,4,5] 输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。 总利润为 4 。示例 3:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。提示:
1 <= prices.length <= 3 * 1040 <= prices[i] <= 104
3.买股票的最佳时机含冷冻期(LeetCode309)
给定一个整数数组
prices,其中第prices[i]表示第i天的股票价格 。设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: prices = [1,2,3,0,2] 输出: 3 解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]示例 2:
输入: prices = [1] 输出: 0提示:
1 <= prices.length <= 50000 <= prices[i] <= 1000
4.买股票的最佳时机含手续费(LeetCode714)
给定一个整数数组
prices,其中prices[i]表示第i天的股票价格 ;整数fee代表了交易股票的手续费用。你可以无限次地完成交易,但是你每笔交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
注意:这里的一笔交易指买入持有并卖出股票的整个过程,每笔交易你只需要为支付一次手续费。
示例 1:
输入:prices = [1, 3, 2, 8, 4, 9], fee = 2 输出:8 解释:能够达到的最大利润: 在此处买入 prices[0] = 1 在此处卖出 prices[3] = 8 在此处买入 prices[4] = 4 在此处卖出 prices[5] = 9 总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8示例 2:
输入:prices = [1,3,7,5,10,3], fee = 3 输出:6提示:
1 <= prices.length <= 5 * 1041 <= prices[i] < 5 * 1040 <= fee < 5 * 104
5. 摆动序列(LeetCode376)
需要定义两种以上的dp[i]状态,每种对应不同的情况,每一种情况都用得上。
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。- 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组
nums,返回nums中作为 摆动序列 的 最长子序列的长度 。示例 1:
输入:nums = [1,7,4,9,2,5] 输出:6 解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。示例 2:
输入:nums = [1,17,5,10,13,15,10,5,16,8] 输出:7 解释:这个序列包含几个长度为 7 摆动序列。 其中一个是 [1, 17, 10, 13, 10, 16, 8] ,各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。示例 3:
输入:nums = [1,2,3,4,5,6,7,8,9] 输出:2提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000
6.买股票的最佳时机iii(LeetCode123)
给定一个数组,它的第
i个元素是一支给定的股票在第i天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。 随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。示例 2:
输入:prices = [1,2,3,4,5] 输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。 因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。示例 3:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这个情况下, 没有交易完成, 所以最大利润为 0。示例 4:
输入:








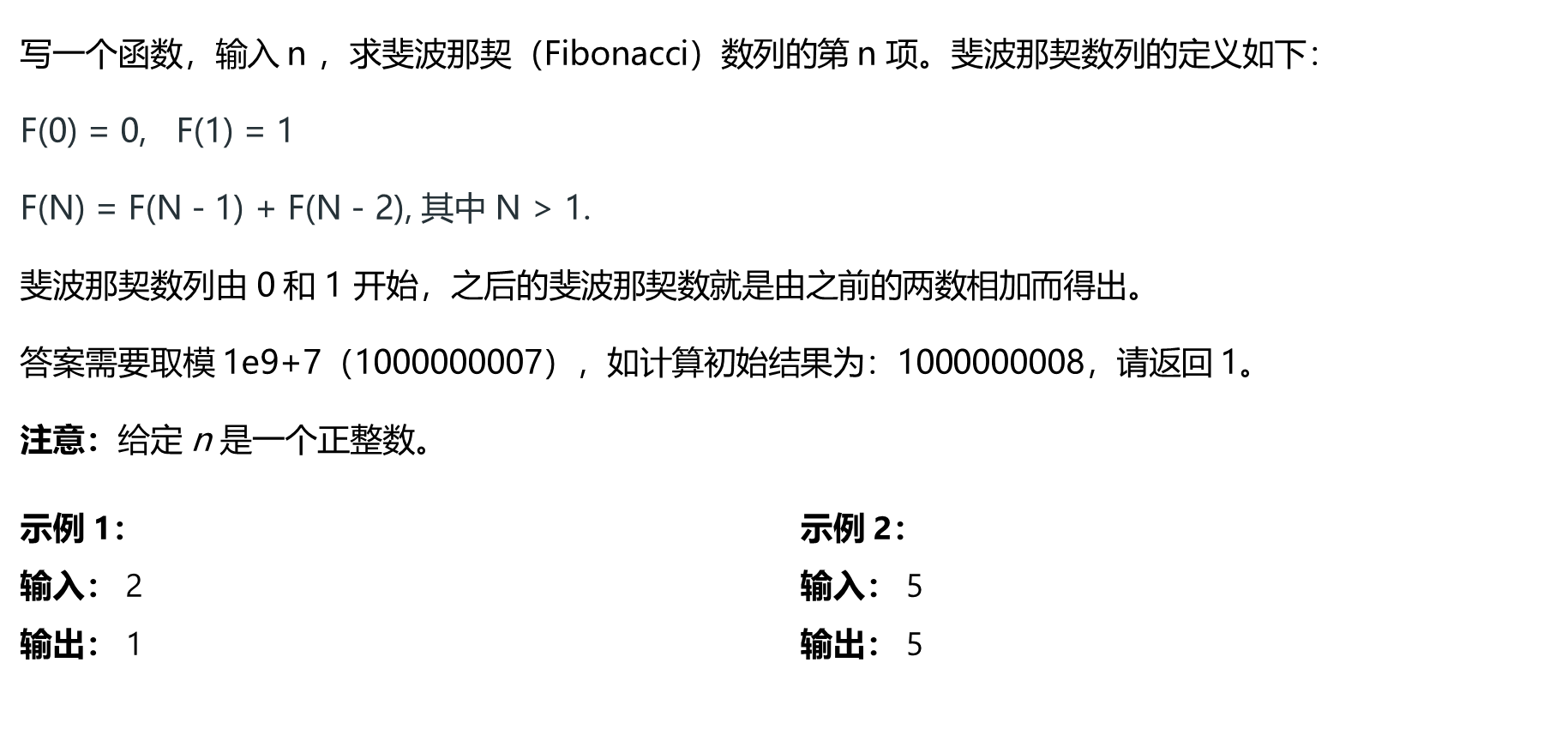













 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 1218
1218











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








