【LeetCode - 每日1题】盛最多水的容器

🌈 个人主页：（时光煮雨）
🔥 高质量专栏：vulnhub靶机渗透测试
👈 希望得到您的订阅和支持~
💡 创作高质量博文(平均质量分95+)，分享更多关于网络安全、Python领域的优质内容！（希望得到您的关注~）

---

---

难度 ⭐⭐⭐

本题要求寻找两条垂线，使其与x轴构成的容器能容纳最多的水。关键在于高效地遍历可能的容器组合，避免不必要的计算。

---

题目回顾

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

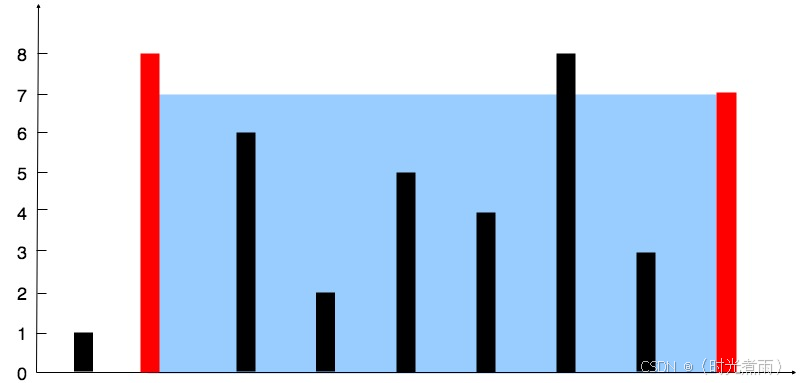
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 10**5
• 0 <= height[i] <= 10**4

---

✅解题思路​​

使用双指针策略，从数组两端开始向中间移动，每次计算当前指针位置形成的容器面积，并更新最大面积。关键在于移动高度较小的指针，因为移动较高指针无法增加容器高度，反而减少宽度。

​​💖概述​​

该问题要求在给定高度数组中找到两条垂线，使它们与x轴构成的容器能容纳最多的水。容器容量由两条垂线之间的距离（宽度）和较小高度决定。
​​

💓核心思路​​

• ​​双指针技巧​​：初始化左指针在数组起始位置，右指针在数组末尾。
• ​​面积计算​​：当前面积 = min(height[left], height[right]) * (right - left)。
• 指针移动策略​​：比较左右指针高度，移动较小高度的指针（因为移动较高指针不可能增大面积）。
• ​​贪心思想​​：通过局部最优（保留较高边）逐步逼近全局最优解。

---

✅代码实现​

from typing import List

class Solution:
    def maxArea(self, height