B. Different Divisors

最新推荐文章于 2021-09-14 18:36:59 发布

菜鸡n+1号

最新推荐文章于 2021-09-14 18:36:59 发布

阅读量260

点赞数

分类专栏： c语言数学

本文链接：https://blog.csdn.net/weixin_45410154/article/details/113732133

版权

数学同时被 2 个专栏收录

5 篇文章

订阅专栏

c语言

3 篇文章

订阅专栏

本文解析了Codeforces Round #696 (Div.2) 题目B.DifferentDivisors，介绍了如何寻找具有至少4个因子且因子间差值不小于给定整数d的最小正整数a。通过构造素数因子的方法，展示了两种不同的AC代码实现思路。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Codeforces

Round #696 (Div. 2)_B. Different Divisors

题目连接：https://codeforces.com/contest/1474/problem/B

原题

在这里插入图片描述
input

2
1
2

output

6
15

在这里插入图片描述

翻译：

正整数x被称为正整数y的除数，如果y能被x整除而无余数。例如，1是7的除数，3不是8的除数。
我们给了你一个整数d让你找出最小的正整数a，这样a至少有4个因子;
a的任意两个因数之差至少为d。
输入
第一行包含单个整数t(1≤t≤3000)-测试用例的数量。
每个测试用例的第一行包含单个整数d(1≤d≤10000)。
输出
对于每个测试用例，打印一个整数a——这个测试用例的答案。
请注意
在第一个测试用例中，整数6有以下因数:[1,2,3,6]。一共有4个，任意两个的差值至少为1。没有比这更小的整数至少有4个因数。
在第二个测试用例中，整数15有以下因数:[1,3,5,15]。一共有4个，任意两个的差值至少为2。
答案12是无效的，因为因子是[1,2,3,4,6,12]。比如，因子2和3的差小于d=2。

解题思路：

示意图：
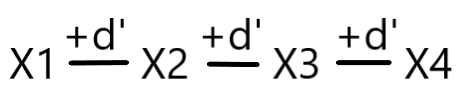
在这里插入图片描述
据题意，先给出一个整数 t，代表 t 组测试样例，每组样例给出一个整数 d，代表a的任意两个因数之差至少为d ，让我们找出最小的正整数a。
x1、x2 、x3 、x4分别为a的四个因子，d‘ 大于等于d。要使得a最小，使x1=1，x4=x2x3（x4=x2x3自然大于d），所以a=x2*x3。x为a的因子且让a的任意因子之差都不小于d，就要使x2、x3均为素数，这样才能使得这四个因子之间没有其它因子。
要注意a的值会超int。

自己的AC代码

#include<stdio.h>
#include<math.h>
typedef long long  ll;
ll sushu(ll num)
{
	bool flag;
	do
	{
		flag=true;
		for(ll i=2;i<=sqrt(num);i++)
			if(num%i==0){
				flag=false;
				break;
			}
		num++;
	}while(!flag);
	return --num;
}
int main()
{
	ll t;
	scanf("%d",&t); 
	while(t--)
	{
		ll d,ss1,ss2;
		scanf("%d",&d);
		ss1=sushu(d+1);
		ss2=sushu(ss1+d);
		printf("%lld\n",ss1*ss2);
	}


	return 0;
}

大佬的AC代码

#include<bits/stdc++.h>
#define ll long long
#define dbg(x) cout<<#x<<": "<<x<<endl;
#define N 300005
#define M 1000000007
#define pii pair<ll,ll>
#define fast ios_base::sync_with_stdio(0);cin.tie(0);
using namespace std;
bool comp[N];
vector<int>all;
void solve()
{
    int d;
    cin>>d;
    int p=*lower_bound(all.begin(),all.end(),d+1);
    int q=*lower_bound(all.begin(),all.end(),p+d);
    cout<<1LL*p*q<<'\n';
}
main()
{
    for(int i=2;i<N;i++)
    {
        if(comp[i]==0)
        {
            for(int j=i*2;j<N;j+=i)
            {
                comp[j]=1;
            }
        }
        if(comp[i]==0)
        {
            all.push_back(i);
        }
    }
 
 
    fast;
    int t;
    cin>>t;
    while(t--)
    {
        solve();
    }
}