数据结构学习之路-二叉树

树的通用概念及结构

学习二叉树之前，先了解一下树的概念。二叉树只是一种特殊结构的树。

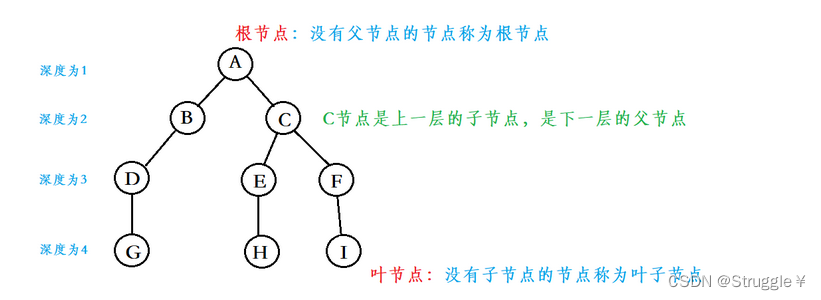
树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

• 根节点：根节点没有前驱节点。

• 叶子节点：没有后继节点的节点

• 节点的度：节点的子节点的个数，比如A节点，子节点有B和C，那么A的度就为2（对于二叉树来说，节点的度最大为2）

• 节点的深度：从根节点到当前节点的唯一路径上的节点总数，比如G节点的深度为4，E节点的深度为3，C节点的深度为2

• 节点的高度：从当前节点到最远叶子节点的路径上的节点总数，比如A节点到最远叶子节点G/H/I的路径上节点总数为4，所以A节点的高度就为4，C节点到最远叶子节点H/I的路径上节点总数为3，那么C节点的高度就为3。

• 树的高度：所有节点高度的最大值

• 树的深度：所有节点深度的最大值

二叉树的基本概念

二叉树最明显的特点就是：每个节点的度最大为2（最多拥有两棵子树）

二叉树还有一个重要的特点就是：左子树和右子树数有明确定义的，左就是左，右就是右。即使某个节点只有一课子树，也要区分左右子树。

下面介绍几种特殊的二叉树：

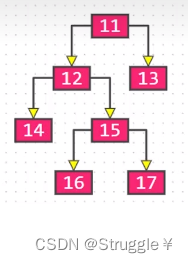
• 真二叉树：所有节点的度，要么为0，要么为2，没有度为1的节点。比如下图这种
  

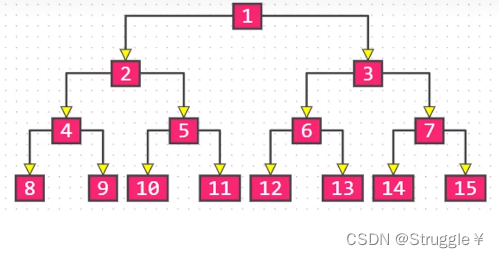
• 满二叉树：所有节点的度，要么为0，要么为2。且所有的叶子节点都在最后一层。想要满足这些条件，这个二叉树就是满的，即所有的位置都有节点，如下图所示：
  

• 完全二叉树：叶子节点只会出现在最后两层，且最后一层的叶子节点都靠左对齐
  
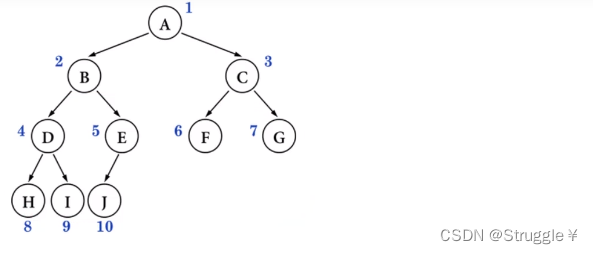
  假如，J节点是E节点的右子节点，那么这棵树就不是完全二叉树。如果E节点没满，恰好F或者G有节点，那这棵树也不是完全二叉树。因为都没满足靠左对齐的条件。（完全二叉树从根节点到倒数第二层是一棵满二叉树）

这里多说一点完全二叉树的性质，因为完全二叉树挺重要的：

• 度为1的节点，只可能是左子树（这就是叶子节点靠左对齐的性质）

• 度为1的节点，要么是一个，要么是0个

• 相同节点总数的二叉树，完全二叉树的高度是最小的

• 一个拥有n个节点的完全二叉树（n>0），从上到下从左到右对节点从0开始进行编号，那么任意第i个节点都有如下性质：
  1、如果i = 0，该节点是根节点
  2、如果i > 0，该节点的父节点编号为floor((i-1)/2)
  3、如果2i + 1<= n -1，该节点一定要左子节点，且编号为2i+1
  4、如果2i + 1> n，该节点一定无左子节点
  5、如果2i + 2 <= n - 1，该节点一定有右子节点，且编号为2i + 2
  

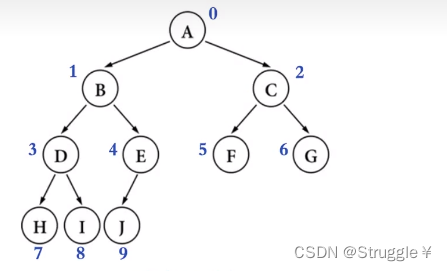
来一道面试题：如果一棵完全二叉树有768个节点，求叶子节点的个数。（最后可总结出万能公式）

1、假设叶子节点个数为n0，度为1的节点个数为n1，度为2的节点个数为n2
那么总节点个数为n = n0 + n1 + n2，
2、完全二叉树有一个公式就是叶子节点的个数为度为2节点个数加1，即n0 = n2 + 1

3、结合两个公式得出：n = 2n0 + n1 - 1
4、完全二叉树，度为1的节点个数要么是1个，要么是0个

综合上述条件我们开始解题：

• 如果度为1的节点只有1个，那么n1 = 1，n = 2n0，也就是说n必须是偶数，所以n0 = n / 2
• 如果度为1的节点只有0个，那么n1 = 0，n = 2n0 - 1，也就是说n必须是奇数，所以n0 = (n + 1) / 2

本题节点总数是768，是偶数，也就是符合第一个条件，所以n0 = n / 2 = 768 / 2 = 394。

有没有一个办法不判断总节点数是奇数还是偶数，就能把叶子节点的个数求出来呢？当然是直接n0 = floor((n + 1) / 2)向下取整，如果n是奇数，不影响，如果n是偶数，向下取整，就会忽略 +1，实在是一个完美的公式。

二叉搜索树（BinarySearchTree）

二叉搜索树是非常重要的一种二叉树，为什么要引入二叉搜索树呢？下面我们来思考一个问题：

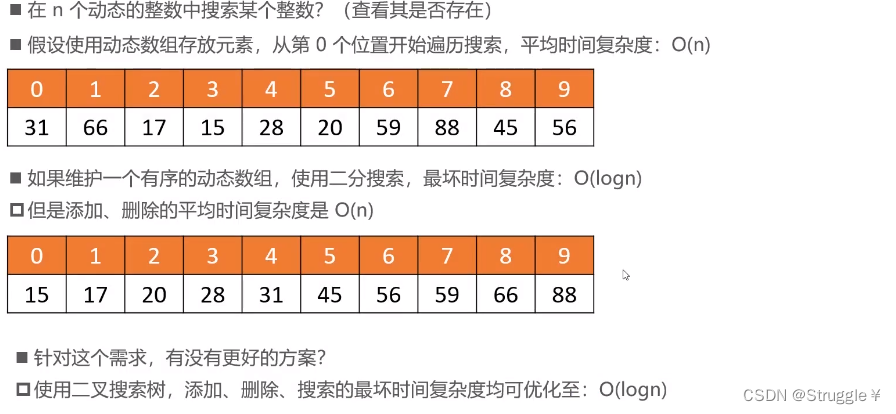
二叉搜索树的特点

• 任意一个节点的值都大于其左子树所有节点的值
• 任意一个节点的值都小于其右子树所有节点的值
• 它的左右子树也是一棵二叉搜索树
• 二叉搜索树的元素必须具备可比较性（比如int double，如果是自定义类型，需要指定比较方式，不允许节点为null）

二叉搜索树的接口设计

需要注意的是，二叉搜索树是没有索引的概念的，所以也没有根据index获取元素的接口。

二叉搜索树上每一个节点需要一个节点类来维护，我们这么设计二叉搜索树的节点：

private static class Node<Type>{
    Type element; //节点内部存储的值
    Node<Type> leftChildNode; //该节点的左子节点
    Node<Type> rightChildNode; //该节点的右子节点
    Node<Type> parentNode; //该节点的父节点

    public Node(Type element, Node<Type> parentNode) {
        this.element = element;
        this.parentNode = parentNode;
    }
}

说明：每一个节点的内部有四个成员变量，详情见注释。构造函数为什么只传两个参数呢？因为创建一个新的节点，除了根节点都有父节点，而且都得有值。相反，创建一个节点，左右子节点不一定存在，因此不需要作为构造函数的入口参数。

二叉搜索树支持泛型，且有两个成员变量，一个是记录树中节点的个数size，一个是记录树的根节点rootNode（因为搜索任意一个节点，都要从根节点出发）

public class BinarySearchTree<Type> {
    private int size;
    private Node<Type> rootNode;
}

下面我们就开始二叉搜索树每一个接口的设计：

向二叉搜索树中添加节点

• 添加节点：void add(Type element)

功能就是：入口参数传入Type类型的元素element，会根据二叉搜索树的规则插入到合理的位置。最重要的就是这个二叉搜索树的规则：任意节点的值都小于右子节点且都大于左子节点。因此，在插入任意一个新的节点的时候，都要比大小。换句话说，能成为二叉搜索树中节点的必要条件是节点具有可比较性！！！

现在细说设计思路：

1、二叉搜索树要求节点的元素值不能为null，因此写一个接口来判断

public void elementNotNullCheck(Type element){
    if(element == null){
        throw new IllegalArgumentException("element must not be null");
    }
}

2、当添加的节点是根节点时，也就是搜索树在此之前是空的，此时只需要对根节点进行创建即可。因为根节点没有父节点，因此第二个参数传null即可，size++，然后直接返回即可。

public void add(Type element){
    elementNotNullCheck(element);//判断添加的节点的元素值是否为null

    //如果添加的是根节点，意味着此时二叉树是空的
    if(rootNode == null){
        rootNode = new Node<>(element,null);//根节点的父节点就是null，因为没有父节点
        size++;
        return;
    }

	//......   
}

当下次add节点时，根节点就不为空了，这段代码也就不执行了。

3、添加的节点不是根节点时，那就得通过比大小来进行插入了。具体的插入过程需要遵守三步准则：

• 找到插入的位置（包括找到插入处的父节点是哪个节点，插到父节点的左边还是右边）
• 创建该节点（依靠传入的element和找到的父节点）
• 根据插入位置，赋值到父节点的左子节点或者右子节点

几个关键点：需要通过循环来找到插入的位置，循环结束的条件就是找到的节点为null（因为节点为空说明不具备左右子节点属性，紧接着循环结束前的那个节点就是我们要找到的父节点）；父节点和方向需要写在循环外面，保证循环结束可以拿到；在找到父节点和确定方向之后，紧接着就利用传进来的element创建新节点，然后根据方向结果赋值给父节点的左子节点或者右子节点即可；插入节点别忘了size++。

public void add(Type element){
    elementNotNullCheck(element);//判断添加的节点的元素值是否为null

    //如果添加的是根节点，意味着此时二叉树是空的
    if(rootNode == null){
        rootNode = new Node<>(element,null);//根节点的父节点就是null，因为没有父节点
        size++;
        return;
    }

    //程序能到这，说明二叉树已经存在根节点了，那我们添加的就是普通节点了
    /**
     * 添加节点的步骤：
     * 1、找到该节点的插入位置，也就是找到父节点（这一步是核心步骤）
     * 2、创建该节点
     * 3、判断比父节点大还是比父节点小，从而判断是左子节点还是右子节点
     * 如果遇到值相等的元素，那就覆盖掉原有节点
     */

    //任何节点都是从父节点开始找的，所以首先赋值父节点
    Node<Type> currentNode = rootNode;
    //循环的目的是找到插入节点的父节点，因此需要在循环结束的前一刻拿到父节点，初始默认根节点就是父节点
    Node<Type> parent = rootNode;
    //循环的目的不仅要找到插入节点的父节点，还要知道插在左边还是插在右边，因此方向也要记录,所以把决定方向的变量放在循环外面
    int cmp_result = 0;

    while (currentNode != null){
        //当前节点不为空，才可以继续比较；如果在不断地比较之后，当前节点currentNode等于null，说明不能继续比了，此时就要把传进来的节点插入了
        cmp_result = compareNode(element, currentNode.element);
        parent = currentNode;
        if(cmp_result > 0){
            //说明传进来的element大于当前节点的element，那就得向右子树进行搜索，然后继续比较
            currentNode = currentNode.rightChildNode;

        } else if(cmp_result < 0){
            //说明传进来的element小于当前节点的element，那就得向左子树进行搜索，然后继续比较
            currentNode = currentNode.leftChildNode;

        }else {
            // 说明当前节点的element和传进来的element相等，那就覆盖当前值
            currentNode.element = element;
            return;
        }
    }

    //循环完毕，currentNode一定为空，所以要提前保存插入节点的父节点，还要提取保存插入方向
    //创建该节点，把传进来的element赋值给该节点，因为循环结束就知道父节点是谁了，因此这里直接传入
    Node<Type> newNode = new Node<>(element,parent);
    //判断比父节点大还是比父节点小，从而判断是左子节点还是右子节点
    if(cmp_result > 0){
        //说明该插向右边
        parent.rightChildNode = newNode;
    }else {
        //说明该插向左边
        parent.leftChildNode = newNode;
    }

    size++;//插入完毕后，size要+1

}

既然要求节点之间是可比较的，我们在add函数中通过compareNode(element, currentNode.element)函数来比较插入元素和二叉搜索树中其他元素的大小。如果element是int类型，直接比大小就ok了。但是，我们是支持泛型的，万一将来传入的是自定义类型，怎么比较呢？

这里用到的是java中的条件泛型，首先我们声明一个接口，叫做Comparable，意思是可比较性的接口，里面有一个接口函数，表示比较函数。

package com.xhb;

public interface Comparable<Type> {
    int compareTo(Type e);
}

比如，我们想要在二叉搜索树中插入Person类型的数据，并根据其成员变量age进行比大小，age大的，认为Person对象就大。Person类需要实现我们自定义的Comparable接口，并声明泛型类型。通过实现compareTo函数，可以判断两个Person对象的大小。返回值0表示当前对象等于待比较对象,大于0表示当前对象大于待比较对象，小于0表示当前对象小于待比较对象。

package com.xhb;

public class Person implements Comparable<Person> {
    int age;

    public Person(int age) {
        this.age = age;
    }

    @Override
    public int compareTo(Person e) {
        return age - e.age;
    }
}

最最最关键的一步来了，二叉搜索树类的泛型Type要继承接口Comparable，表示Type类型的数据必须实现Comparable里的接口，也就是上面的Person类实现Comparable的接口函数。这也就是意味着，将来插入的Type类型必须是可比较的，无论是什么比较方式。

package com.xhb;

public class BinarySearchTree<Type extends Comparable> {
    private int size;
    private Node<Type> rootNode;
}

都完成之后，我们在二叉搜索树类里实现比较两个节点大小的函数compareNode，这样就可以比较e1和e2的大小。

/**
 * 比较两个元素值的大小，从此判断是放在左子树还是右子树。比较的元素不一定是int，还可能是Person类型，因此这里的比较规则必须做到复用
 * @param e1
 * @param e2
 * @return 0表示e1等于e2,大于0表示e1大于e2，小于0表示e1小于e2
 */
public int compareNode(Type e1, Type e2){
   return e1.compareTo(e2);
}

我们在main函数测试一下：插入不报错，说明插入成功。

package com.xhb;

public class Main {

    public static void main(String[] args) {

        BinarySearchTree<Person> bst = new BinarySearchTree<>();
        bst.add(new Person(10));
        bst.add(new Person(17));
        bst.add(new Person(9));
    }
}

但是，这种设计我认为是有问题的！

假如，我想要声明两个不同的二叉搜索树，都以Person类型的数据作为节点元素。但是两个二叉搜索树的比较规则不一样。第一个二叉搜索树认为年龄age大的Person对象大，第二个认为年龄age小的Person对象大。如果按照上面的设计方式，下面的bst1和bst2在插入新元素时，都遵循相同的比较规则，我觉得这是不灵活的。

public static void main(String[] args) {

    BinarySearchTree<Person> bst1 = new BinarySearchTree<>();
    bst1.add(new Person(10));
    bst1.add(new Person(17));
    bst1.add(new Person(9));

    BinarySearchTree<Person> bst2 = new BinarySearchTree<>();
    bst2.add(new Person(9));
    bst2.add(new Person(10));
    bst2.add(new Person(17));
}

因此，我们需要重新设计比较器。这里我们再声明一个比较器接口Comparator，内部有一个接口函数compare，用来比较两个Type类型的数据大小。

package com.xhb;

public interface Comparator<Type> {
    int compare(Type e1, Type e2);
}

然后在二叉搜索树类内声明BinarySearchTree的构造函数，并定义一个比较器的成员变量。构造函数的入口参数就是比较器对象，然后把外部传入的比较器对象赋值给BinarySearchTree类内的比较器对象

public class BinarySearchTree<Type> {
    private int size;
    private Node<Type> rootNode;
    
    private Comparator<Type> comparator;
    /**
     * 构造函数支持传入比较器对象
     * @param comparator
     */
    public BinarySearchTree(Comparator<Type> comparator) {
        this.comparator = comparator;
    }
}

然后，利用比较器对象，调用接口函数，完成比较：

public int compareNode(Type e1, Type e2){
   return comparator.compare(e1,e2);
}

至于这个接口函数是怎么实现的，只需要在外部灵活实现即可。定义一个新的比较器类，然后实现Comparator里的接口函数compare，至于内部怎么实现，自己定义即可。然后在声明BinarySearchTree对象时，就把该类的对象传入到构造函数，完成比较器的嵌入。

public class Main {

    private static class BigAgePersonComparator implements Comparator<Person>{
        @Override
        public int compare(Person e1, Person e2) {
            return e1.age - e2.age;
        }
    }

    private static class SmallAgePersonComparator implements Comparator<Person>{
        @Override
        public int compare(Person e1, Person e2) {
            return e2.age - e1.age;
        }
    }

    public static void main(String[] args) {

        BinarySearchTree<Person> bst = new BinarySearchTree<>(new BigAgePersonComparator());
        bst.add(new Person(10));
        bst.add(new Person(17));
        bst.add(new Person(9));

        BinarySearchTree<Person> bst2 = new BinarySearchTree<>(new SmallAgePersonComparator());
        bst2.add(new Person(9));
        bst2.add(new Person(10));
        bst2.add(new Person(17));

    }
}

通过上面的代码也可以看出，只需要传入不同的参数到构造函数，就能实现不同的比较规则，进而创建不同比较规则的二叉搜索树，这才是灵活的二叉搜索树设计范式。但不是最灵活的，因为这种需求只是可能存在，并不一定存在。假设，我们在创建二叉搜索树的时候，就不想指定不同的比较逻辑。也就意味着，有时候我们并不想强制传入一个比较器给构造函数。所以，最最最灵活的设计方式是重载构造函数，可以实现想传就传，想不传就不传。

声明两个重载的构造函数，一个需要传自定义的比较器，一个不需要传比较器（将比较器置位null）

public class BinarySearchTree<Type> {
    private int size;
    private Node<Type> rootNode;
    private Comparator<Type> comparator;

    public BinarySearchTree() {
        this(null);
    }

    /**
     * 构造函数支持传入比较器对象
     * @param comparator
     */
    public BinarySearchTree(Comparator<Type> comparator) {
        this.comparator = comparator;
    }
}

紧接着，BinarySearchTree类内的比较节点函数compareNode就要这样实现：首先判断比较器是否为null，这一步也就是判断是否传入了自定义的比较器，如果不为空，那就调用比较器的比较函数comparator.compare(e1,e2);如果为空，那就调用Type类型类内部自定义的可比较函数。

public int compareNode(Type e1, Type e2){
    if(comparator != null){
        return comparator.compare(e1,e2);
    }
    return ((Comparable<Type>)e1).compareTo(e2);
}

完成上述设计，可以实现什么样的效果呢？

可以实现：不传自定义比较器的Person，按照Person类内实现的可比较函数的规则来创建二叉搜索树。传入自定义比较器的Person类，按照比较器实现的比较函数来创建二叉搜索树。非常灵活！！！

public class Main {

    private static class SmallAgePersonComparator implements Comparator<Person>{
        @Override
        public int compare(Person e1, Person e2) {
            return e2.age - e1.age;
        }
    }

    public static void main(String[] args) {

        BinarySearchTree<Person> bst = new BinarySearchTree<>();
        bst.add(new Person(10));
        bst.add(new Person(17));
        bst.add(new Person(9));

        BinarySearchTree<Person> bst2 = new BinarySearchTree<>(new SmallAgePersonComparator());
        bst2.add(new Person(9));
        bst2.add(new Person(10));
        bst2.add(new Person(17));
    }
}

public class Person implements Comparable<Person> {
    int age;

    public Person(int age) {
        this.age = age;
    }

    @Override
    public int compareTo(Person e) {
        return age - e.age;
    }
}

这还是不最最最牛逼的，最牛逼的是，我们创建一个存放int类型元素的二叉搜索树时，我们这么设计，仍然是可用的。因为int内部官方已经实现了比较器，所以，我们就可以不传任何自定义的比较器，也可以通用我们设计的二叉搜索树类。

可比较和比较器，都已经被实现了，因此，我们在设计二叉搜索树类时，直接导入即可。

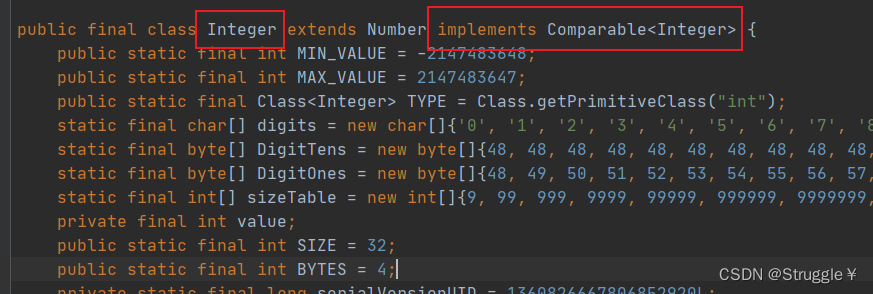
因此，自定义类型，比如Person类直接导入可比较接口Comparable即可

package com.xhb;
import java.lang.Comparable;

public class Person implements Comparable<Person> {
    int age;

    public Person(int age) {
        this.age = age;
    }

    @Override
    public int compareTo(Person e) {
        return age - e.age;
    }
}

二叉搜索树类，直接导入比较器Comparator即可

import java.util.Comparator;

public class BinarySearchTree<Type> {
    private int size;
    private Node<Type> rootNode;
    private Comparator<Type> comparator;

    public BinarySearchTree() {
        this(null);
    }

    /**
     * 构造函数支持传入比较器对象
     * @param comparator
     */
    public BinarySearchTree(Comparator<Type> comparator) {
        this.comparator = comparator;
    }
}

因此，main函数就可以这样了：想创建存放什么元素的二叉树都可以，想传比较器就传比较器，不想传即不传。对于默认有比较器的基本数据类型Integer，默认是不传比较器的。这样的一个二叉搜索树类，可以达到复用多种场景的效果，非常的niubility。

public class Main {

    private static class SmallAgePersonComparator implements Comparator<Person> {
        @Override
        public int compare(Person e1, Person e2) {
            return e2.age - e1.age;
        }
    }

    public static void main(String[] args) {

        BinarySearchTree<Person> bst = new BinarySearchTree<>();
        bst.add(new Person(10));
        bst.add(new Person(17));
        bst.add(new Person(9));

        BinarySearchTree<Person> bst2 = new BinarySearchTree<>(new SmallAgePersonComparator());
        bst2.add(new Person(9));
        bst2.add(new Person(10));
        bst2.add(new Person(17));

        BinarySearchTree<Integer> bst3 = new BinarySearchTree<>();
        bst3.add(10);
        bst3.add(17);
        bst3.add(9);

    }
}

删除二叉搜索树中的元素

• 删除叶子节点

核心思想就是让叶子节点的父节点指向null就能做到删除叶子节点的效果。

• 删除度为1的节点

核心思想就是让该节点的父节点直接指向该节点的唯一子节点，就能把这个节点删除。

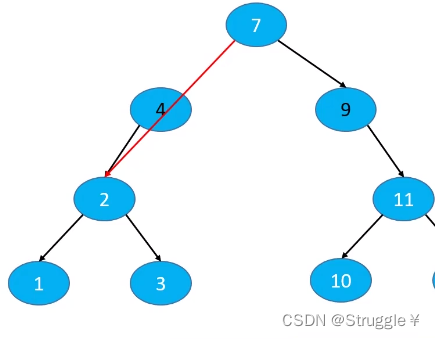
当然还是要考虑该节点是根节点的情况，直接让root指向该节点的唯一子节点即可

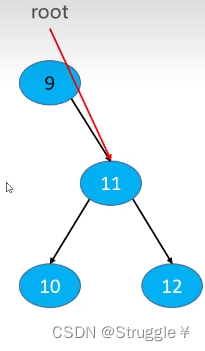
（可以看到，只要是删除节点，都要考虑这个节点是不是根节点，因为根节点的处理方式是特殊的）

• 删除度为2的节点

这是最难的一个，因为度为2的节点一旦删除，就要“安抚”好其两个子节点。

删除度为2节点的核心思想就是，从其左子树中或者右子树中，找一个合适的节点替代当前节点。这个合适的节点，就是前驱节点或者后继节点。

因为这只有这样做，才能保证该节点的左子树都是比该节点小，右子树都是比该节点大。

比如下面的例子：想要删除5，那就找到5的前驱节点4或者后继节点6，然后覆盖5的位置。覆盖完之后，删除前驱节点或者后继节点。比如删除前驱节点4，因为是叶子节点，直接删除就行；或者删除后继节点6，因为是度为1的节点，所以需要一些策略。

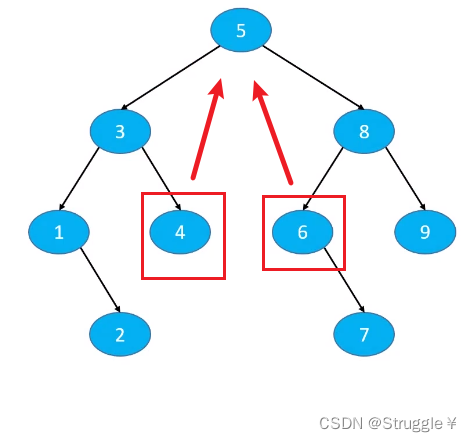
比如，用前驱节点覆盖，就是下图的样子：

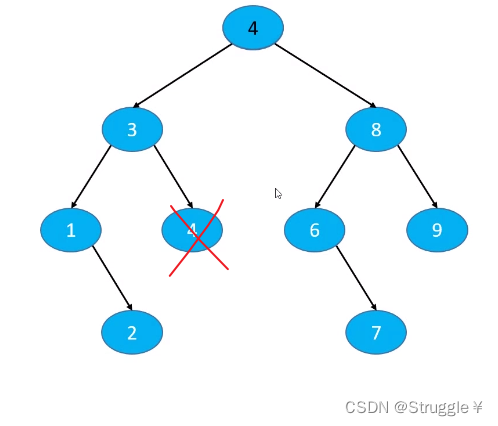
下面实现这一功能：

我们在外部调用remove函数时，传的指定是元素值。根据我们上面的分析，我们在内部实现的时候，操作的其实是节点本身。因此，我们需要封装一个函数，可以根据元素值返回节点本身。

/**
 * 传入元素值element，返回对应的节点对象
 * @param element
 * @return
 */
private Node<Type> node(Type element){
    //肯定是从根节点一路往下找
    Node<Type> node = rootNode;

    while (node != null){
        //传进来的element和某一个节点node的element进行比较
        int cmp = compareNode(element,node.element);
        if(cmp == 0) return node;//找到了
        if(cmp>0){
            //说明传入的节点要大于当前node的节点，说明想要查找的节点指定是在该节点node的右子树中，需要向右子树继续查找
            node = node.rightChildNode;
        }else{
            //否则向左子树继续查找
            node = node.leftChildNode;
        }
    }
    //如果程序执行到这，说明没有找到，那就返回null
    return null;
}

• 如果是度为0的节点，直接让父节点的左或者右子节点指向null就行了。如果这个节点是根节点，说明该树只有一个节点，直接根节点指向null

if(node.leftChildNode==null && node.rightChildNode==null){
     //如果是叶子节点
     if(node.parentNode != null){
         //说明不是根节点,直接删除
         if(node == node.parentNode.leftChildNode){
             //如果是左子节点，就删除左子节点
             node.parentNode.leftChildNode = null;
         }else {
             //如果是右子节点，就删除右子节点
             node.parentNode.rightChildNode = null;
         }
     }else {
         //说明是根节点
         rootNode = null;
     }
 }

• 如果删除的节点是度为1的，直接让node的父节点指向node的子节点，就能把node删除。如果node是根节点，那就让其子节点当新的根节点，这样node也能删除。

else if ((node.leftChildNode!=null && node.rightChildNode==null) || (node.leftChildNode==null && node.rightChildNode!=null)){
    //如果是度为1的节点
    if(node.parentNode != null){
        //说明不是根节点,那就父节点指向子节点，就可以把本身删掉
        node.parentNode = node.leftChildNode!=null ? node.leftChildNode : node.rightChildNode;
    }else {
        rootNode = node.leftChildNode!=null ? node.leftChildNode : node.rightChildNode;
    }
}

• 如果删除的节点度为2，首先需要找到前驱节点替代node，然后把前驱节点删掉即可。（因为前驱节点一定是度为1或者0，采用上面的方法即可）

else {
    //如果是度为2的节点

    //先找到前驱节点
    Node<Type> preNode = predecessor(node);
    //用前驱节点的值覆盖当前度为2的节点的值
    node.element = preNode.element;

    //然后删除前驱节点（前驱节点一定是度为1或者度为0的节点，因为度为2的节点，其左子节点一定是优先前驱）
    if(preNode.leftChildNode==null && preNode.rightChildNode==null){
        //度为0，叶子节点
        if(preNode == preNode.parentNode.rightChildNode){
            preNode.parentNode.rightChildNode = null;
        }else {
            preNode.parentNode.leftChildNode = null;
        }

    }
    if((preNode.leftChildNode!=null && preNode.rightChildNode==null) || (preNode.leftChildNode==null && preNode.rightChildNode!=null)){
        //度为1，可能是只有左子节点，也可能只有右子节点
        preNode.parentNode = preNode.leftChildNode!=null ? preNode.leftChildNode : preNode.rightChildNode;
    }

}

下面我们来测试一下：在main函数中，声明一个二叉搜索树，然后层序遍历打印，然后删除2，然后再打印

public static void main(String[] args) {

    Integer data[] = new Integer[]{7, 4, 9, 2, 5, 8, 11, 3,10, 12, 1};

    BinarySearchTree<Integer> bst = new BinarySearchTree<>();
    for (int i = 0; i < data.length ; i++) {
        bst.add(data[i]);
    }

    bst.LevelOrderTraversal(new BinarySearchTree.Visitor<Integer>() {
        @Override
        public void visit(Integer element) {
            //这里面写visit的访问逻辑
            System.out.print("_" + element);
        }
    });

    bst.remove(2);
    System.out.println("\n");

    bst.LevelOrderTraversal(new BinarySearchTree.Visitor<Integer>() {
        @Override
        public void visit(Integer element) {
            //这里面写visit的访问逻辑
            System.out.print("_" + element);
        }
    });

}

可以看到，2被删除了。其他的情况，我也均做了测试，都可以正确删除。

二叉树的遍历

遍历是数据结构中的常见操作，目的是把数据结构中的所有元素都访问一遍。

常见的线性数据结构的遍历比较简单，比如vector。遍历方式有正序遍历和逆序遍历两种。

但是二叉树没有索引的概念，因此无法像以往的数据结构一样遍历。二叉树是根据节点的访问顺序不同，其遍历方式有四种：

1. 前序遍历（Preorder Traversal）
2. 中序遍历（InorderTraversal）
3. 后序遍历（PostorderTraversal）
4. 层序遍历（Level OrderTraversal）

注意：遍历操作是二叉树都有的，并不是只有二叉搜索树才有遍历的功能。

下面介绍这几种遍历的原理，以及代码实现

前序遍历

前中后序，中的“前”“中”“后”指的是访问根节点的位置。

所以前序遍历的访问顺序是：先访问根节点，然后前序遍历左子树，最后前序遍历右子树。

注意哦，左子树和右子树也要遵循前序遍历的原则。

很容易想到递归求解，传入的参数是根节点，这里我们访问形式选择的是打印，然后依次前序遍历左子树（传入的参数顺理成章的就是左子节点），最后前序遍历右子树（传入的参数就是右子节点）

public void preOrderTraversal(){
    preOrderTraversal(rootNode);
}

/**
 * @param node 表示传入的根节点
 */
private void preOrderTraversal(Node<Type> node){
    if(node == null) return;//递归的结束条件就是node为null

    System.out.println(node.element);//这里仅仅打印出每一个访问的节点的element
    preOrderTraversal(node.leftChildNode);
    preOrderTraversal(node.rightChildNode);
}

分成两个函数来写，是体现出封装的思想。外界直接访问无参的函数即可。

这里给出一个例子，

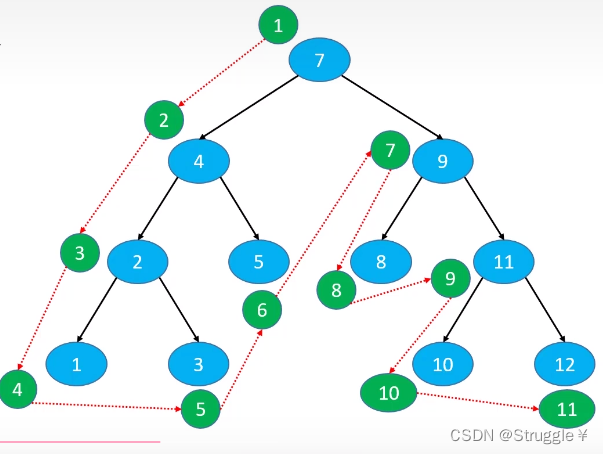
我们创建这样的一个二叉树，然后前序遍历，并依次打印出来。

public static void main(String[] args) {

   Integer data[] = new Integer[]{7, 4, 9, 2, 5, 8, 11, 3,10, 12, 1};


   BinarySearchTree<Integer> bst = new BinarySearchTree<>();
   for (int i = 0; i < data.length ; i++) {
       bst.add(data[i]);
   }

   bst.preOrderTraversal();

}

可以看出程序执行没有问题，我们成功地前序遍历了二叉树。

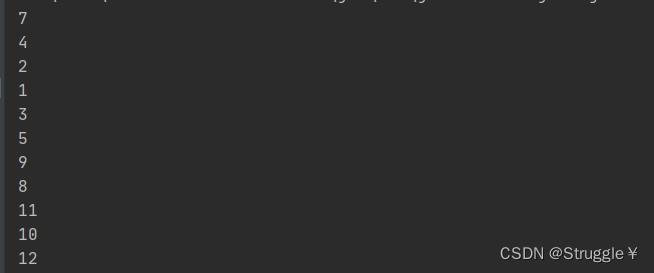
中序遍历

中序遍历即中间访问根节点，至于先中序访问左子树还是中序访问右子树，无所谓。

因此，中序遍历的访问顺序是：先中序遍历左子树，然后访问根节点，最后中序遍历右子树。

因此，递归实现如下：

public void InorderTraversal(){
   InorderTraversal(rootNode);
}

private void InorderTraversal(Node<Type> node){
   if(node == null) return;

   InorderTraversal(node.leftChildNode);
   System.out.println(node.element);
   InorderTraversal(node.rightChildNode);
}

依然使用前面的例子

public static void main(String[] args) {

    Integer data[] = new Integer[]{7, 4, 9, 2, 5, 8, 11, 3,10, 12, 1};


    BinarySearchTree<Integer> bst = new BinarySearchTree<>();
    for (int i = 0; i < data.length ; i++) {
        bst.add(data[i]);
    }

    bst.InorderTraversal();

}

程序打印结果，可以发现一个规律 ，对于二叉搜索树来说，中序遍历的结果，是按照顺序排列的。这是因为二叉搜索树就是根据元素值大小区分左子数，根节点，右子树的。

后序遍历

后序遍历，顾名思义是要最后访问根节点。

因此，访问顺序可以是：先后序遍历左子树，然后后序遍历右子树，最后访问根节点。

public void PostOrderTraversal(){
    PostOrderTraversal(rootNode);
}

private void PostOrderTraversal(Node<Type> node){
    if(node == null) return;

    PostOrderTraversal(node.leftChildNode);
    PostOrderTraversal(node.rightChildNode);
    System.out.println(node.element);
}

public static void main(String[] args) {

    Integer data[] = new Integer[]{7, 4, 9, 2, 5, 8, 11, 3,10, 12, 1};


    BinarySearchTree<Integer> bst = new BinarySearchTree<>();
    for (int i = 0; i < data.length ; i++) {
        bst.add(data[i]);
    }

    bst.PostOrderTraversal();

}

可以看出，没有问题

层序遍历

最值得学习的一个遍历方式。顾名思义，从上到下，从左到右依次访问每一个节点。

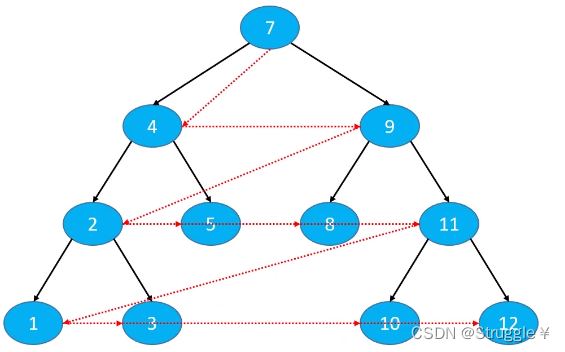
观察到一个现象：第i层先访问的节点，第i+1层相应的子节点所在层也是先被访问。因此，父节点和子节点的访问顺序，有一种先被访问父节点，就会先被访问子节点。先…先…的思想，因此这里选择使用队列来实现层序遍历。

实现思路：

1. 先将根节点入队；
2. 循环执行以下操作，直到队列为空
   2.1、将队列此时的头结点Head出队，然后进行访问
   2.2、将头结点的左子节点入队（没有就不入队）
   2.3、将头结点的右子节点入队（没有就不入队）

核心的思想就是，访问并出队某个父节点的那一刻，立马把其子节点入队。虽然队列里还有与父节点相同层的其他节点，但是接下来再次出队头结点，慢慢的就会把父节点所在的一层遍历完成。当遍历完成之后，下一层也按照顺序依次入队了。那我们需要做的，就是依次出队访问就可以了，就可以实现层序遍历。

/**
* 层序遍历
*/
public void LevelOrderTraversal(){
    //如果根节点是空的，说明二叉树就是空的，那就没必要遍历了，直接返回即可。
    if(rootNode == null) return;

    Queue<Node<Type>> queue = new LinkedList<>();//因为队列里存放的是节点，泛型是节点类型Node<Type>，java里的队列继承的是LinkedList。

    queue.offer(rootNode);//入队根节点

    while (!queue.isEmpty()){
        Node<Type> currentHeadNode = queue.poll();//出队队列的头结点，并拿到这个节点的数据
        System.out.println(currentHeadNode.element);//访问，这里只采用打印的访问

        if(currentHeadNode.leftChildNode != null){
            queue.offer(currentHeadNode.leftChildNode);//出队的队头节点的左子节点不为空，就立刻入队
        }
        if(currentHeadNode.rightChildNode != null){
            queue.offer(currentHeadNode.rightChildNode);//出队的队头节点的右子节点不为空，就立刻入队
        }

    }

}

几个程序细节：java的队列是基于链表实现的，因此需要new LinkedList；入队用offer，出队用poll；出队那一刻可以拿到队头元素，没必要使用peek拿。

程序执行的结果是正确的。

遍历接口的设计

上面我们实现了四种遍历方式，但是我们仅仅是对二叉树中的元素进行值打印而已，并没有拿到真实的节点数据。换句话说，我们上面把遍历目前写死了，万一我想要遍历的过程中把所有节点数据都+1呢？所以，遍历接口应该是灵活的，不应该是写死在函数中的。

首先，我们在BinarySearchTree类里声明一个接口Visitor，并在接口里声明一个visit函数，传入的参数就是元素值，将来我们可以在visit的实现里自定义访问规则。

package com.xhb;

public class BinarySearchTree<Type> {

	//.....
	
    public static interface Visitor<Type>{
        void visit(Type element);
    }
    
    //.....
}

这时候，我们就要在遍历函数（以层序遍历为例）中导入这个接口，并把接口函数嵌入进去。

具体的实现规则是：需要一个接口对象作为函数的入口参数，然后在函数内部利用接口对象调用接口函数，进而把元素值传入到接口函数中

/**
 * 层序遍历
 */
public void LevelOrderTraversal(Visitor<Type> visitor){
    //如果根节点是空的，说明二叉树就是空的，那就没必要遍历了，直接返回即可。
    //如果访问器是空的，那说明根本没有访问需求，也不需要遍历了
    if(rootNode == null || visitor == null) return;

    Queue<Node<Type>> queue = new LinkedList<>();//因为队列里存放的是节点，泛型是节点类型Node<Type>，java里的队列继承的是LinkedList。

    queue.offer(rootNode);

    while (!queue.isEmpty()){
        Node<Type> currentHeadNode = queue.poll();

        //调用接口函数visit，并传入参数，然后在外部决定如何使用currentHeadNode.element
        visitor.visit(currentHeadNode.element);
        //System.out.println(currentHeadNode.element);

        if(currentHeadNode.leftChildNode != null){
            queue.offer(currentHeadNode.leftChildNode);
        }
        if(currentHeadNode.rightChildNode != null){
            queue.offer(currentHeadNode.rightChildNode);
        }

    }


}

而到了调用函数的时候，需要传一个接口对象，并且需要指定泛型的类型，并且现场实现接口函数。这就叫函数式接口编程，是某种设计模式，但是我不知道是啥设计模式，可能是策略模式。

public static void main(String[] args) {

   Integer data[] = new Integer[]{7, 4, 9, 2, 5, 8, 11, 3,10, 12, 1};


   BinarySearchTree<Integer> bst = new BinarySearchTree<>();
   for (int i = 0; i < data.length ; i++) {
       bst.add(data[i]);
   }

   bst.LevelOrderTraversal(new BinarySearchTree.Visitor<Integer>() {
       @Override
       public void visit(Integer element) {
           //这里面写visit的访问逻辑
           System.out.print("_" + element);
       }
   });

}

函数的入口参数其实是这么一堆东西：

new BinarySearchTree.Visitor<Integer>() {
    @Override
    public void visit(Integer element) {
        //这里面写visit的访问逻辑
        System.out.print("_" + element);
    }
}

在外部声明接口对象的时候，自动就要实现接口函数，这里我自定义访问规则（每个元素前面加一个下划线，并且不换行打印）。结果如下：

总结一下这种函数式接口设计模式的好处：外界实现遍历逻辑，从而替代内部写死遍历逻辑。具体的执行过程：

1、在二叉树类里声明Visitor接口类，并且声明接口函数
2、将接口函数嵌入到层序遍历的函数中，并且把想要访问的元素以入口参数的形式传给接口函数
3、外部调用遍历函数，需要传接口对象，并且立马实现接口函数
4、接口函数的入口参数就是节点的element，正好对应遍历函数中的调用visitor.visit(currentHeadNode.element);

再实现一下后续遍历PostOrderTraversal：

/**
 * 后序遍历
 */
public void PostOrderTraversal(Visitor<Type> visitor){
    PostOrderTraversal(rootNode,visitor);
}

private void PostOrderTraversal(Node<Type> node,Visitor<Type> visitor){
    if(node == null || visitor == null) return;

    PostOrderTraversal(node.leftChildNode,visitor);
    PostOrderTraversal(node.rightChildNode,visitor);
    visitor.visit(node.element);
}

调用的时候，还是只传visitor，因为我在二叉树类中已经封装好了。

public static void main(String[] args) {

    Integer data[] = new Integer[]{7, 4, 9, 2, 5, 8, 11, 3,10, 12, 1};


    BinarySearchTree<Integer> bst = new BinarySearchTree<>();
    for (int i = 0; i < data.length ; i++) {
        bst.add(data[i]);
    }

    bst.PostOrderTraversal(new BinarySearchTree.Visitor<Integer>() {
        @Override
        public void visit(Integer element) {
            //这里面写visit的访问逻辑
            System.out.print("_" + element);
        }
    });
}

前序遍历和中序遍历同理，这里就不实现了。

遍历的应用

• 前序遍历：树状结构展示
• 中序遍历：二叉搜索树的中序遍历按升序或者降序处理节点
• 后序遍历：适用于一些先子后父的操作
• 层序遍历：计算二叉树的高度；判断一棵树是否为完全二叉树

计算二叉树的高度（使用层序遍历）

• 递归做法

核心思路就是：二叉树的高度就是根节点的高度。我们声明一个求任意一个节点的高度的函数，然后每一个节点的高度都是右子节点或者左子节点中最高的那个再加1。

/**
 * 返回根节点的高度，那就是整个二叉树的高度
 * @return
 */
public int height(){
    return height(rootNode);
}

/**
 * 获取某一个节点的高度
 * @param node
 * @return
 */
private int height(Node<Type> node){
    //如果递归的null节点就返回0
    if(node==null) return 0;
    //某一个节点的高度就等于左右子节点高度最大的那个再加1
    return 1 + Math.max(height(node.leftChildNode),height(node.rightChildNode));
}

调用的时候，直接调用height的方法打印即可。

Integer data[] = new Integer[]{7, 4, 9, 2, 5, 8, 11, 3,10, 12, 1};

BinarySearchTree<Integer> bst = new BinarySearchTree<>();
for (int i = 0; i < data.length ; i++) {
    bst.add(data[i]);
}

System.out.println(bst.height());//4

• 非递归做法（利用层序遍历）

使用层序遍历的核心思想就是遍历完一层，高度+1，遍历完所有层，高度也就出来了。

最关键的一点：怎么知道遍历完一层了？

继续细分：想知道是不是遍历完一层，就需要知道一层有多少个节点。

继续细分：怎么知道一层有多少个节点呢？

想想是不是这么一回事：当弹出第i层最后一个节点的时候，第i+1层已经全部入队了？那么第i+1层的节点个数，不就是队列的size嘛！！

因此需要有一个变量记录着每一层节点的个数，且在弹出一个节点后立马 -1。当这个变量等于0的时候，说明第i层的节点全部弹出完毕，这个变量就要记录第i+1层的个数，同时height++。直到队列为空，也就是最后一层的节点也全部弹出了。

实现如下：

/**
 * 采用层序遍历求出二叉树的高度
 * @return
 */
public int heightLevelOrder(){

    if(rootNode == null) return 0;

    //访问完一层，height就要++。那怎么确定访问完一层呢，首先需要知道这一层有多少元素，高度是访问完当前层再加1，因此初始是0
    int height = 0;
    //记录当前层节点的个数，走到这，根节点指定是存在的，因此初始个数是一个
    int levelSize = 1;

    Queue<Node<Type>> queue = new LinkedList<>();

    queue.offer(rootNode);

    while (!queue.isEmpty()){
        Node<Type> currentNode = queue.poll();
        //每当poll一个节点，当前层节点的个数就要-1
        levelSize--;

        if(currentNode.leftChildNode != null){
            queue.offer(currentNode.leftChildNode);
        }
        if(currentNode.rightChildNode != null){
            queue.offer(currentNode.rightChildNode);
        }

        //出队完当前层的最后一个元素时，下一层其实已经全部入队了，那下一层有多少个节点，只需要查看队列中的元素个数即可
        if(levelSize == 0){
            //说明，当前层访问完毕了，该访问下一层了，所以levelSize要更新为下一层的个数
            levelSize = queue.size();
            //当前层访问完了，说明已经捕获了二叉树的高度+1
            height++;
        }
    }

    return height;
}

几个关键点：height记录高度，初始值为0，因为height想要++的条件是访问完当前层之后，初始的时候根节点并没有被弹出，因此height的初始值为0。levelSize记录当前层多少个节点，初始值为1。因为能执行到这一句，说明根节点不为空，第一层有一个节点，随着不断地弹出，levelSize不断地--。当levelSize=0时，说明当前层已经全部从队列中出队了，那就要访问下一层了，levelSize需要更新为下一层的节点个数。访问完当前层，height就要++。

main函数直接调用，即可打印

Integer data[] = new Integer[]{7, 4, 9, 2, 5, 8, 11, 3,10, 12, 1};

BinarySearchTree<Integer> bst = new BinarySearchTree<>();
for (int i = 0; i < data.length ; i++) {
    bst.add(data[i]);
}

System.out.println(bst.heightLevelOrder());//4

判断一棵树是否为完全二叉树（使用层序遍历）

首先要非常清晰地了解完全二叉树的性质。一个二叉树，得具备什么特点，才能叫完全二叉树？

特点：叶子节点只会出现在最后两层，且最后一层的叶子节点都靠左对齐，就像下图一样：

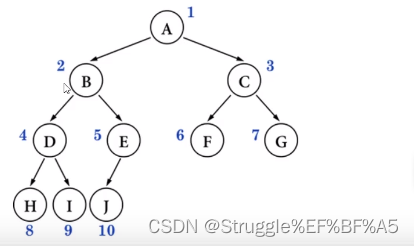
为什么要使用层序遍历呢？因为完全二叉树符合层序遍历的逻辑，从上到下，从左到右的遍历。

判断一棵树是不是完全二叉树，无非就是一下几种情况：

• 如果树为空，那就返回false
• 如果树不为空，那就开始层序遍历二叉树，也会有以下几种情况：
  1、如果node.left != null && node.right != null 时，那就将node的左右节点入队
  2、如果node.left == null && node.right != null 时，说明某一个节点在没有左子节点的情况下还存在右子节点，那就不符合完全二叉树的性质，此时可以直接返回false，不用继续遍历了
  3、如果node.left != null && node.right == null 时，或者node.left == null && node.right == null 时，这种情况下说明某一个节点度为1且靠左对齐，或者遍历到度为0的节点了，此时接下来所有节点，必须必须都是叶子节点，否则就不符合完全二叉树的性质了。

实现代码如下，其中几处技术细节，需要注意：
1、三个判断必须要梳理好，什么条件干什么事
2、最后一个判断需要注意一个最关键的点，那就是要求一旦符合最后一个条件，说明接下来遍历的节点必须都得是叶子节点。这个该怎么实现呢？这里用了一个非常巧妙的标志位，isLeaf 。在循环遍历之前，先将isLeaf 置位false。一旦触发最后一个条件，那说明接下来的所有节点遍历结果都必须是叶子节点，此时我们将isLeaf 置位true，意味着要求接下来的遍历都必须遍历出叶子节点才能继续往下遍历。
3、然后，我们就在遍历节点的下方做一个判断，判断条件是：要求是叶子节点（isLeaf == true）的情况下，如果该节点不是叶子节点，等同于(currentNode.leftChildNode != null || currentNode.rightChildNode != null) == true，就进入if语句，返回false。这真的是一个非常非常巧妙的设计，也是解题的关键。

/**
 * 判断是否是完全二叉树
 * @return
 */
public boolean isComplete(){

    Queue<Node<Type>> queue = new LinkedList<>();
    queue.offer(rootNode);

    boolean isLeaf = false;//先把是否要求接下来都是叶子节点的标志位置false，表示目前不要求
    while (!queue.isEmpty()){
        Node<Type> currentNode = queue.poll();
        //遍历判断，如果要求是叶子节点isLeaf = true，但是当前的节点不是叶子节点，那就返回false
        if(isLeaf && (currentNode.leftChildNode != null || currentNode.rightChildNode != null)){
            return false;
        }

        if(currentNode.leftChildNode != null && currentNode.rightChildNode != null){
            queue.offer(currentNode.leftChildNode);
            queue.offer(currentNode.rightChildNode);
        }

        if(currentNode.leftChildNode == null && currentNode.rightChildNode != null){
            return false;
        }

        if((currentNode.leftChildNode !=null && currentNode.rightChildNode == null) || (currentNode.leftChildNode ==null && currentNode.rightChildNode == null)){
            //接下来遍历的节点必须都得为叶子节点，否则就返回false
            isLeaf = true;//置位true，表示接下来遍历的节点都得是叶子节点了
        }


    }

    //遍历完都没有返回false，说明此二叉树通过了考验，返回true，证明这是一棵完全二叉树
    return true;
}

但是，其实上述代码是存在一处bug的。比如下面的二叉树，当我遍历到4时，满足最后一个条件，接下来只判断后面的节点是不是叶子节点即可，并没有把子节点2入队。所以遍历到9队列也就空了，我就会判断这是一个完全二叉树。但是，这并不是一个完全二叉树，因为不满足叶子节点只出现在最后两层。

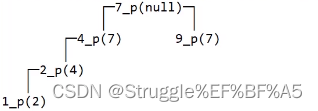
造成这样的bug，问题出现在哪呢？

是因为，我们入队节点的条件是，某个节点同时存在左子节点和右子节点，才会把两个子节点入队。当只有一个子节点时，是没有入队操作的，这是不对的。因此修正bug后的代码如下：

public boolean isComplete(){

    Queue<Node<Type>> queue = new LinkedList<>();
    queue.offer(rootNode);

    boolean isLeaf = false;//先把是否要求接下来都是叶子节点的标志位置false，表示目前不要求
    while (!queue.isEmpty()){
        Node<Type> currentNode = queue.poll();
        //遍历判断，如果要求是叶子节点isLeaf = true，但是当前的节点不是叶子节点，那就返回false
        if(isLeaf && (currentNode.leftChildNode != null || currentNode.rightChildNode != null)){
            return false;
        }

        if(currentNode.leftChildNode != null && currentNode.rightChildNode != null){
            queue.offer(currentNode.leftChildNode);
            queue.offer(currentNode.rightChildNode);
        } else if(currentNode.leftChildNode == null && currentNode.rightChildNode != null){
            return false;
        }else {
            //接下来遍历的节点必须都得为叶子节点，否则就返回false
            isLeaf = true;//置位true，表示接下来遍历的节点都得是叶子节点了
            //在这个条件下，存在左子节点的情况，需要把此时的左子节点入队，否则就会出现bug
            if(currentNode.leftChildNode !=null){
                queue.offer(currentNode.leftChildNode);
            }
        }
        
    }
    //遍历完都没有返回false，说明此二叉树通过了考验，返回true，证明这是一棵完全二叉树
    return true;
}

注意：我把三个if合并了，因为本来就囊括所有条件了。

翻转二叉树（四种遍历方法都可）

翻转二叉树其实就是把所有节点的左右子节点都交换。最直观的思路就是，遍历每一个节点，并同时交换左右子节点。

• 前序遍历实现交换，采用递归的形式

/**
 * 翻转节点node左右子树,采用前序遍历实现
 * @param node
 */
public Node<Type> invertTree(Node<Type> node){
    if(node == null) return node;

    Node<Type> tempNode = node.leftChildNode;
    node.leftChildNode = node.rightChildNode;
    node.rightChildNode = tempNode;

    invertTree(node.leftChildNode);
    invertTree(node.rightChildNode);

    return node;
}

有人会问了，左右交换完了，下面的node.leftChildNode不就是右子节点了嘛，node.rightChildNode不就变成了左子节点了嘛。我想说，对的，确实变了。但是前序遍历不一定要求非得先遍历左然后再遍历右，只要保证最先遍历根节点就行。后序遍历也不需要变。

但是，如果是采用中序遍历实现，就不一样了。就必须注意变换左右之后，最后还要使用leftChildNode变量。以下是中序遍历实现翻转

/**
 * 翻转节点node左右子树,采用中序遍历实现
 * @param node
 */
public Node<Type> invertTree(Node<Type> node){
    if(node == null) return node;
    
	invertTree(node.leftChildNode);
	
    Node<Type> tempNode = node.leftChildNode;
    node.leftChildNode = node.rightChildNode;
    node.rightChildNode = tempNode;

    invertTree(node.leftChildNode);

    return node;
}

层序遍历也是很简单，原则就是对遍历得到的节点做一些处理（交换其左右子节点）

public Node<Type> invertTree(Node<Type> node){
    if(node == null) return node;

    Queue<Node<Type>> queue = new LinkedList<>();
    queue.offer(rootNode);

    while (!queue.isEmpty()){
        Node<Type> currentHeadNode = queue.poll();

        Node<Type> tempNode = currentHeadNode.leftChildNode;
        currentHeadNode.leftChildNode = currentHeadNode.rightChildNode;
        currentHeadNode.rightChildNode = tempNode;

        if(currentHeadNode.leftChildNode != null){
            queue.offer(currentHeadNode.leftChildNode);
        }
        if(currentHeadNode.rightChildNode != null){
            queue.offer(currentHeadNode.rightChildNode);
        }

    }

    return node;
}

根据遍历结果重构二叉树

以下遍历结果可以保证重构出唯一的一棵二叉树

• 前序遍历 + 中序遍历
• 后序遍历 + 中序遍历

我们举一个例子，就知道为什么给出两个遍历结果，就可以还原二叉树的样子了。

假设前序遍历：4 2 1 3 6 5
中序遍历结果：1 2 3 4 5 6

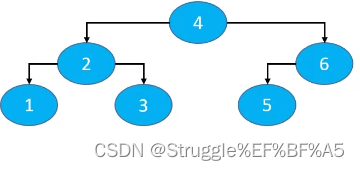
根据前序遍历结果可知，4是根节点；根据中序遍历结果和4是根节点可知，1,2,3是左子树，5,6是右子树；所以在前序遍历中，2,1,3是左子树，6,5是右子树；根据前序遍历的特点，左右子树也是前序遍历可是，2是左子树的根节点，6是右子树的根节点；那么，在中序遍历结果左子树1,2,3中，2是根节点，1是左子节点，2是右子节点；在右子树5,6中，6是根节点，5那就是左子节点。

至此，二叉树还原成功。

• 只知道前序遍历结果和后续遍历结果，能否重构出唯一的一棵二叉树呢？

这里有一个条件，那就是如果它是一棵真二叉树（节点的度要么为2要么为0，也就是说节点要么左右子节点同时存在，要么都不存在），结果是唯一的。其他情况没法判断。

为什么呢？

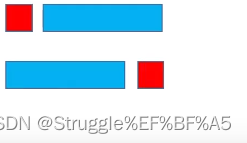
因为，如果不是真二叉树，可能根节点只有左子树没有右子树，或者只有右子树没有左子树。这种情况下，没法判断蓝色部分是左子树还是右子树。因为我们根据遍历结果重构二叉树一个关键的步骤就是找到左子树区间和右子树区间。如果不确定是真二叉树的情况下，那就没法确定左右子树区间。

假如，我们知道了，它就是一棵真二叉树，也就意味着根节点要么没有左右子树，要么左右子树都存在。既然我们确定左右子树都存在，那就可以划分左右子区间。比如下图：

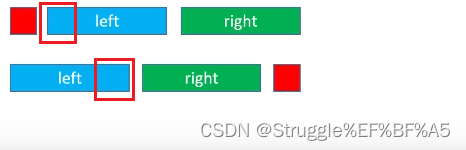
红色框部分就是左子树的根节点，根据这个就能把区间区分开，也就能把二叉树重构出来了。

前驱节点（predecessor）

前驱节点的概念针对所有二叉树。某个节点的前驱节点就是中序遍历的前一个节点。记住，一定是中序遍历条件下的前一个节点。

我们最常用的还是二叉搜索树，因此，在二叉搜索树中，前驱节点就是前一个元素值比它小的节点。下面我们以二叉搜索树为例，实现一下给定任意节点，可以返回前驱节点的函数。

思考：二叉搜索树的特点是：左 < 父 < 右。

因此某一个节点，如果左子树不为空，那么前驱节点一定在左子树中，而且是左子树中最右边的节点（对于左子树来说，最大的节点一定是最右边的）

所以，我们在node.left != null的情况下，predecessor = node.left.right.right…，终止条件是right ==null，说明这是最右的一个节点了。

万一某个节点的左子树为空呢？前驱节点该怎么找？比如下图的5节点，没有左子树。很容易发现4是前驱节点，那怎么找呢？

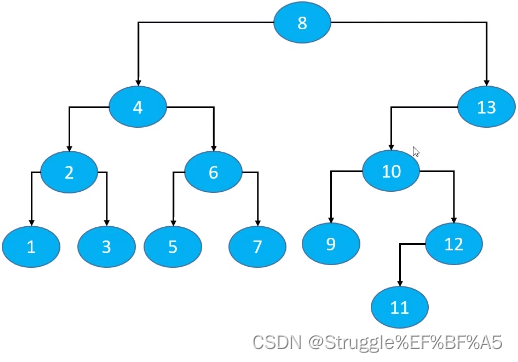
结论：当一个节点没左子树时，且父节点不为空，就要向上找，直到遇到变成右子树的时候，停下来。什么叫变成右子树呢。

举例5节点，5找到父节点6，5是6的左子树，6继续找父节点4，发现6是4的右子树了，这就叫变成了右子树。5的前驱节点是4

举例9节点，也是这样，没有左子树，但是有父节点。向上找，遇到10，9是10的左子树，再向上找遇到13,10是13的左子树，在向上找遇到8,13是8的右子树。哎！这就变成右子树了，停下来。9的前驱节点是8

举例7节点，也没有左子树，向上找发现7就是6的右子树，立马停下。7的前驱节点是6

举例1节点，没有左子树，一直向上找直到找到根节点，都没有遇到右子树，然后根节点向上找，发现是空的，这种情况就是没有前驱节点的情况。

为什么遇到变成右子树时停下来，就能立马找到前驱节点呢？因为，该节点没有左子树，也就意味着不能立马判断前驱节点是谁。只能向更更更上的方向去找，找到该节点所处的位置是某个节点的右子树时立马停下来，说明某个节点的下一个节点就是该节点了。

总结就是，当node.left==null && node.parent !=null时，predecessor = node.parent.parent.parent…，直到node处于parent的右子树中立马停下，说明恰好找到中序便利时，node的前一个遍历节点，即前驱节点。

所有的条件可以归结为下方：

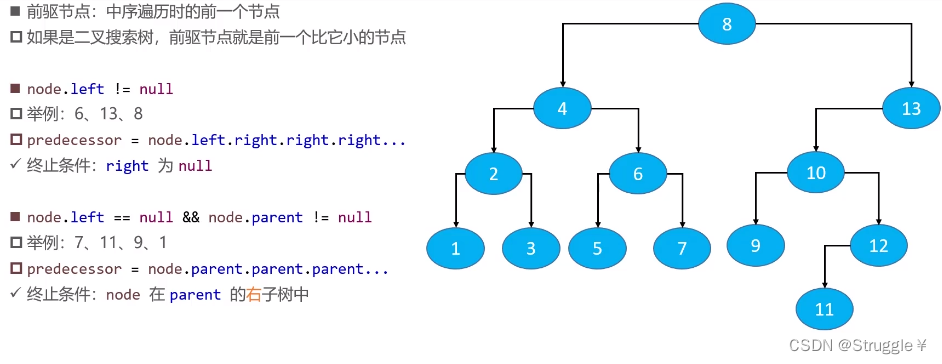
还有一种情况，那就是，左子节点是空的，且父节点也是空的。比如根节点8（假设左子树现在不存在），这种情况下就没有前驱节点。

代码实现如下：

/**
 * 返回给定节点node的前驱节点
 * @param node
 * @return
 */
public Node<Type> predecessor(Node<Type> node){
    if(rootNode==null) return null;

    //如果左子树不为空，说明前驱节点一定在左子树中，并且是左子树最右边的节点
    if(node.leftChildNode != null){
        Node<Type> predecessorNode = node.leftChildNode;//默认前驱是左子节点
        while (predecessorNode.rightChildNode != null){
            //如果predecessorNode的右子节点不为空，继续找
            predecessorNode = predecessorNode.rightChildNode;
        }
        //跳出循环时，predecessorNode的右子节点为空，说明不能继续向右查找了，那么当前的predecessorNode就是最右，也就是我们要找的前驱节点
        return predecessorNode;
    }

    //如果左子树为空，说明该节点的前驱节点是从父节点的方向传来的，就要向父节点找
    //而且这个前驱节点一定会把node视为右子树中的一个节点，因为只有视为右子树上的节点，才是先访问前驱，再访问node
    if(node.leftChildNode == null && node.parentNode != null){
        while (node == node.parentNode.leftChildNode && node.parentNode != null){
            node = node.parentNode;
        }
    }

    //能来到这，说明下面两个条件有一个成立了,一个是node向上parent为null了，一个是遇到成为右子树的节点了
    //node.parentNode == null
    //node == node.parentNode.rightChildNode
    //此时node.parentNode就是前驱节点

    return node.parentNode;
}

后继结点（successor）

跟前驱节点相反，中序遍历时的后一个节点叫做当前节点的后继节点。（如果是二叉搜索树，后继节点就是后一个比它大的节点）

检索的方式跟前驱节点也是相反的。

后继节点的实现跟前驱节点的区别就是，把前驱节点中的所有left改成right，所有right改成left，就完成了。

/**
 * 返回给定节点node的后继节点
 * @param node
 * @return
 */
public Node<Type> successor(Node<Type> node){
    if(rootNode==null) return null;

    //如果左子树不为空，说明前驱节点一定在左子树中，并且是左子树最右边的节点
    if(node.rightChildNode != null){
        Node<Type> successorNode = node.rightChildNode;//默认前驱是左子节点
        while (successorNode.leftChildNode != null){
            //如果predecessorNode的右子节点不为空，继续找
            successorNode = successorNode.leftChildNode;
        }
        //跳出循环时，predecessorNode的右子节点为空，说明不能继续向右查找了，那么当前的predecessorNode就是最右，也就是我们要找的前驱节点
        return successorNode;
    }

    //如果左子树为空，说明该节点的前驱节点是从父节点的方向传来的，就要向父节点找
    //而且这个前驱节点一定会把node视为右子树中的一个节点，因为只有视为右子树上的节点，才是先访问前驱，再访问node
    if(node.rightChildNode == null && node.parentNode != null){
        while (node == node.parentNode.rightChildNode && node.parentNode != null){
            node = node.parentNode;
        }
    }

    //能来到这，说明下面两个条件有一个成立了,一个是node向上parent为null了，一个是遇到成为右子树的节点了
    //node.parentNode == null
    //node == node.parentNode.rightChildNode
    //此时node.parentNode就是前驱节点

    return node.parentNode;
}

平衡二叉搜索树

一个例子，说明为什么要搞平衡二叉搜索树。

如下图所示是一个二叉搜索树（我们按照7,4,9,2,5,8,11的顺序依次添加元素，就可以得到这样一个二叉搜索树），假如我要进行搜索，添加，删除某一个元素，最多需要比较三次节点就可以找到对应的位置。这就是二叉搜索树的高效之处。

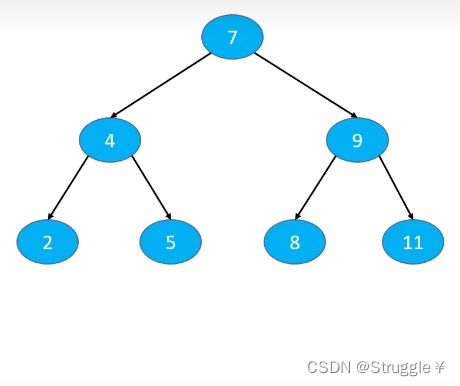
添加，删除，搜索的最坏时间复杂度只跟树的高度有关，并不是根据元素数量有关。这对比链表，数组就是高效之处。

但是，如果我们在添加元素时，没有按照比较好的顺序添加，可能就会出现下图所示的二叉搜索树。如果在这种二叉搜索树下进行添加，删除，搜索。那最坏时间复杂度就是节点个数了，跟链表没什么区别了就。

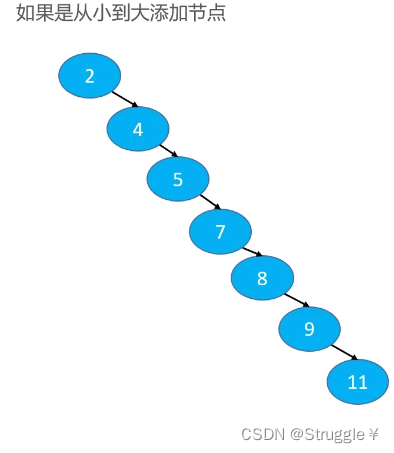
总结，第一个二叉树貌似很平衡（左子树和右子树的高度差不多），第二个二叉树很不平衡。所以，我们要尽量的让二叉搜索树平衡一些，这就是平衡二叉搜索树存在的意义。

添加，删除节点时，都有可能导致二叉搜索树退化成链表，那有没有什么办法防止二叉搜索树退化成链表呢？话句话是，如何构建一个平衡二叉搜索树呢？

平衡的概念（Balance）

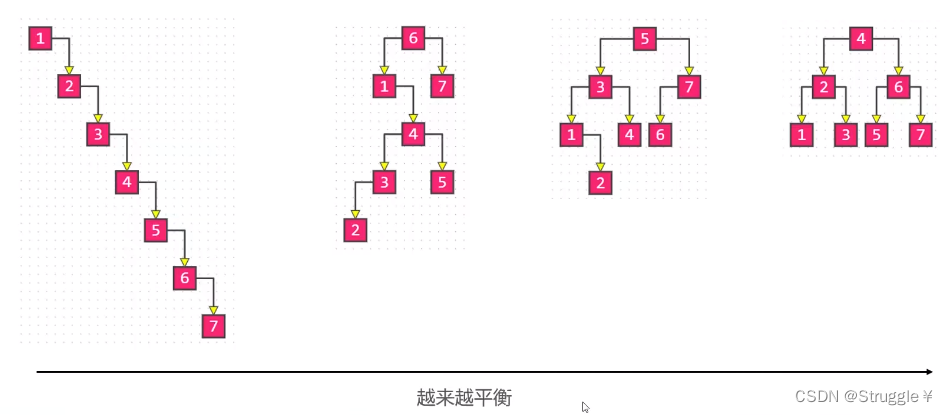
在二叉搜索树中所谓平衡，就是当节点总数量固定时，左右子树的高度越接近，这棵二叉树就越平衡。（也就是二叉树的总高度相对越低）

下图给出了这种示意，同样是7个节点的情况下，从左到右，越来越平衡

如何改进二叉搜索树到AVL树

首先，节点的添加和删除是从根本上影响二叉搜索树的平衡。但是，节点的添加和删除的顺序是无法限制的，可以认为是随机的。（因为，二叉搜索树设计出来是给调用者使用的，不可能限制添加的顺序和删除的顺序）

所以，我们改进的方向是：在节点添加或者删除之后，想办法让此时的二叉搜索树恢复平衡（即减小树的高度）

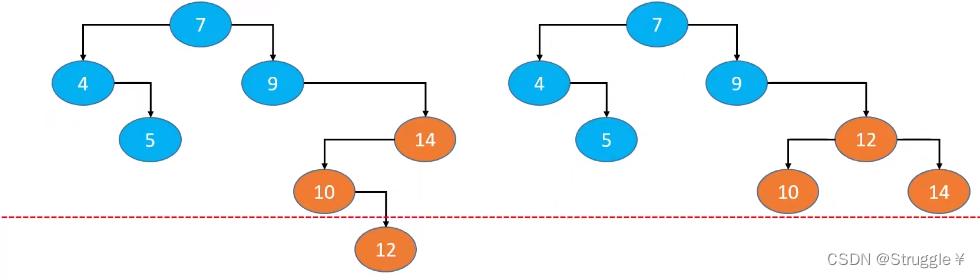
比如下图的左边是初始二叉搜索树，右边改进：调整了橙色节点的父子关系，使得左右子树的高度差减少。在调整了橙色节点父子关系之后，二叉搜索树的性质没有变，不会破坏原有的节点关系。

如果继续调整节点的位置，完全可以达到理想平衡（调整成一个完全二叉树都是没有问题的），但是付出的代价可能比较大。比如调整的次数过多，反而增加了时间复杂度。

总结来说：比较合理的改进方案是：用尽量少的调整次数达到适度平衡即可。那么一棵达到适度平衡的二叉搜索树，也就是平衡二叉搜索树。

常见的平衡二叉搜索树（Balance Binary Search Tree）都有哪些呢？下面列举了两个最常见的：

• AVL树：Windows内核中广泛使用
• 红黑树：C++中的STL库（map，set），Java中的TreeMap TreeSet、HashMap、HashSet

AVL树（实现AVL树）

AVL树的名字取自两个发明者的首字母，并不是某某的缩写。

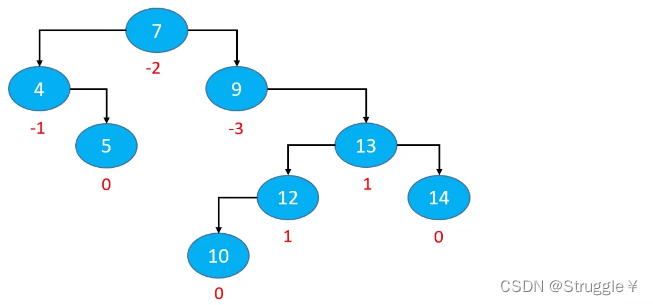
AVL中有一个很重要的概念：平衡因子（Banlance Factor），表示某节点的左右子树的高度差（左子树高度减去右子树高度）。

如下图所示，给出了每个节点的平衡因子

AVL树的特点

AVL树要求，每个节点的平衡因子只可能是1,0，-1（绝对值小于等于1，如果超过1，那这棵树被认为失衡），换句话说，每个节点的左右子树的高度差不能超过1。此时，AVL树可以办到，搜索、添加、删除的时间复杂度维持在o(logn）级别。

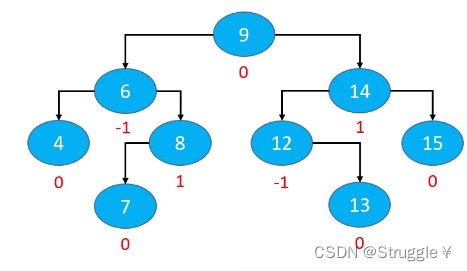
比如下图就是一棵AVL树：

假设我们按照顺序，依次添加节点就会得到一个左图的普通二叉搜索树，经过改进，我们可以得到右图的AVL树：

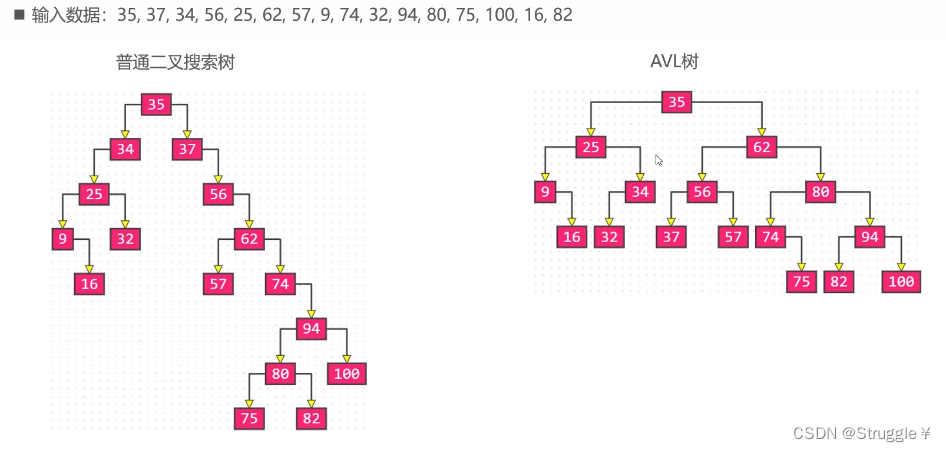
怎么办到的呢？怎么改进的呢，我们接下来会解释。我们先了解一下，添加或者删除怎么导致的失衡。

添加导致的失衡

假设二叉搜索树的原始样子如下图所示：可以看到这是一棵AVL树，因为每个节点的平衡因子的绝对值都小于等于1。

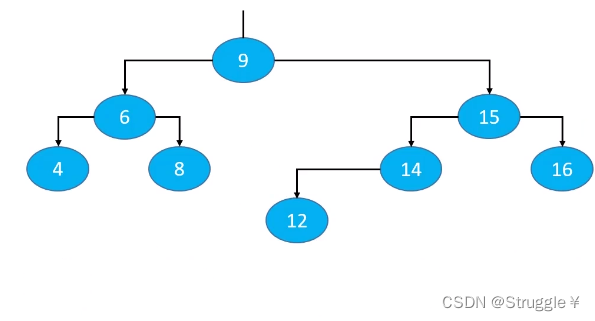
此刻，我添加一个13进去，发现14节点，15节点，9节点都发生了失衡现象。而且细心点可以发现，失衡的都是祖父节点（父节点的父节点以及以上节点，父节点是不会失衡的）。所以最坏的情况就是可能会导致所有的祖先节点都失衡，而父节点和非祖先节点都不可能失衡。

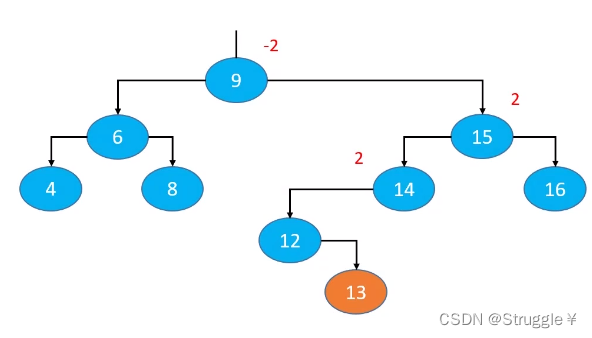
既然我们知道了，只有祖先节点可能失衡（但并不是说所有的祖先节点都失衡，有可能只有一个失衡，也有可能都不失衡），那我们就可以针对性的去解决。

LL-右旋转策略

失衡节点跟添加位置的节点是Left-Left的关系，就叫LL关系，紧接着要对失衡节点进行右旋转，所以才叫LL-右旋转。

先解释这个图里面的元素：首先这只是某个二叉搜索树里的一个局部，因为g上面有一个线表示g也是某个节点的子节点。n有左右子树，分别是T0和T1（至于T0和T1是啥样的，无所谓，可能是空的，也可能很多节点），p有左右子树，g也有左右子树。

为什么只把n、p、g单独画出来呢？因为我们在某个节点添加新节点时，只有祖父节点可能会失衡，也就是说只需要画出三个节点，就可以解释所有情况。n表示node，p表示parent，g表示grandparent。

黑色虚线和红色虚线表示高度差1。以目前的情况来看，n、p、g都没有失衡，都满足AVL树的要求。

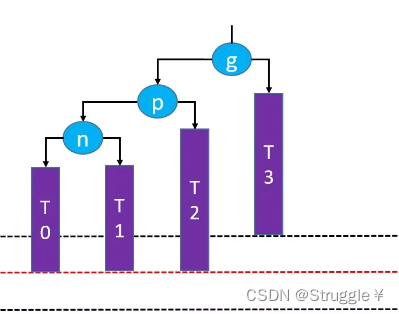
此时，我新添加一个节点再T0上（红色方块），发现n和p也没有失衡，但是g点失衡了（不要纠结如果T2的高度减少1，p也失衡的情况。因为如果那样的情况p和g都失衡，需要一个一个解决，p的解决方案跟此时的g是一样的）。现在就是g失衡了，怎么办吧。

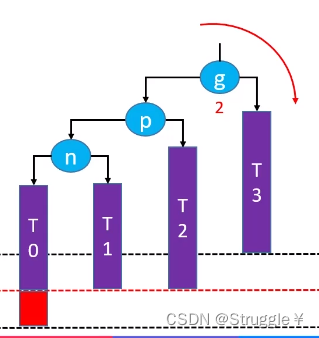
我们的做法是对失衡节点g进行右旋转（因为失衡节点与新添加节点的关系是LL），右旋转g需要完成哪些操作呢？

g.left = p.right//让g的左子节点指向p的右子节点
p.right = g //然后让p的右子节点指向g
让p成为这棵子树的根节点//最后让p变成这棵子树的根节点

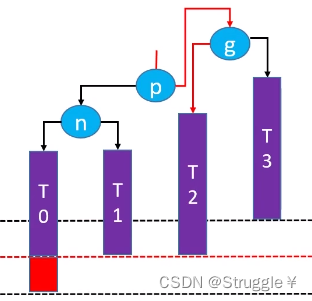
把上面的图捋顺，就可以得到下面的图，可以很清晰的看到，稍微平衡了一些（g本来不平衡的，现在变成平衡了），而且还不影响原有二叉搜索树的关系。

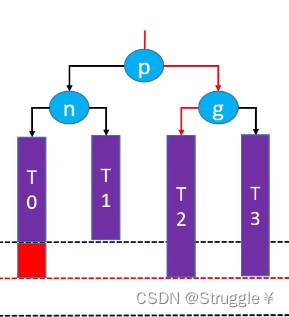
变换之后，我们把所有的指向都弄对了。但是，有些节点在变换之后，其父节点变了（比如说T2的父节点由p变成g，g的的父节点也变成了p，p的父节点也变成了之前g的父节点），因此我们要维护一下节点的parent属性。

除此之外，因为p和g的位置发生了变化，因此他们的高度也要在变换后更新（高度是计算平衡因子的基础，因此每个节点的高度属性很重要）

这些都会在代码中体现！

RR-左旋转策略

根据前面的经验，这个RR指定是表示失衡节点和插入节点的关系是Right-Right的关系，并且要对失衡节点进行左旋转。

如下图所示，n是g的RR节点，当插入新结点在n上时，g的平衡因子变成了-2，失衡了。因此要多g进行左旋转，

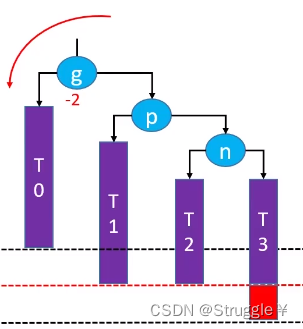
左旋转干的事就是干了下面三个操作

g.right= p.left//让g的左子节点指向p的右子节点
p.left= g //然后让p的右子节点指向g
让p成为这棵子树的根节点//最后让p变成这棵子树的根节点

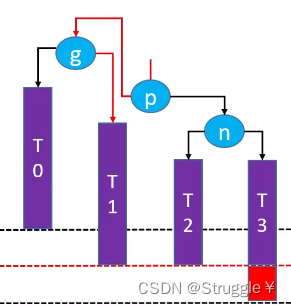
捋顺一下，变成如下：整棵树都恢复平衡

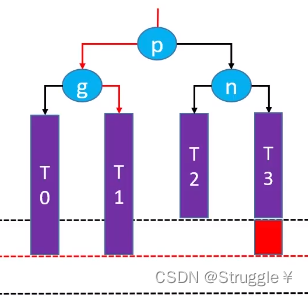
跟LL-右旋转一样，要维护T1，g，p的parent属性（原则就是谁的parent变换，就维护谁）。同时更新g和p的高度。

LR-左旋转+右旋转

看名字也能感觉出来是什么意思。失衡节点和插入节点的关系是Left-Right关系，需要进行两次旋转操作。之前是只对失衡节点进行旋转，这里要对失衡节点和插入节点的父节点进行旋转操作

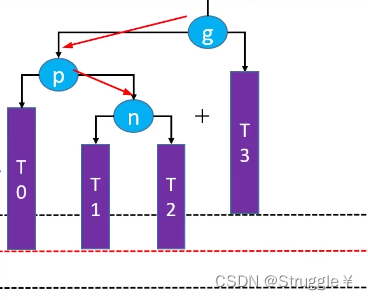
比如，在T2处插入一个节点，就形成了LR的关系，此时g失衡了，如下所示：

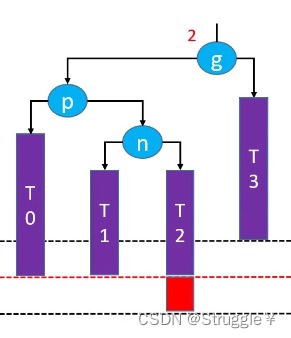
那，左旋转+右旋转是怎么回事呢？

• 先对p点进行左旋转，也就是让p.right = n.left && n.left = p && g.left = n。变成下面的样子：明显回到了LL的情况，T0的高度使得g点失衡了。

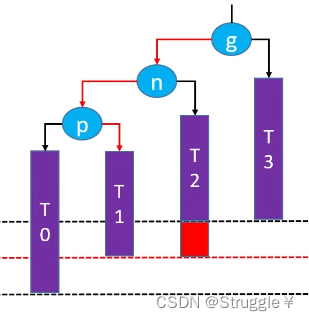
• 然后再对g点进行右旋转，也就是让g.left = n.right && n.left = g && n成为这棵子树的根节点，根据右旋转性质，就变成了下面的情况：

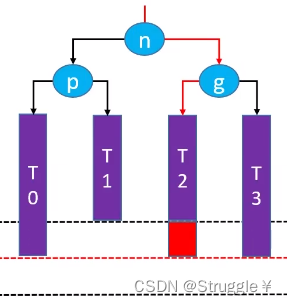
这棵树就保持平衡了，最后别忘了维护parent和高度就行。

RL-右旋转+左旋转

顾名思义，失衡节点和插入节点的关系是Right-Left关系，而且需要进行两次旋转操作。

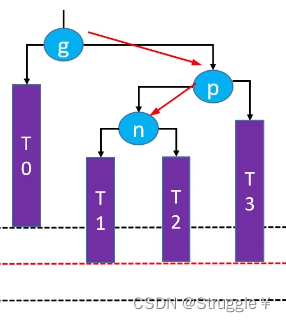
假设，向T1处添加节点，就如下图所示：g的平衡因子变成了-2，失衡了。

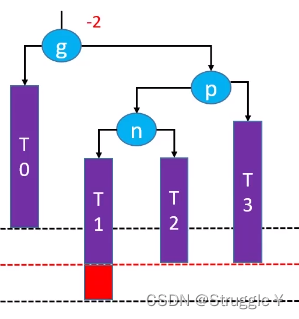
• 因此，先对p进行右旋转（因为插入节点和p是LL关系），旋转之后如下：
  

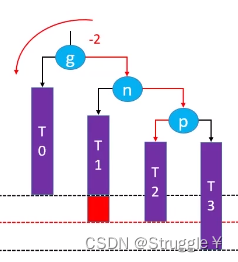
• 再次对g进行左旋转，整棵树都恢复了平衡

最后别忘了维护parent属性和高度属性。

四种情况总结

这四种情况，已经概括了所有可能失衡的情况，记住是所有！！！！不要再找一些特殊情况试图推翻，如果你找到了，那一定是你理解错了。

所以，我们在实现AVL树的时候，只需要判断是四种情况的哪一种，然后做出相应的处理即可。

程序手撕AVL树

先问一个问题啊：什么时候做出调整操作呢？

答案：在添加节点之后，并且检查到有失衡的节点，这时才需要做出调整。

在哪里写实现调整策略？

因为AVL树继承自二叉搜索树，调整策略是AVL树独有的，因此要把调整策略写在AVL树当中。但是，添加节点的实现是写在二叉搜索树当中的。而我们的需求是在添加节点之后实现调整策略，所以好像又得必须写在二叉搜索树中的add方法里。这该怎么办呢？

• BinarySearchTree类中声明一个函数，功能就是新插入一个节点node之后，进行操作。但是在BinarySearchTree类中，函数的实现是空的，意味着什么都不做。

/**
 * 插入节点node之后，进行的操作
 * @param node 新插入的节点
 */
protected void afterAdd(Node<Type> node){ }

• 然后在AVLTree类中重写方法，并实现相应的调整策略。

/**
 * AVL就是一个带有自平衡机制的二叉搜索树，因此可以直接就继承BST
 * @param <Type>
 */
public class AVLTree<Type> extends BinarySearchTree<Type> {

    public AVLTree(){
        this(null);
    }

    public AVLTree(Comparator<Type> comparator){
        super(comparator);
    }

    @Override
    protected void afterAdd(BinarySearchTree.Node<Type> node) {
		//重写
    }
}

• 既然是添加节点之后干的事，需要写在add函数里。因为add函数里只有两处是添加节点的操作，因此只需要在新添加节点处调用即可。这样做可以实现什么功能呢：BinarySearchTree中的afterAdd函数内部实现是空的，意味着普通的二叉搜索树在添加节点之后什么也不干；AVLTree中的afterAdd函数内部实现是有操作的，意味着AVLTree在添加节点之后需要调用AVLTree重写的afterAdd函数，实现相应的操作。

/**
 * 添加元素到二叉搜索树中
 * @param element
 */
public void add(Type element){
    elementNotNullCheck(element);//判断添加的节点的元素值是否为null

    //如果添加的是根节点，意味着此时二叉树是空的
    if(rootNode == null){
        rootNode = new Node<>(element,null);//根节点的父节点就是null，因为没有父节点
        size++;
        
        //添加节点之后干的事
        afterAdd(rootNode);
        
        return;
    }

    //程序能到这，说明二叉树已经存在根节点了，那我们添加的就是普通节点了
    /**
     * 添加节点的步骤：
     * 1、找到该节点的插入位置，也就是找到父节点（这一步是核心步骤）
     * 2、创建该节点
     * 3、判断比父节点大还是比父节点小，从而判断是左子节点还是右子节点
     * 如果遇到值相等的元素，那就覆盖掉原有节点
     */

    //任何节点都是从父节点开始找的，所以首先赋值父节点
    Node<Type> currentNode = rootNode;
    //循环的目的是找到插入节点的父节点，因此需要在循环结束的前一刻拿到父节点，初始默认根节点就是父节点
    Node<Type> parent = rootNode;
    //循环的目的不仅要找到插入节点的父节点，还要知道插在左边还是插在右边，因此方向也要记录,所以把决定方向的变量放在循环外面
    int cmp_result = 0;

    while (currentNode != null){
        //当前节点不为空，才可以继续比较；如果在不断地比较之后，当前节点currentNode等于null，说明不能继续比了，此时就要把传进来的节点插入了
        cmp_result = compareNode(element, currentNode.element);
        parent = currentNode;
        if(cmp_result > 0){
            //说明传进来的element大于当前节点的element，那就得向右子树进行搜索，然后继续比较
            currentNode = currentNode.rightChildNode;

        } else if(cmp_result < 0){
            //说明传进来的element小于当前节点的element，那就得向左子树进行搜索，然后继续比较
            currentNode = currentNode.leftChildNode;

        }else {
            // 说明当前节点的element和传进来的element相等，那就覆盖当前值
            currentNode.element = element;
            return;
        }
    }

    //循环完毕，currentNode一定为空，所以要提前保存插入节点的父节点，还要提取保存插入方向
    //创建该节点，把传进来的element赋值给该节点，因为循环结束就知道父节点是谁了，因此这里直接传入
    Node<Type> newNode = new Node<>(element,parent);
    //判断比父节点大还是比父节点小，从而判断是左子节点还是右子节点
    if(cmp_result > 0){
        //说明该插向右边
        parent.rightChildNode = newNode;
    }else {
        //说明该插向左边
        parent.leftChildNode = newNode;
    }

    size++;//插入完毕后，size要+1

    //添加节点之后干的事
    afterAdd(newNode);

}

这就是，这种设计的巧妙之处，这也是某种设计模式，但是我目前没学，好像是模板模式。将来，我在main函数中new AVLTree，调用的就是AVLTree的函数，这类似于C++中的多态。

实现afterAdd

可以看到，afterAdd函数需要node作为参数。要搞清楚这个node是什么，是哪个节点？

@Override
protected void afterAdd(BinarySearchTree.Node<Type> node) {

}

这个node就是新插入的节点，也就是下图中红色小方块。

要注意，新插入节点导致整棵树失衡，其本质是新插入的节点导致了某一个祖父节点失衡，然后上面的所有祖父节点都可能失衡。因此，想要解决整棵树的失衡问题，只需要找到插入节点那一刻，最先失衡的祖父节点即可。

拿上图为例：新插入节点在T0处，只有g失衡了，g的父节点也可能失衡。但是g的父节点失衡是由于g导致的，如果g恢复了平衡，g的父节点也就恢复了平衡。因此，只需要恢复g点的平衡就可以了（换句话说，只需要把这棵子树恢复平衡就可以了，至于这棵子树恢复之后，谁是根节点无所谓）

对于g的父节点来说，失衡的主要原因是以g为根节点的子树的高度增加了，导致g的父节点的左右子树高度差可能会增加。因此，只需要把这棵子树高度恢复就可以了。如下所示，恢复之后高度变成和原来一样，只不过是根节点变了而已。

这对于二叉搜索树来说，无所谓，只要不破坏二叉搜索树的性质，随便交换节点的位置。

所以，怎么解决呢？顺着插入节点的parent一路向上找，看看是哪个祖父节点最先失衡的，也就是找到了图中的g点。

当然会存在插入节点之后，没有失衡的点，也就是一路向上找parent，最终都变成了null了还没有找到失衡的节点。因此，这里需要一个while循环，不断地找，如果发现当前的node是平衡的，我们做一些事情；如果发现当前的node是失衡的，我们就要修正失衡。因此，代码的初始框架如下：

@Override
protected void afterAdd(BinarySearchTree.Node<Type> node) {
    while ((node = node.parentNode) != null){
        if(node is Balanced){
            //做一些处理
        }else{
            //恢复平衡
        }
    }
}

接下来首先要实现的就是：如何判断一个节点是不是平衡节点？

那肯定是看一下这个node的平衡因子是多少，是不是绝对值在1之内的。

与此同时，平衡因子是通过子节点的高度差计算的，因此需要在节点类里面维护一个高度height属性。

在二叉搜索树的类里节点类添加一个height属性？这是不合适的，因为一个普通的二叉树没必要存在一个height属性。

我们的做法是在AVLTree类中声明一个新的节点类AVLNode，继承普通的二叉搜索树类，然后在AVLNode类中添加height的属性，就可以做的AVLNode类拥有普通二叉搜索树的属性的同时还拥有自己的高度属性。（至于为什么super，这是java语法问题，因为Node父类中没有无参的构造函数，因此子类必须声明构造函数）

public static class AVLNode<Type> extends Node<Type>{
    int height;

    public AVLNode(Type element, Node<Type> parentNode) {
        super(element, parentNode);
    }
}

这样的话，AVL树就有了自己的节点类。但是，我们在外部创建AVL树并添加节点的时候，会调用父类的add方法。然而父类的add方法中创建的节点是普通的二叉搜索树节点Node，而不是AVL树的AVLNode。

所以，我认为，想要使得AVL调用add方法创建的节点类型是AVL本身的且带有height属性的节点，就必须在父类中再提供一个接口给子类使用，默认使用普通二叉搜索树时，创建就是普通的节点，如下所示：

/**
 * 封装创建节点函数
 * @param element 传入的元素值
 * @param parent 传入的父节点
 * @return 返回一个新创建的节点
 */
protected Node<Type> createNode(Type element, Node<Type> parent){
    return new Node<>(element,parent);
}

这样的话，我就在add中把创建节点的地方全换成封装好的函数

/**
 * 添加元素到二叉搜索树中
 * @param element
 */
public void add(Type element){
    elementNotNullCheck(element);//判断添加的节点的元素值是否为null

    //如果添加的是根节点，意味着此时二叉树是空的
    if(rootNode == null){
        rootNode = createNode(element,null);//根节点的父节点就是null，因为没有父节点
        size++;

        //添加节点之后干的事
        afterAdd(rootNode);

        return;
    }

    //程序能到这，说明二叉树已经存在根节点了，那我们添加的就是普通节点了
    /**
     * 添加节点的步骤：
     * 1、找到该节点的插入位置，也就是找到父节点（这一步是核心步骤）
     * 2、创建该节点
     * 3、判断比父节点大还是比父节点小，从而判断是左子节点还是右子节点
     * 如果遇到值相等的元素，那就覆盖掉原有节点
     */

    //任何节点都是从父节点开始找的，所以首先赋值父节点
    Node<Type> currentNode = rootNode;
    //循环的目的是找到插入节点的父节点，因此需要在循环结束的前一刻拿到父节点，初始默认根节点就是父节点
    Node<Type> parent = rootNode;
    //循环的目的不仅要找到插入节点的父节点，还要知道插在左边还是插在右边，因此方向也要记录,所以把决定方向的变量放在循环外面
    int cmp_result = 0;

    while (currentNode != null){
        //当前节点不为空，才可以继续比较；如果在不断地比较之后，当前节点currentNode等于null，说明不能继续比了，此时就要把传进来的节点插入了
        cmp_result = compareNode(element, currentNode.element);
        parent = currentNode;
        if(cmp_result > 0){
            //说明传进来的element大于当前节点的element，那就得向右子树进行搜索，然后继续比较
            currentNode = currentNode.rightChildNode;

        } else if(cmp_result < 0){
            //说明传进来的element小于当前节点的element，那就得向左子树进行搜索，然后继续比较
            currentNode = currentNode.leftChildNode;

        }else {
            // 说明当前节点的element和传进来的element相等，那就覆盖当前值
            currentNode.element = element;
            return;
        }
    }

    //循环完毕，currentNode一定为空，所以要提前保存插入节点的父节点，还要提取保存插入方向
    //创建该节点，把传进来的element赋值给该节点，因为循环结束就知道父节点是谁了，因此这里直接传入
    Node<Type> newNode = createNode(element,parent);
    //判断比父节点大还是比父节点小，从而判断是左子节点还是右子节点
    if(cmp_result > 0){
        //说明该插向右边
        parent.rightChildNode = newNode;
    }else {
        //说明该插向左边
        parent.leftChildNode = newNode;
    }

    size++;//插入完毕后，size要+1

    //添加节点之后干的事
    afterAdd(newNode);

}

这样调整完，原本的二叉搜索树add功能跟之前完全一样，只不过就是封装了一个函数而已。

但是，接下来，就是简直奇迹的时刻：我在AVLTree类中重写了父类的createNode函数，也就意味着，当AVLTree对象调用add函数时，内部调用的createNode函数，就是下方的函数。就做到了，AVL树对象新建节点即区分普通二叉搜索树，又不影响普通二叉搜索树。这就是多态，这就是设计模式，这个就叫做专业（这里为红黑树也埋下了伏笔，将来红黑树也实现这个方法，然后返回自己的节点）。

@Override
protected Node<Type> createNode(Type element, Node<Type> parent) {
    return new AVLNode<>(element,parent);
}

为什么要这样干啊？因为如果不这样干，将来AVLTree对象创建节点就没有height属性，自然也就无法计算平衡因子，从而无法实现恢复平衡的操作。

这样干完之后，我们就可以在AVLNode类内声明一个方法int balanceFactor()，用来返回当前节点的平衡因子。

public static class AVLNode<Type> extends Node<Type>{
    int height;

    public AVLNode(Type element, Node<Type> parentNode) {
        super(element, parentNode);
    }

    /**
     * 获取本节点的平衡因子值
     * @return
     */
    public int balanceFactor(){
        //左子树高度减去右子树高度
        int leftHeight = leftChildNode == null ? 0 : ((AVLNode<Type>) leftChildNode).height;
        int rightHeight = rightChildNode == null ? 0 : ((AVLNode<Type>) rightChildNode).height;
        return leftHeight - rightHeight;
    }
}

这里的技术细节：如果左子树为空，那该节点的左子树高度就为0，否则就为左子树的高度。为什么后面的leftChildNode需要强转，因为普通的leftChildNode是没有height属性的，所以需要强转。

有了可以获取节点平衡因子的方法，那我们就可以判断该节点是不是平衡的了。这里我们在AVLTree类里写一个私有的方法，用来判断传入节点是否平衡：

/**
 * 传入一个Node节点，判断是否是平衡的
 * @param node 普通二叉搜索树的节点，因为调用处是Node类型的，而不是AVLNode类型，调用balanceFactor前需要强转
 * @return 如果小于等于1，返回true，否则返回false
 */
private boolean isBalanced(Node<Type> node){
    return Math.abs(((AVLNode<Type>)node).balanceFactor()) <= 1;
}

封装好这个函数后，我们就可以写在我们最开始搭好的框架里：

@Override
protected void afterAdd(BinarySearchTree.Node<Type> node) {
    while ((node = node.parentNode) != null){
        if(isBalanced(node)){
            //如果node是平衡的
            
        }else{
            //如果node是不平衡的
            
        }
    }
}

我们想要判断节点是否平衡，就必须拿到平衡因子，想要计算平衡因子，就必须拿到左右子树的高度。左右子树的高度默认都是0，因为AVLNode类中并没有对height的任何赋值。这样一来，就会出现这样一个情况：调用isBalanced(node)时，所有节点的高度差都是0 - 0 = 0，所有节点都是平衡的。这样判断来判断去，都是平衡的，显然这是错误的。

因此，我们必须更新节点的高度，我们在AVLNode类里面声明一个方法，用来更新当前节点高度

public static class AVLNode<Type> extends Node<Type>{
    int height = 1;

    public AVLNode(Type element, Node<Type> parentNode) {
        super(element, parentNode);
    }

    /**
     * 获取本节点的平衡因子值
     * @return
     */
    public int balanceFactor(){
        //左子树高度减去右子树高度
        int leftHeight = leftChildNode == null ? 0 : ((AVLNode<Type>) leftChildNode).height;
        int rightHeight = rightChildNode == null ? 0 : ((AVLNode<Type>) rightChildNode).height;
        return leftHeight - rightHeight;
    }

    /**
     * 更新节点高度，即为节点的height重新赋值
     * @return
     */
    public void updateHeight(){
        int leftHeight = leftChildNode == null ? 0 : ((AVLNode<Type>) leftChildNode).height;
        int rightHeight = rightChildNode == null ? 0 : ((AVLNode<Type>) rightChildNode).height;
        height =  1 + Math.max(leftHeight, rightHeight);
    }
}

细心人人可以发现，我们为height的初始值设置为1，因为新添加的节点，一定是叶子节点，因此height一定为1。

紧接着，我们在框架中，这么设计：

@Override
protected void afterAdd(BinarySearchTree.Node<Type> node) {
    while ((node = node.parentNode) != null){
        if(isBalanced(node)){
            //如果node是平衡的,更新当前node的高度，用于下一个node的判断
            ((AVLNode<Type>)node).updateHeight(); 
        }else{
            //如果node是不平衡的，那就恢复平衡

        }
    }
}

细心的人可能会有疑问：程序执行到if(isBalanced(node))，说明node已经变成了新插入节点的parent，我们并不知道parent的左右子树情况，怎么更新这个parent的高度呢？

答案：首先，插入之前，各个节点都是平衡的。因此parent要么只有一个子节点，要么没有子节点。

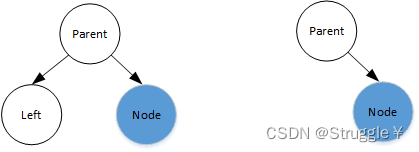
因此，这句代码int leftHeight = leftChildNode == null ? 0 : ((AVLNode) leftChildNode).height;完全可以更新新插入节点的parent的高度。一旦新插入节点的parent被更新了，一路向上，都可以被更新（前提是都是平衡节点）

做一个小小的改动，把更新高度封装一下，把强制转换的代码书写封装成updateHeight(Node< Type> node)，使得更加工整。到时候，我传入节点node，就更新node的高度，很清晰。

private void updateHeight(Node<Type> node){
    ((AVLNode<Type>)node).updateHeight();
}

@Override
protected void afterAdd(BinarySearchTree.Node<Type> node) {
    while ((node = node.parentNode) != null){
        if(isBalanced(node)){
            //如果node是平衡的,更新当前node的高度，用于下一个node的判断
            updateHeight(node);
        }else{
            //如果node是不平衡的，那就恢复平衡

        }
    }
}

现在我们的框架就很清晰了：根据新插入的节点，不断地找parent，看看是否是平衡节点，如果是平衡节点就更新高度（这是必须的，因为不更新高度，就没法计算parent.parent的平衡因子是多少）；如果不是平衡节点，那说明遇到了第一个失衡节点，那就恢复该节点作为根节点的子树平衡。恢复完之后，继续向上找，直到parent==null，就找完了。（实际上，恢复首次失衡节点之后，后面的失衡节点都会恢复平衡的，因此恢复平衡的操作实际上在while循环中只执行了一次）

如下所示，我们会实现一个恢复平衡的函数，一旦执行完毕之后，直接break就完事了。

@Override
protected void afterAdd(BinarySearchTree.Node<Type> node) {
    while ((node = node.parentNode) != null){
        if(isBalanced(node)){
            //如果node是平衡的,更新当前node的高度，用于下一个node的判断
            updateHeight(node);
        }else{
            //如果node是不平衡的，那就恢复平衡
            rebalance(node);
            break;
        }
    }
}

那么现在最最最最关键的，就是如何根据找到的失衡节点恢复平衡！即如何实现rebalance函数呢

如下图所示，是失衡的所有情况。首次失衡的节点，其实就是图中的g点。也就是rebalance的传入的参数。

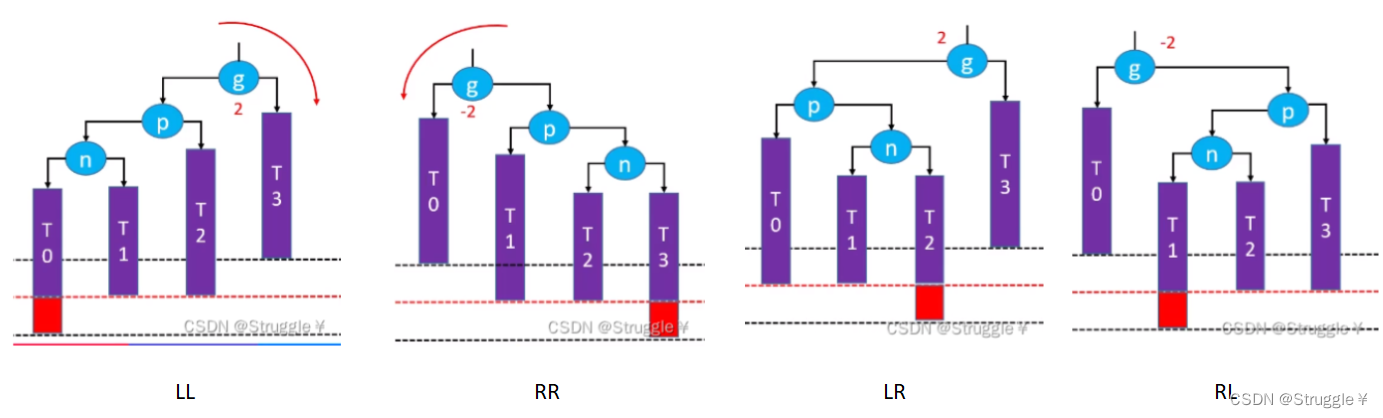现在比较关键的一个问题是，怎么知道失衡的时候，是图中哪一种情况，因为不同的情况，应对的策略是不同的。（时刻牢记rebalance函数传入的节点，一定是g点）为了跟图片对应，我们把rebalance函数的参数写为grand。

/**
 * 恢复以失衡节点作为根节点的子树平衡
 * @param grand 传进来的失衡节点
 */
private void rebalance(Node<Type> grand){

}

我们想要判断，是LL还是RR还是LR还是RL结构，直接的方法就是判断g，p，n三个节点的关系。因为g就是入口参数，所以我们必须想方设法拿到p和n节点。p和n节点是啥呢？怎么拿到呢？

看图可知，p节点是g节点的左右子树高度最高的子节点。n节点又是p节点的左右子树高度最高的子节点。因此，可以通过这个思路根据g点，找到p和n点。

/**
 * 恢复以失衡节点作为根节点的子树平衡
 * @param grand 传进来的失衡节点
 */
private void rebalance(Node<Type> grand){
    Node<Type> parent = grand.tallerChild();
    Node<Type> node = parent.tallerChild();
}

现在我们需要实现tallerChild()成员函数，来获取某节点的最高子节点。如下实现，我们拿到当前节点的左子树的高度和右子树的高度，然后判断谁最高，谁最高就返回谁。当左右子树相等的时候，其实返回左右子树谁都可以。这里我们规定：如果该节点是父节点的左子节点，那么就返回该节点的左子节点，反之亦然。

public Node<Type> tallerChild(){
      int leftHeight = leftChildNode == null ? 0 : ((AVLNode<Type>) leftChildNode).height;
      int rightHeight = rightChildNode == null ? 0 : ((AVLNode<Type>) rightChildNode).height;
      if(leftHeight > rightHeight) return leftChildNode;
      if(leftHeight < rightHeight) return rightChildNode;
      return isLeftChild() ? leftChildNode : rightChildNode;
  }

判断节点是父节点的左子节点还是右子节点，我们写一个方法在父类的Node类中，因为后续可能会用的。

static class Node<Type>{
   Type element;
   Node<Type> leftChildNode;
   Node<Type> rightChildNode;
   Node<Type> parentNode;

   public Node(Type element, Node<Type> parentNode) {
       this.element = element;
       this.parentNode = parentNode;
   }

   public boolean isLeftChild(){
       return parentNode != null && this == parentNode.leftChildNode;
   }

   public boolean isRightChild(){
       return parentNode != null && this == parentNode.rightChildNode;
   }
}

具体的实现就是：父节点不为空且该节点是父节点的左子节点，那isLeftChild()就返回true。这样就可以判断该节点是父节点的左子节点还是右子节点了。

接下来，重点来了！！我怎么判断是LL、LR、RR、RL中的哪一个呢？

因为在前面我们已经拿到了g、p、n三个节点。三个关键的节点在手，判断是哪种结构简直是易如反掌。我们只需要判断p和n是什么类型的子节点，就可以判断是哪种情况。如下所示：当p是g的1左子节点同时n是p的左子节点，那就是LL的情况，以此类推，就可以区分开四种情况：

/**
 * 恢复以失衡节点作为根节点的子树平衡
 * @param grand 传进来的失衡节点
 */
private void rebalance(Node<Type> grand){
    Node<Type> parent = ((AVLNode<Type>)grand).tallerChild();
    Node<Type> node = ((AVLNode<Type>)parent).tallerChild();

	//判断是哪种结构
    if(parent.isLeftChild()){//L
        if(node.isLeftChild()){
            //LL
            
        }else {
            //LR
            
        }
        
    }else {//R
        if(node.isLeftChild()){
            //RL
            
        }else  {
            //RR
            
        }
        
    }

}

只需要对应的情况实现对应的操作就行了。

根据前面的讲解，貌似只需要实现某些节点的旋转操作。左旋转和右旋转对于任何节点来说都是一样的。因此，这里定义两个私有的方法，分别实现节点的左旋转和右旋转。

我画了两个图分别表示左旋转和右旋转的过程。

• grand左旋转，发生节点关系变换的只有grand、parent、parent.left（也可以理解为grand往parent的左子节点上靠）

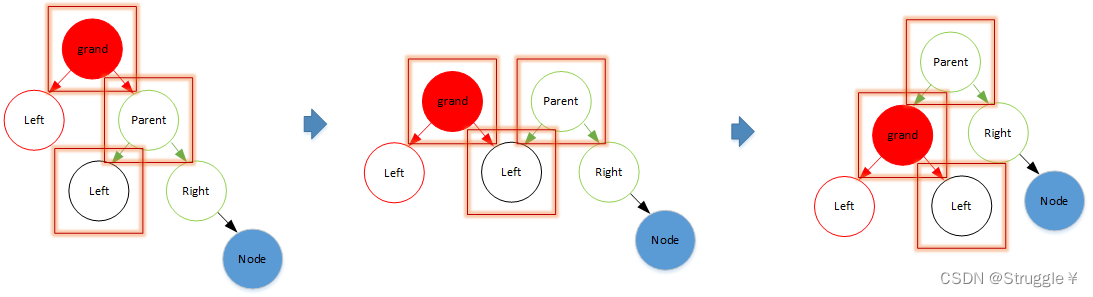
• grand右旋转，发生节点关系变换的只有grand、parent、parent.right（也可以理解为grand往parent的右子节点上靠）

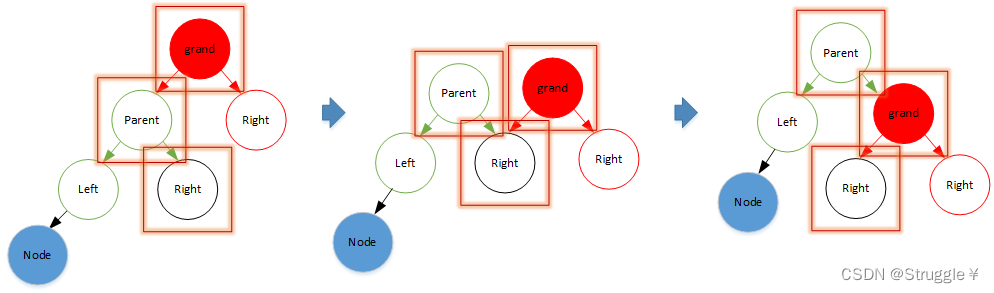
因此，左右旋转的函数内部，只需要处理这三个节点即可。

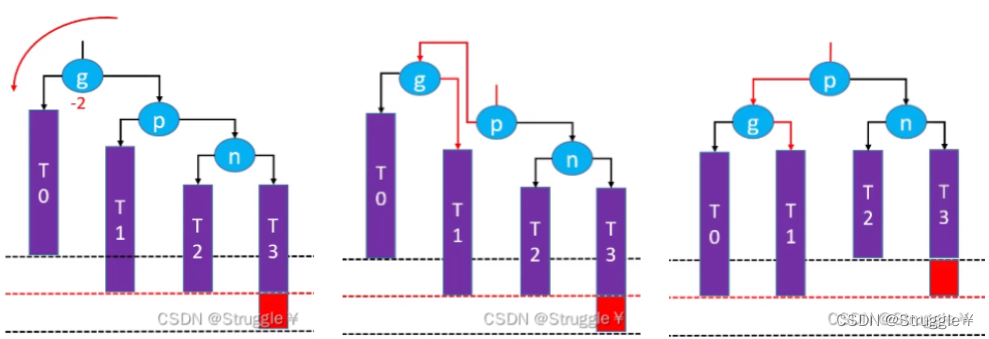
• 我们首先实现节点的左旋转。以RR为例，实现g的左旋转：步骤就是先旋转，然后让p成为这棵树的根节点，然后更新T1和g的parent属性，最后更新g和p的高度（先更新矮的节点，再更新高的节点）。实现代码如下：

private void rotateLeft(Node<Type> grand){

    Node<Type> parent = grand.rightChildNode;
    Node<Type> T1 = parent.leftChildNode;

    //旋转，
    grand.rightChildNode = T1;
    parent.leftChildNode = grand;

    //更新parent的parent属性，让其成为这棵树的根节点
    //成为根节点需要两个条件，第一个是parent的parentNode是原本的根节点的父节点，第二个是原本根节点的父节点需要认定parent是左子节点还是右子节点
    parent.parentNode = grand.parentNode;
    if(grand.isLeftChild()){
        grand.parentNode.leftChildNode = parent;
    }else if(grand.isRightChild()) {
        grand.parentNode.rightChildNode = parent;
    }else {
        //能来到这里，说明node就没有父节点，说明node原本是整棵树的根节点，而现在要让child成为整棵树的根节点
        rootNode = parent;
    }

    //更新T1的parent属性，因为图中的T0~T3都有可能是空的
    if(T1.leftChildNode != null){
        T1.parentNode = grand;
    }

    //更新grand的parent属性
    grand.parentNode = parent;

    //更新grand和parent的高度
    updateHeight(grand);
    updateHeight(parent);

}

有人会问了，为什么更新parent节点的parent属性，需要父节点的左右指向，到了T1和grand就不需要了呢？

问出这种问题，简直是愚蠢，比如我。看看旋转操作干了什么，不就是干了左右子节点指向的问题吗！

//旋转，
grand.rightChildNode = T1;
parent.leftChildNode = grand;

所以在维护节点的parent属性的时候，仅仅给节点的parent赋值是不够的，还需要告诉二叉搜索树，节点是parent的左子节点还是右子节点。

• 现在实现节点的右旋转操作，与左旋转类似。我们以LL为例，实现g节点的左旋转。

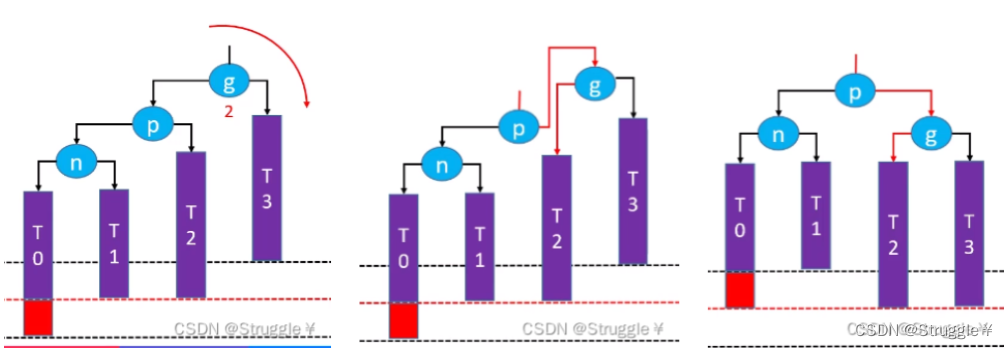
private void rotateRight(Node<Type> grand){

    Node<Type> parent = grand.leftChildNode;
    Node<Type> T2 = parent.rightChildNode;

    //旋转
    grand.leftChildNode = T2;
    parent.rightChildNode = grand;

    //更新p的parent属性，并让其成为这棵子树的根节点
    parent.parentNode = grand.parentNode;
    if(grand.isLeftChild()){
        grand.parentNode.leftChildNode = parent;
    }else if (grand.isLeftChild()){
        grand.parentNode.rightChildNode = parent;
    }else  {
        rootNode = parent;
    }

    //更新T2的parent属性
    if(T2.parentNode != null){
        T2.parentNode = grand;
    }

    //更新g的parent属性
    grand.parentNode = parent;

    //更新g和p的高度
    updateHeight(grand);
    updateHeight(parent);
    
}

左右旋转操作都实现完了，那我们直接根据四种情况，进行不同节点的操作即可

• 对于LL，只需要对g节点进行右旋转
• 对于RR，只需要对g节点进行左旋转即可
• 对于LR，需要先对p节点进行左旋转，然后再对g节点进行右旋转
• 对于RL，需要先对p节点进行右旋转，然后再对g节点进行左旋转

/**
 * 恢复以失衡节点作为根节点的子树平衡
 * @param grand 传进来的失衡节点
 */
private void rebalance(Node<Type> grand){
    Node<Type> parent = ((AVLNode<Type>)grand).tallerChild();
    Node<Type> node = ((AVLNode<Type>)parent).tallerChild();

    if(parent.isLeftChild()){
        if(node.isLeftChild()){
            //LL
            rotateRight(grand);
        }else {
            //LR
            rotateLeft(parent);
            rotateRight(grand);
        }

    }else {
        if(node.isLeftChild()){
            //RL
            rotateRight(parent);
            rotateLeft(grand);
        }else  {
            //RR
            rotateLeft(grand);
        }

    }

}

完美，手撕AVL树！！！！！！！！！！！！！！！！！！（一定要多看，多感受，死记硬背不可取）

打印器的代码（网址），printer里的所有代码复制到同一个包下。

然后二叉搜索树，实现printer的BinaryTreeInfo类的四个接口。string表示向打印节点的什么东西

public class BinarySearchTree<Type> implements BinaryTreeInfo {

@Override
public Object root() {
    return rootNode;
}

@Override
public Object left(Object node) {
    return ((Node<Type>) node).leftChildNode;
}

@Override
public Object right(Object node) {
    return ((Node<Type>) node).rightChildNode;
}

@Override
public Object string(Object node) {
    return ((Node<Type>) node).element;
}

下面我们来测试一下，AVL树的情况：

• 首先是普通的二叉搜索树插入随机的节点

public static void main(String[] args) {

    Integer data[] = new Integer[]{
            85,19,69,3,7,99
    };

    BinarySearchTree<Integer> bst = new BinarySearchTree<>();
    for (int i = 0; i < data.length ; i++) {
        bst.add(data[i]);
    }
    BinaryTrees.println(bst);
}

可以看到，很不平衡。

• 用AVL插入节点试试，可以看到自动修复，实现了AVL树的构建

public static void main(String[] args) {

    Integer data[] = new Integer[]{
            85,19,69,3,7,99
    };

    AVLTree<Integer> avl = new AVLTree<>();
    for (int i = 0; i < data.length ; i++) {
        avl.add(data[i]);
    }

    BinaryTrees.println(avl);
}

删除导致的节点失衡

首先给出一个AVL树

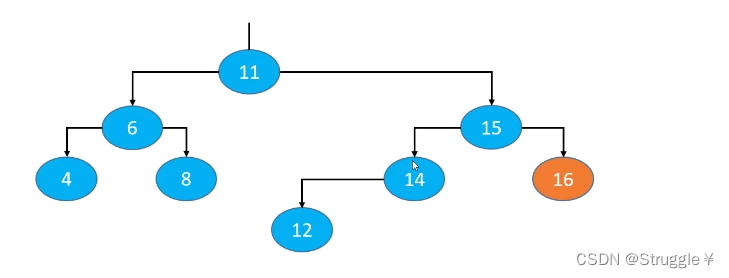
当我删除节点16时，这棵树就不是AVL树了，发现15节点，也就是16原本的父节点失衡了。

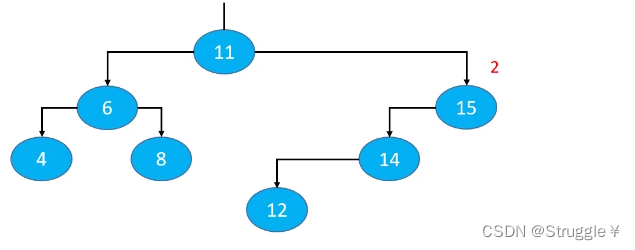
这就是删除可能导致的失衡说明。

删除导致的失衡也是四种情况

删除节点之后，其父节点可能失衡，祖父节点也可能失衡。而且即便父节点恢复平衡之后，祖父节点仍可能失衡。因此，删除导致的失衡不像添加导致的失衡一样，只用恢复一次平衡即可。有可能删除导致的失衡要恢复很多次平衡。

比如下图，我们在旋转完之后，虽然以p为根节点的子树平衡了，但是相对于旋转之前，高度发生了变化，这就可能导致恢复子树平衡的同时，给祖父节点带来了失衡。

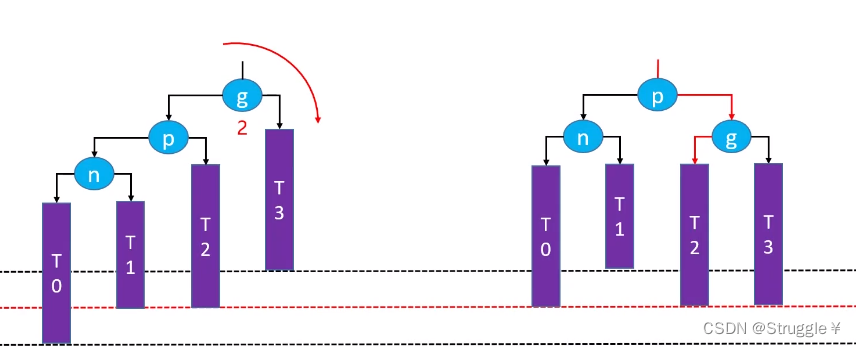
afterRemove和afterAdd仅有一处差别

因此，只需要在afterRemove函数里，把如果不平衡中的break注释掉即可。这样的话，就会一直向上找，知道parent为null。而不是只恢复一次平衡就完事了。

@Override
protected void afterRemove(BinarySearchTree.Node<Type> node) {
    while ((node = node.parentNode) != null){
        if(isBalanced(node)){
            //如果node是平衡的,更新当前node的高度，用于下一个node的判断
            updateHeight(node);
        }else{
            //如果node是不平衡的，那就恢复平衡
            rebalance(node);
            //break;
        }
    }
}

然后在remove函数中，调用多态接口afterRemvoe，实现普通的二叉搜索树啥也不干，AVL树恢复平衡。

/**
 * 私有的，传入节点删除节点
 * @param node
 */
private void remove(Node<Type> node){
    if(node == null) return; //因为element可能不在二叉树中，节点就会返回null，所以这里要判断

    //程序能来到这里，说明节点一定不为空，紧接着就要判断该节点的度，然后采用不同的策略
    size--;

    if(node.leftChildNode==null && node.rightChildNode==null){
        //如果是叶子节点
        if(node.parentNode != null){
            //说明不是根节点,直接删除
            if(node == node.parentNode.leftChildNode){
                //如果是左子节点，就删除左子节点
                node.parentNode.leftChildNode = null;
            }else {
                //如果是右子节点，就删除右子节点
                node.parentNode.rightChildNode = null;
            }

        }else {
            //说明是根节点
            rootNode = null;
        }
        //删除节点之后做的事
        afterRemvoe(node);

    }else if ((node.leftChildNode!=null && node.rightChildNode==null) || (node.leftChildNode==null && node.rightChildNode!=null)){
        //如果是度为1的节点
        if(node.parentNode != null){
            //说明不是根节点,那就父节点指向子节点，就可以把本身删掉
            node.parentNode = node.leftChildNode!=null ? node.leftChildNode : node.rightChildNode;
        }else {
            rootNode = node.leftChildNode!=null ? node.leftChildNode : node.rightChildNode;
        }
        //删除节点之后做的事
        afterRemvoe(node);
    }else {
        //如果是度为2的节点

        //先找到前驱节点
        Node<Type> preNode = predecessor(node);
        //用前驱节点的值覆盖当前度为2的节点的值
        node.element = preNode.element;

        //然后删除前驱节点（前驱节点一定是度为1或者度为0的节点，因为度为2的节点，其左子节点一定是优先前驱）
        if(preNode.leftChildNode==null && preNode.rightChildNode==null){
            //度为0，叶子节点
            if(preNode == preNode.parentNode.rightChildNode){
                preNode.parentNode.rightChildNode = null;
            }else {
                preNode.parentNode.leftChildNode = null;
            }

        }
        if((preNode.leftChildNode!=null && preNode.rightChildNode==null) || (preNode.leftChildNode==null && preNode.rightChildNode!=null)){
            //度为1，可能是只有左子节点，也可能只有右子节点
            preNode.parentNode = preNode.leftChildNode!=null ? preNode.leftChildNode : preNode.rightChildNode;
        }
        //删除节点之后做的事
        afterRemvoe(preNode);
    }
}

因为删除节点要考虑三种情况，因此需在三处，添加afterRemvoe接口。注意，删除叶子节点和度为1的节点，删除的本身就是这两个节点。但是删除度为2的节点，实际上度为2的节点只是元素值被覆盖了，节点并没有删除，真正删除的是前驱节点，因此要在此处调用afterRemvoe(preNode);

测试删除之后能不能恢复平衡

public static void main(String[] args) {

    Integer data[] = new Integer[]{
            85,19,69,3,7,99
    };

    AVLTree<Integer> avl = new AVLTree<>();
    for (int i = 0; i < data.length ; i++) {
        avl.add(data[i]);
    }

    BinaryTrees.println(avl);

    avl.remove(99);

    BinaryTrees.println(avl);

    avl.remove(85);

    BinaryTrees.println(avl);

}

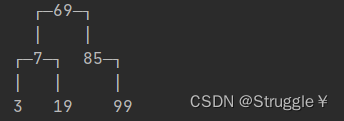
可以看出，试验成功了。删除节点85之后自动恢复了平衡。

AVL树总结

• 添加节点时

可能会导致所有的祖先节点一次性失衡

只要让高度最低的失衡节点恢复平衡，所有的祖先节点会相应的恢复平衡，即整棵树都恢复平衡了

• 删除节点时

刚开始删除时，只可能导致父节点失衡或者祖先节点失衡（只有一个节点失衡），其他节点都不失衡

但是，我们恢复了父节点（或者祖先节点）平衡之后，可能会导致更高层的祖先节点再次失衡，因此我们需要继续遍历祖先节点恢复平衡

• 平均时间复杂度

AVL的搜索节点平均（O(logn)）
AVL的添加节点也是（O(logn)），仅需要O(1)次的恢复平衡操作
AVL的删除节点也是（O(logn)），但是最多需要O(logn)次的恢复平衡操作

对比，普通的二叉搜索树，AVL的效率是大大提高的！！！！这就是AVL树的价值。

B-树（B-Tree）

学习红黑树之前，我们要学习一下B树。因为，B树学不会，红黑树指定学不会。

B树是一种平衡的多路（多叉）搜索树，多用于文件系统，数据库的实现。为什么叫B树呢，有一种说法是Balance Tree，因为B树非常平衡。

下面是B树的一些例子，其中阶数表示这棵B树中有节点存在几阶子节点。比如，三阶B树，表示B树中有节点最多有三个子树，以此类推。

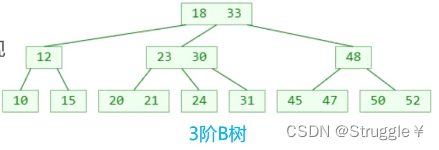
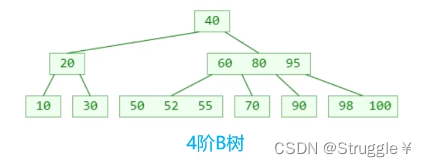
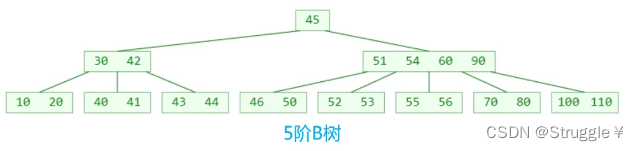
上面三个B树的例子，仔细观察，有什么眼前一亮的特点？

• 一个节点可以存储超过两个元素，一个节点可以拥有超过2个子节点
• 拥有二叉搜索树的性质，比如左子树小于根节点小于右子树
• 非常平衡，每个节点的所有子树高度都是一样的
• 在一定节点数量的情况下，整棵树比较矮

m阶B树的性质（m>=2）

m阶B树对节点内元素的个数，以及节点的子节点个数有着强制的要求。必须满足这些要求，才叫B树。

• 假设一个节点可以存储的元素个数为x个，那么这个x有着明确的范围（不能多也不能少）
  1、如果这个节点是这棵树的根节点，那么根节点可以存储的元素个数为：1 ≤ x ≤ m-1
  2、如果这个节点不是根节点，那么这个节点可以存储的元素个数为：ceiling(m/2)-1 ≤ x ≤ m-1

先解释一下为什么所有的节点个数都不能超过m-1呢，因为m阶B树的定义就是存在某个节点的子节点个数是m个。因此，这个节点个数必须是m-1。所以，总结下来，就是所有的节点内存储的元素个数不能超过m-1，最多是m-1。

再解释一下，为什么根节点内元素的个数大于等于1就行，而非根节点必须大于等于这么一个数ceiling(m/2)-1。这个是为了后续处理上溢下溢巧妙设计的数值（细心地可以发现2*（ceiling(m/2)-1）永远是小于等于m-1的），记住就行了。

• 如果是非叶子节点，必须都要有子节点，而且子节点必须是满的（意味着父节点有x个元素，子节点必须有x+1个）
  1、如果父节点是根节点，那么子节点的个数y必须满足：1+1 ≤ y ≤ m-1+1 --> 2 ≤ y ≤ m
  2、如果父节点是非根节点，那么子节点的个数y必须满足：ceiling(m/2) ≤ y ≤ m

也就是，子节点的个数必须是父节点中元素个数加1，前提是这个父节点是非叶子节点。

比如，m=3时，3阶B树，2 ≤ y ≤ 3，又可以称作：2-3树

m=4时，4阶B树，2 ≤ y ≤ 4，又可以称作：2-3-4树

4阶B树，我们需要重视起来，因为跟后面即将学习的红黑树有着千丝万缕的联系。

B树和普通二叉搜索树的关系

B树和二叉搜索树在逻辑上是等价的。

以下图为例：可以看到根节点存储着两个元素18和33。18的左边指向一个子树，子树中的所有值都是小于18的；18的右边33的左边也指向一棵子树，可以看到这棵子树所有值都是大于18且小于33的。33的右边也指向一棵子树，这棵子树所有值都是大于33的。这本质不就是二叉搜索树嘛！！！

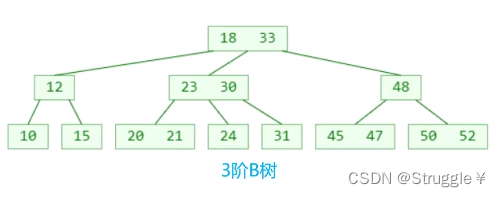
我们给出这棵B树的前世，二叉搜索树，可以看到逻辑完全一致。

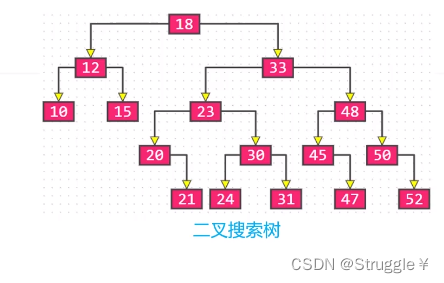
总结：B树就是二叉搜索树的变种。变成了每个节点可以存储多个元素，每个节点又可以有多个子树。这种需求在数据库中是非常有用的，因此B树是有应用场景的。

在B树中搜索元素

跟二叉搜索树类似，具体步骤如下：

1. 现在节点内部从小到大开始搜索元素
2. 如果命中，搜索结束
3. 如果未命中，再去对应的子节点搜索元素，重复步骤1

假如我要找72这个元素，从根节点开始找，发现比40大，向右子树开始找，找到60，发现比72小，继续在此节点中向右找，找到80发现比72大，说明这个节点中没有72，那就要往下一个子节点中找，发现70比72小，继续右子节点找，发现为空，表示没找到。

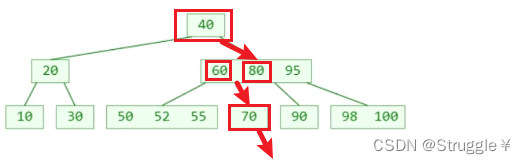
总结，跟二叉树唯一的区别就是，节点里元素不一定是一个，如果是多个，首先在节点里找，看能不能找到，如果找不到，根据值的大小，到相应的子树中找即可。

向B树中添加元素（很复杂）

**新添加的元素必定是添加到叶子节点。**这是B树的性质。为什么呢？想想二叉搜索树的添加，是不是不断地比较然后添加在末端。既然换成了B树，那么新添加的元素，一定是塞到叶子节点中的。

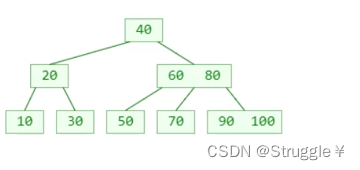
比如，新添加一个55，就塞到了原本装有50的叶子节点中。

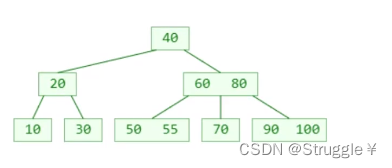
再添加一个95

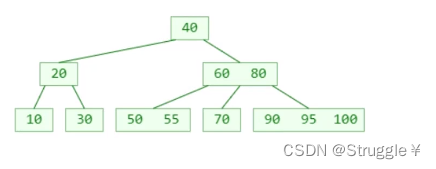
此时我再添加一个98（我要求这是一棵4阶B树，也就意味着所有节点最多只能存储3个元素），也就意味着如果再按照正常流程添加，最右下角的叶子节点的元素个数将超过限制，这种情况我们成为节点出现了上溢（overflow）。这就不是一棵B树了，显然B树不允许这种情况出现，那该怎么调整呢？？？？

解决B树节点的上溢（由添加导致）

我们以5阶B树为例，解释如何解决节点的上溢问题。

假设我们在节点中插入元素36，此时该节点内部就存储了5个元素。这显然违背5阶B树的特点，因为节点存储的元素超过了规定数，这就叫做节点的上溢。

我们说明一些数据：

• 上溢一旦发生，节点的元素个数必然等于m
• 假设上溢节点中间的元素位置是k，那我们做法就是将k位置的元素向上与父节点合并
• 并将【0，k-1】和【k+1，m-1】两个区间的元素分裂成两个子节点，分别作为作为原先k位置元素的左右子节点

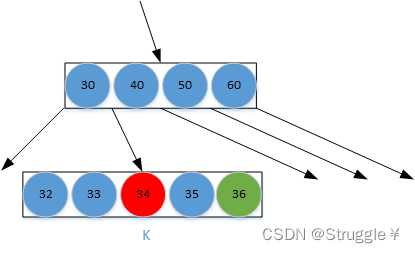
处理完之后就这样：

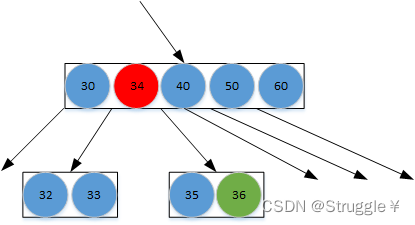
但是，这么处理，可能会导致父节点再次上溢。因为，我们还要继续对上溢的父节点进行相同的处理。直到处理到根节点为止。比如，我们再让上溢节点中的中间节点40与父节点合并，然后把剩余的部分分裂成两个子节点。假如，40所在的节点不上溢，那就到此位置。如果继续上溢，那就继续处理。

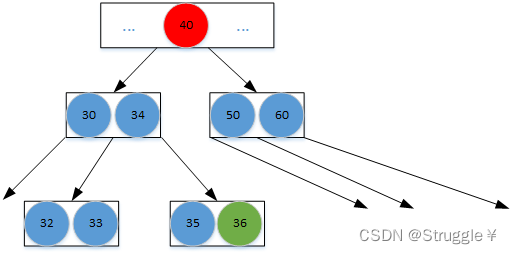
如果上溢到根节点，那就会从原本的根节点中揪出一个元素作为新的单独的根节点。这是唯一可以让B树长高的一种情况：那就是上溢现象蔓延到根节点。

从B树中删除元素

• 假如删除的元素在叶子节点中，那么直接删除即可
  
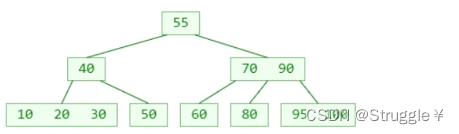
  比如说删除元素30，直接删除即可：
  

• 假如删除的元素不在叶子节点中，那删除起来就很麻烦了
  
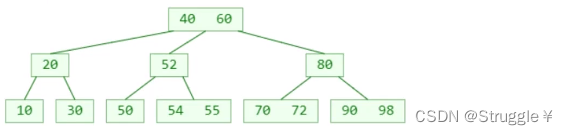
  假如我要删除的60，就没法直接删除。因为60删除完之后，根节点中只有一个元素，但是根节点是有三个子节点的。B树的特点就是元素个数 + 1 = 子节点个数。如果直接删掉，是不符合B树特性的。

那我们怎么办呢？

• 需要找到该元素的前驱元素或者后继元素，然后用其覆盖掉该元素
• 并把前驱元素或者后继元素删除（因为非叶子节点的前驱元素或者后驱元素在B树中一定是存在于叶子节点，叶子节点中的元素直接删是没问题的）
  
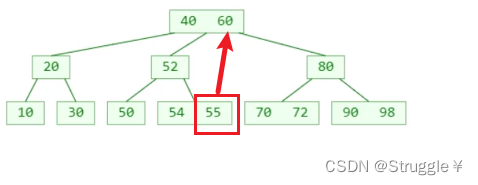
  覆盖并删除，就变成了这样：B树中真正被删除的是叶子节点里的元素。
  

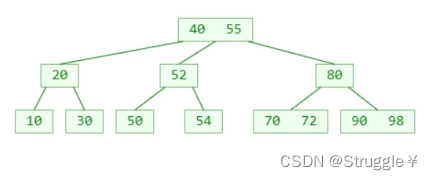
解决B树节点的下溢（由删除导致）

从前面的理论得知，5阶B树除了根节点外，其他节点最少要有2个元素，最多有4个元素（非根节点中元素个数范围：ceiling(m/2)-1 ≤ x ≤ m-1）。下面举例说明：

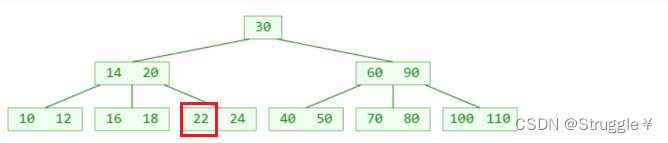
叶子节点被删除掉一个元素后，元素的个数可能会低于最低限制（ceiling(m/2)-1）。

假设我要删除元素22（假设这是一棵5阶B树），那么该节点的元素个数就会变为1个，明显低于2。

发生这种现象，叫作节点的下溢（underflow）。

现在我们来解决下溢的问题。

还是先明确一些条件：

下溢节点的元素数量必然等于ceiling(m/2)-2

如果下溢节点的临界兄弟节点有至少ceiling(m/2)个元素，可以将其借一个元素。

如下图所示：

• 将父节点元素b插入到下溢节点的首位置
• 用兄弟节点的元素a（离下溢节点最近的元素）替代父节点中的元素b
  
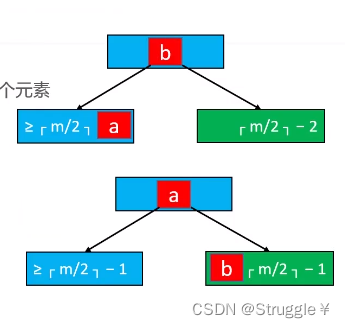
  但是并不是只有这几个操作：a元素一定要左右子节点，其中d节点我省略了没画出来，但是其实还要对d做处理：最终还要把d作为b的左子树。根据B树性质，d一定是大于a小于b的，因此，需要放在b的左子树上。
  

如果下溢节点的临界兄弟节点只有ceiling(m/2)-1个元素，那该怎么办呢？ 比如下方示意图：

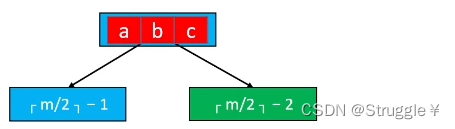
我们要做的事，看好了：将父节点中的元素拿下来，跟左右子节点合并。合并后成为一个节点，元素个数为ceiling(m/2)-1 + 1 + ceiling(m/2)-2 = 2 * ceiling(m/2) - 2。当m为偶数的时候，2 * ceiling(m/2) - 2 = m-2，当m为奇数的时候，2 * ceiling(m/2) - 2 = m-1。无论哪种情况，合并后的节点中元素的个数都没有超过m-1，都满足B树的要求，并不是使得新节点产生上溢。

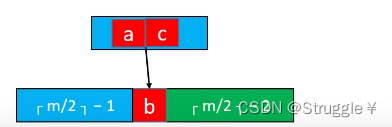
这就是B树的作者在设计B树元素个数规则时，巧妙的地方。

但是，这个操作可能会导致父节点再次下溢，因为父节点少了一个元素啊。我们再次按照相同的逻辑解决父节点的下溢就行了。最坏的情况，这种下溢会一直蔓延到根节点，我们需要逐一解决。

总结：一个节点产生下溢了，先看看有没有兄弟节点有能力借一个元素给他，如果没有就把父节点中拉下来一个，合并即可，如果此时父节点下溢了，继续解决就好了。

如果下溢现象一致传播到根节点，那就可能会使得根节点跟下面的节点合并，这也是唯一一种可以使得B树变矮的可能：下溢现象蔓延到根节点。

4阶B树

4阶B树的性质：

• 无论是根节点还是非根节点，每个节点能存储的元素个数都是[1, 3]
• 那么所有非叶子节点的子节点个数都是[2, 4]

4阶B树有助于红黑树的学习，因此这里单独提及一下其性质。

推荐一个网站，可以可视化这些树的添加和删除过程

进入B树的页面，可以看到如下操作台：

在这里，我们可以观察每一次插入或者删除的过程，更加清晰的理解B树建立的过程。下图为我建立的四阶B树的样子：任意节点最多存在四个子节点，每个节点里的元素个数是1到3。

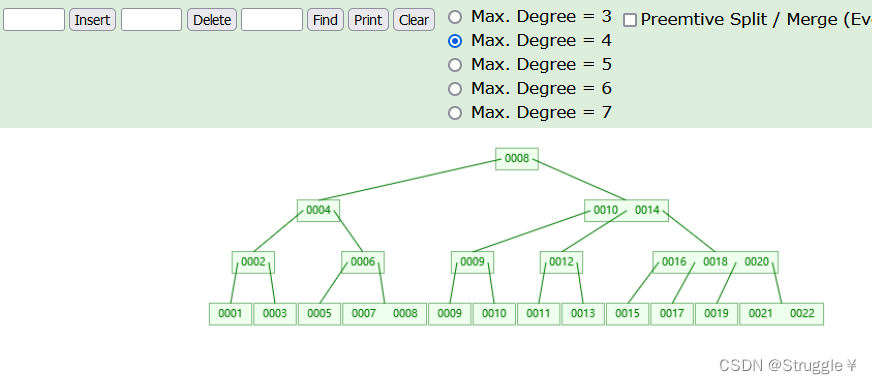
红黑树（Red Black Tree）

红黑树也是一种自平衡的二叉搜索树，听名字就知道，这棵树由红色节点和黑色节点组成。如下所示，就是一棵红黑树。

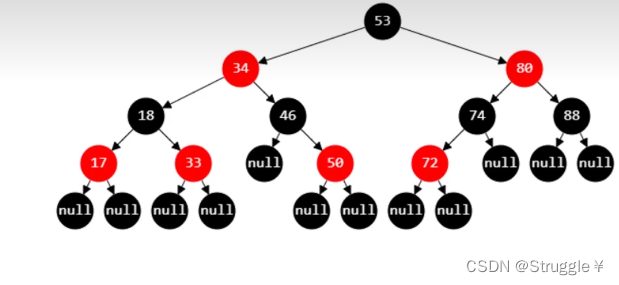
红黑树的五大性质

1. 节点是red和black颜色组成
2. 根节点必须是black
3. 红黑树认定自己是一棵真二叉树，所以会将所有度为1或者度为0的节点，通过添加null的子节点使其成为度为2的节点。这些null节点，是红黑树臆想出来的黑色节点，写代码时不用管。
4. red节点的子节点必须是black节点（推导出的2个结论是：red节点的父节点必须是black；从根节点到叶子节点所有路径上不能由2个连续的red节点）
5. 从任意节点到其叶子节点的所有路径都包含相同数目的black节点

为何在这些规则的约束之下，红黑树就是一棵自平衡二叉搜索树呢？ 这里埋下一个伏笔，等介绍完红黑树的全部性质之后，再解答这个问题。

红黑树与4阶B树的等价变换（非常重要）

下图是一个满足红黑树要求的红黑树。

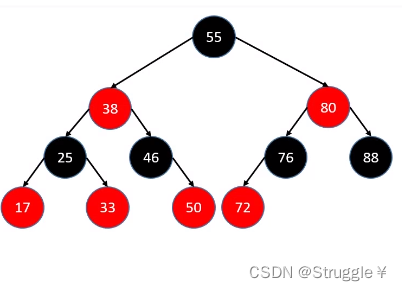
接下来我们根据一个原则，对它进行一点点表达上的改变。这个原则是：红色节点向黑色父节点靠拢，与黑色父节点放在一行摆放。没有红色子节点的黑色节不需要做任何处理。就变成了下面的样子，这棵树仍然保持着二叉搜索树的原则。

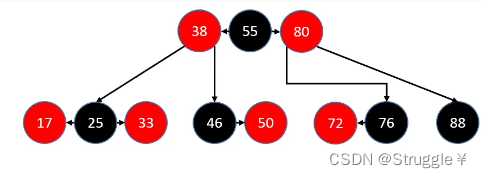
（可以看到，红色子节点自动向黑色父节点靠拢，并放置在同一行。没有红色子节点靠拢的黑色节点，那就独立成为一个节点即可。）

我们把这种形式再转换一下，变成B树的样子：仔细看，是4阶B树。

因此，红黑树和4阶B树在某种程度上完全等价！本质上是红黑树中的黑色节点和其红色子节点融合在一起形成一个独立的B树节点，而且红黑树中的黑色节点个数与4阶B树的节点总个数相等。

为什么红黑树来回融吧融吧就能和4阶B树等价呢？

因为：4阶B树要求节点内元素个数不超过三个不小于1个。红黑树一个黑色节点最多有两个红色子节点。最少一个没有。因此融合在一起最多元素个数就是3个，最少就是一个。而且，因为每个节点最多三个元素，因此子节点最多就是四个。所以，完全可以用4阶B树等价红黑树。

（ps：网上有一些教程拿3阶B树与红黑树进行类比，这是非常不严谨的，3阶B树并不能完全匹配红黑树所有的可能）

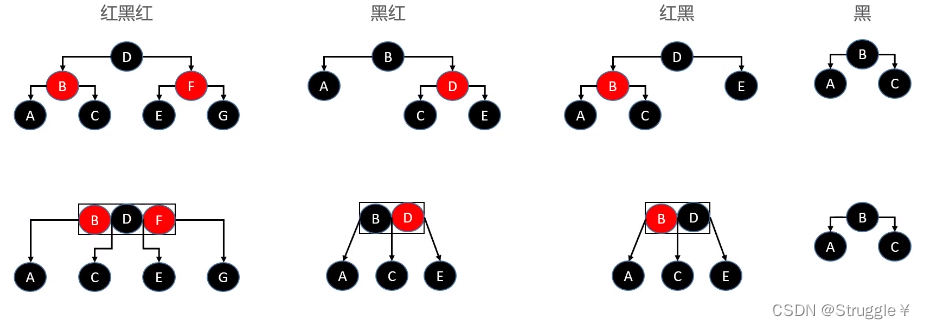
如下图所示，红黑树转换到B树的四种情况：

• 红黑红（左右子节点都是红）组成一个B树节点
• 黑红（红色是右子节点）组成一个B树节点
• 红黑（红色是左子节点）组成一个B树节点
• 黑，自己就可以组成一个B树节点

声明一些辅助函数（有助于我们方便构建红黑树）

先来看几个英文单词：

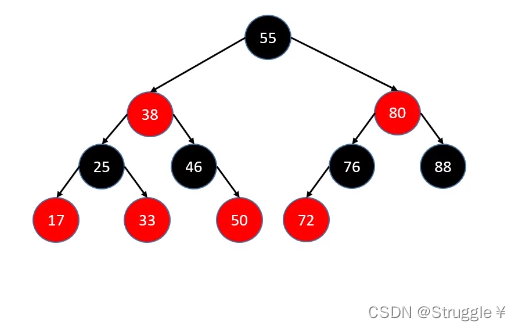
• parent：父节点，这个就没啥好说的了，50的父节点是46
• sibling：兄弟节点，同一个父节点的左右子节点叫做兄弟节点，比如17和33就是sibling
• uncle：叔父节点，父节点的兄弟节点叫做叔父节点，比如50的uncle是25,33的uncle是46
• grand：祖父节点，parent的父节点。比如，50的grand是38

接下来，封装一些辅助函数，为了将来添加删除节点时，做一些操作提供方便。

定义辅助函数之前，我们先定义红黑树的节点类，跟AVL树一样，需要继承普通的二叉搜索树中的通用节点类，并在此基础上，新增一个节点color属性。

private static final boolean RED = true;
private static final boolean BLACK = false;

public static class RBNode<Type> extends Node<Type> {
    boolean color = RED;//要有一个对比于普通二叉搜索树的颜色属性

    public RBNode(Type element, Node<Type> parentNode) {
        super(element, parentNode);
    }
}

这里，我们将color设置为布尔类型，并存储在常量里。

第一个辅助函数，为节点染色。因为红黑树的一个特点就是每个节点都有一个颜色属性，而将来我们在建立红黑树的时候，避免不了为节点染色。

/**
 * 为节点node染色color,并返回染色后的节点
 * @param node
 * @param color
 * @return
 */
private Node<Type> color(Node<Type> node, boolean color){
    if(node == null) return node;
    ((RBNode<Type>)node).color = color;
    return node;
}

下面，基于这个封装函数，设置两个针对性的染色函数：把节点染成红色和把节点染成黑色。

/**
 * 把节点node染成红色，并返回染色后的节点
 * @param node
 * @return
 */
private Node<Type> red(Node<Type> node){
    return color(node,RED);
}

/**
 * 把节点node染成黑色，并返回染色后的节点
 * @param node
 * @return
 */
private Node<Type> black(Node<Type> node){
    return color(node,BLACK);
}

我们一定有这样一个需求：想知道当前节点是什么颜色。因此，我们需要声明一个函数用来返回当前节点的颜色。

/**
 * 判断某个节点是什么颜色
 * @param node
 * @return
 */
private boolean colorOf(Node<Type> node){
    //如果是空的，那就返回黑色，否则返回对应的颜色就行
    return node == null ? BLACK : ((RBNode<Type>)node).color;
}

紧接着，就可以设定两个针对性的返回节点颜色的函数：判断节点是不是黑色和判断是不是红色。

/**
 * 判断节点node是不是黑色
 * @param node
 * @return
 */
private boolean isBlack(Node<Type> node){
    return colorOf(node) == BLACK;
}

/**
 * 判断节点node是不是红色
 * @param node
 * @return
 */
private boolean isRed(Node<Type> node){
    return colorOf(node) == RED;
}

还有，我们在前面介绍了兄弟节点和叔父节点。因此，我们也要提供接口，返回这两个节点。

我们在二叉搜索树类中的Node类中声明这个接口，因为，只要是二叉搜索树都可以有这个性质。

public Node<Type> sibling(){
    if(isLeftChild()){
    	//如果该节点是父节点左子节点，那就返回父节点的右子节点
        return parentNode.rightChildNode;
    }
    if(isRightChild()){
    	//如果该节点是父节点右子节点，那就返回父节点的左子节点
        return parentNode.leftChildNode;
    }
    //如果该节点既不是左子节点也不是右子节点，说明没父节点，那就没兄弟节点，直接返回null
    return null;
}

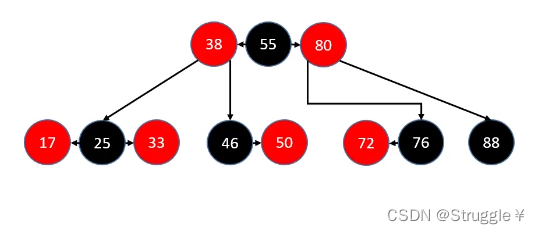
红黑树的添加节点

在向红黑树中添加节点时，一定要做到心中有B树（谐音：心中有b数，哈哈哈）。为了让我们心中有B树，我故意将红黑树展示成B树的样子。

在添加新节点之前，我们需要再次阐明一些已知条件。

• B树中，新元素必定是添加的叶子节点中去的
• 4阶B树的所有节点元素的个数都满足[1, 3]

建议，新添加的节点默认为RED红色，这样的话，能够让红黑树的性质尽快满足。（性质1,2,3,5都满足，性质4不一定）

1. 节点是red和black颜色组成
2. 根节点必须是black
3. 红黑树认定自己是一棵真二叉树，所以会将所有度为1或者度为0的节点，通过添加null的子节点使其成为度为2的节点。这些null节点，是红黑树臆想出来的黑色节点，写代码时不用管。
4. red节点的子节点必须是black节点（推导出的2个结论是：red节点的父节点必须是black；从根节点到叶子节点所有路径上不能由2个连续的red节点）
5. 从任意节点到其叶子节点的所有路径都包含相同数目的black节点

因为，新插入的节点是红色，万一插入在红色父节点上，就不满足性质4了。（此时就需要调整红黑树的节点，使其再次变成一个红黑树）

如果，我们首次添加，也就是添加的根节点，需要在默认红色的基础上染成黑色。

下面，重头戏来了，添加节点时可能遇到的所有情况（只可能添加到最后一层，那我们就需要知道最后一层有哪些种情况，一一列举，一一解决即可）。

如图所示，我们添加节点只可能添加到最后一层。而且，最后一层可能出现的节点情况只有四种（红黑红，黑红，红黑，黑）

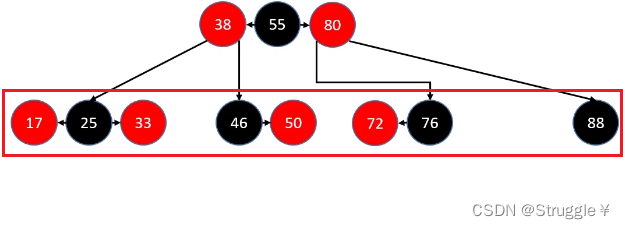
那么，添加新节点总共有多少种情况呢？答案是12种，下图展示了可能的插入情况。

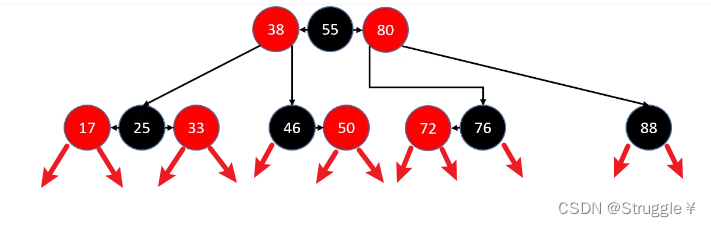
下面，我们分析这些情况下，添加新节点是不是导致了红黑树性质不满足了。如果满足就不用做任何处理，如果不满足那就要恢复红黑树的性质，也就是要在afterAdd函数里搞事情了。

• 有四种情况下，添加节点依然满足红黑树的性质4：红色新节点插在了黑色父节点上，也就是parent的颜色是BLACK。下图展示了这四种情况，可以不用做任何处理，依然满足红黑树的性质（同样也满足B树性质），不需要修复。

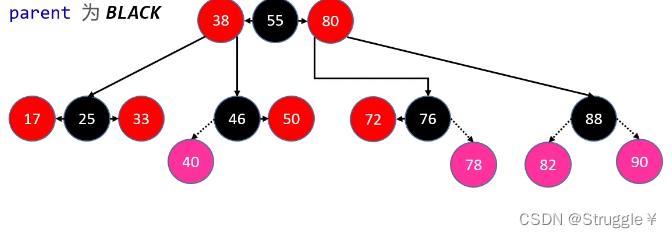
剩下的8种，都是不满足红黑树的性质，需要修复。（那就是新插入的阶段插在了红色父节点上，这样就是两个红节点连着了，是不满足性质的。如下图所示

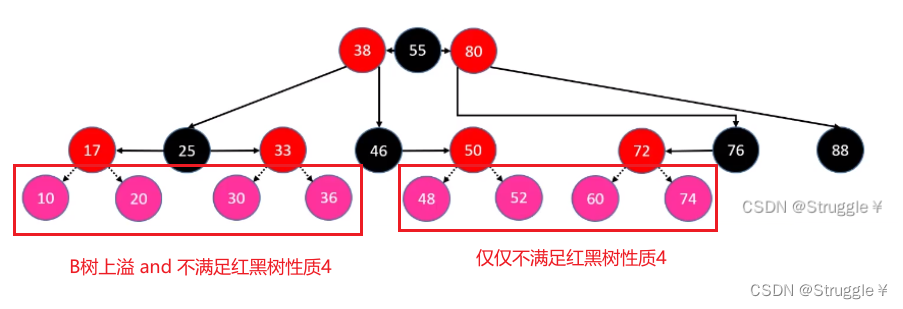
前四种情况，不仅不满足红黑树的性质，还不满足B树的性质。后四种情况，仅仅不满足红黑树的性质。我们首先解决后四种情况。

• 符合LL/RR的情况：就是下图这两种情况
  
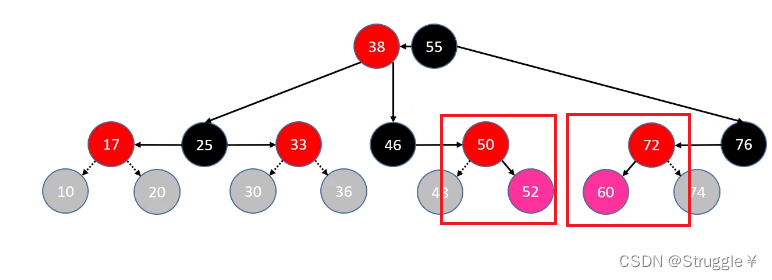
  这种情况下，我们插入的是红色节点，最好的满足性质，就是把原本是红色父节点染成黑色。然后把祖父节点染成红色变成父节点的子节点，最后让祖祖父节点指向父节点。（看明白了吧，对于46节点来说，相当于进行了一次左旋转，对于76节点来说，相当于进行了一次右旋转）

疑问1：为什么要把父节点染成黑色？（因为插入的红色节点，想要满足性质就得把父节点变成黑的）
疑问2：为什么要把祖父节点染成红色？（因为B树中的节点对应于红黑树中，一定是黑色节点是父节点，子节点都是红色节点或者没节点。如果祖父节点是黑色，那说明当前节点不是最后一层叶子节点）
疑问3：为什么要祖父节点指向父节点？（因为父节点以及成为了这个B树节点的黑色父节点，所以祖祖父节点要指向新的父节点）

这两个符合LL、RR的情况，变换后就是下面的样子（可以看出没有破坏二叉搜索树的性质还修复了红黑树的特性）

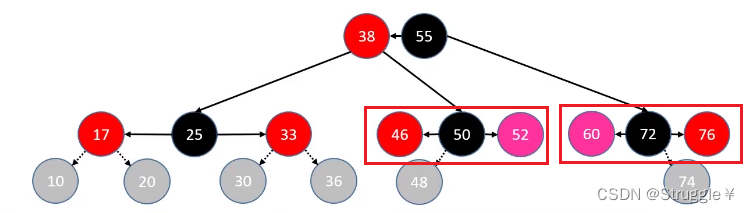
总结判定条件如下：

• 符合LR/RL的情况：就是下图的两种情况
  
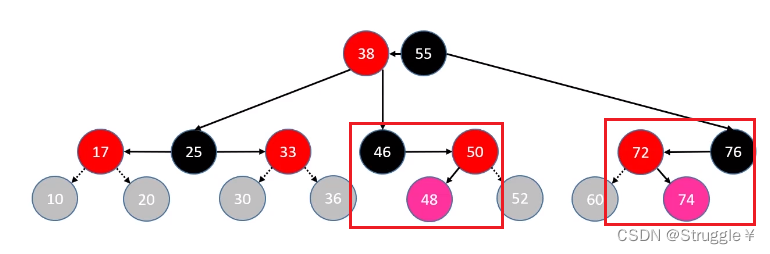
  这种情况让50进行右旋转，然后在对46进行左旋转，然后48就变成了这个B树节点的根节点，所以48指定是要染成黑色的，另外两个就染成红色（第二个同理）
  
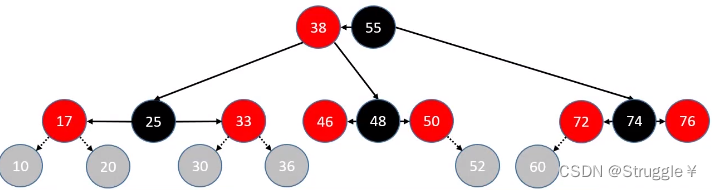
  总结判定条件如下：
  

为啥判定条件，是uncle不是RED呢？因为8种情况的后四种具有一样的特点，所以我们归为一类处理（仅仅造成红黑树性质4不满足），而前四种情况不仅会对红黑树的性质造成破坏，还会对4阶B树性质造成破坏。所以我们将前四种归为一类处理。那想要区分前四种还是后四种，最直接的方法就是判断新插入节点的uncle是不是RED。因为，如果是RED说明就是前四种，如果是黑色（NULL节点）就是后四种。

现在，我们来处理前四种比较麻烦的情况：

• 上溢LL情况：如下所示，插入节点10。同时违背了红黑树和B树的性质。
  
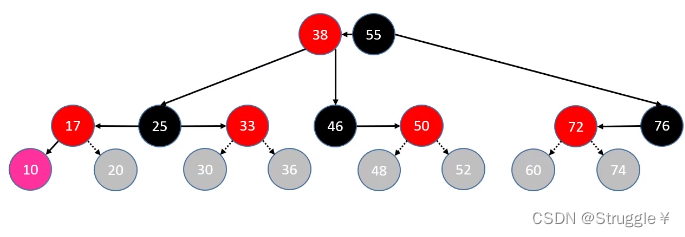
  记不记得，B树中如何处理上溢现象了？总结为8个字就是：向上合并，左右分裂独立成B树节点。也就是说，挑出上溢节点中大概中间的元素向上合并到父节点里，然后上溢节点分裂。B树的处理完了，还要符合红黑树的性质，因此还要染色。

25比较合适向上合并，因为25本来就是38的子节点。对于父节点来说，25就是新插入的节点。因此完全可以递归处理。然后左右分裂成两个独立的B树节点，因此17和33都要染成黑色。

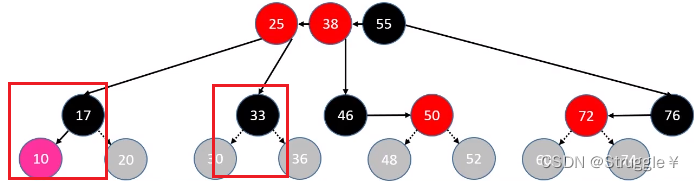
既然把25当做新添加的节点，那我觉得把25染成红色，然后继续调用我们设计的添加修复操作，完成新节点的插入（递归）。总结步骤就是如下：

grand向上合并，然后染成RED并不是适用于所有情况。假如，我们将grand向上合并再次发生上溢呢？这种上溢一直持续到根节点呢？如果发生这种情况，持续到根节点，那就不能把grand染成RED，就必须染成BLACK了。这一点需要注意一下。

• 上溢RR情况：跟LL情况类似，只需要合并、分裂染色即可。然后对合并上去的递归处理
  

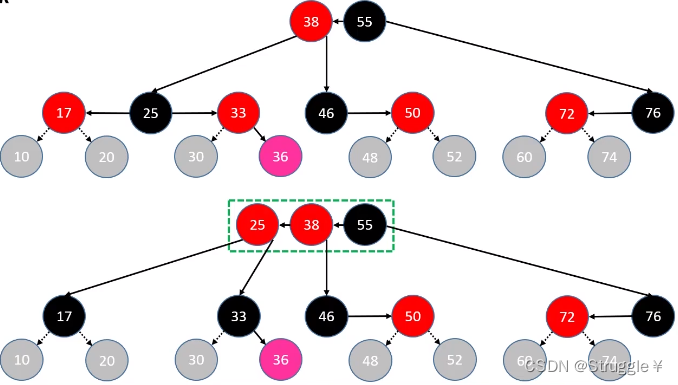
• 上溢LR情况：依然是合并、分裂然后染色。然后对合并上去的递归处理
  

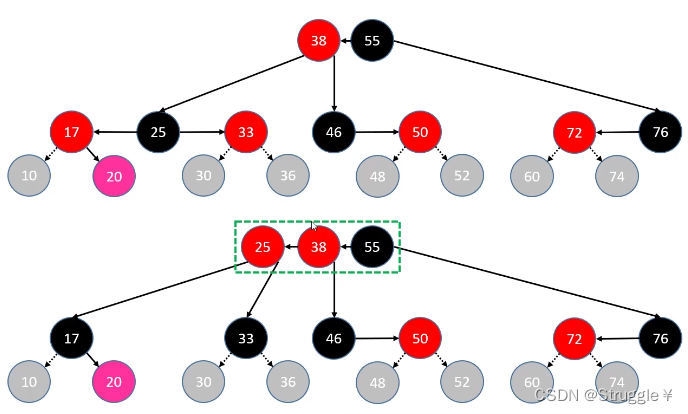
• 上溢RL情况：依然是合并、分裂然后染色。然后对合并上去的递归处理
  

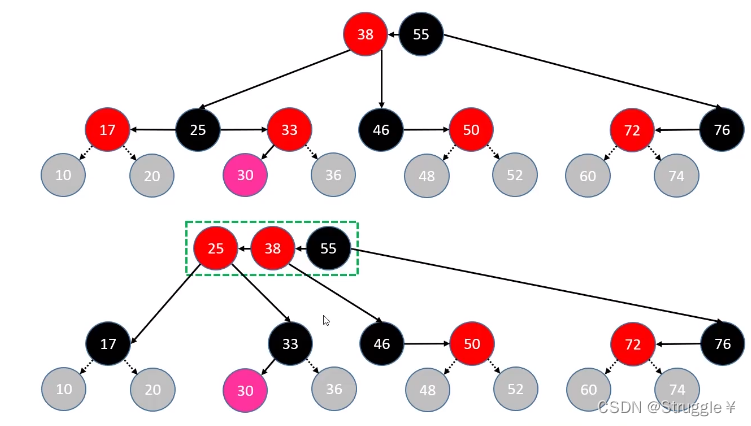
添加节点情况总结：

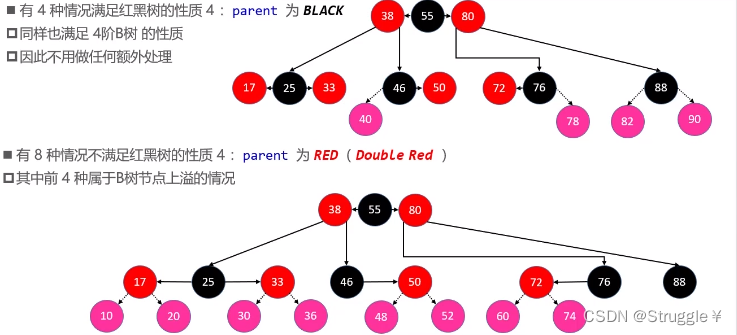
8种情况不满足红黑树的性质4，其中前四种还不满足B树性质。

前四种：无论是LL/RR/RL/LR，仅需要染色，分裂，并且向上合并看做一个新添加的节点即可。都没有旋转操作

• LL：
  

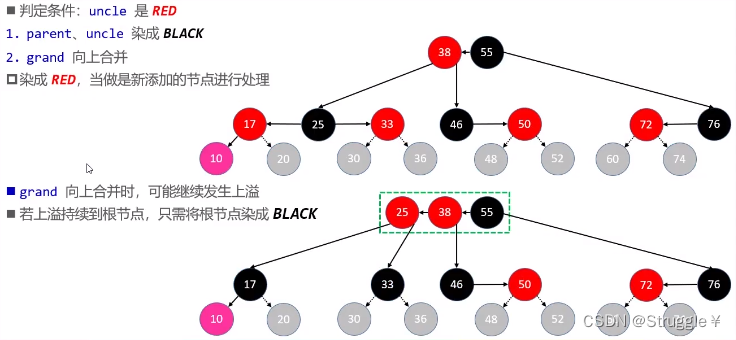
• RR：
  

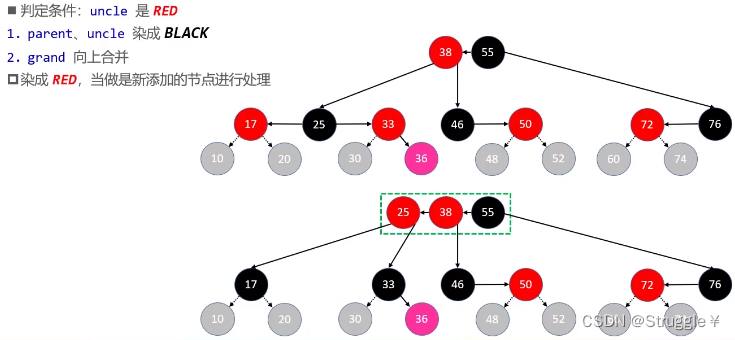
• RL
  

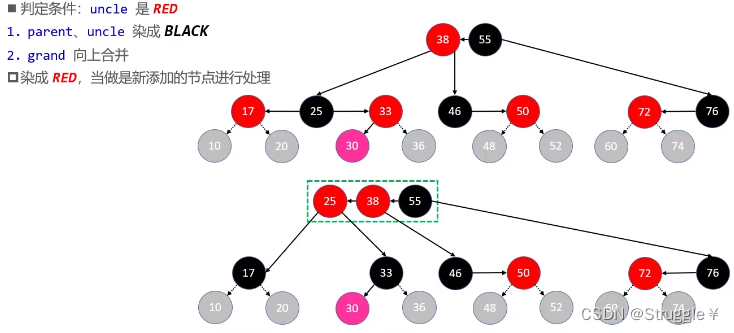
• LR
  

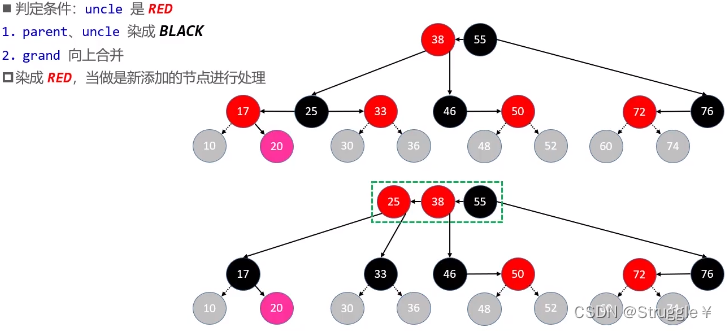
后四种情况：LL/RR需要单旋加染色，LR/RL需要双旋加染色。

LL/RR：需要单旋转+染色

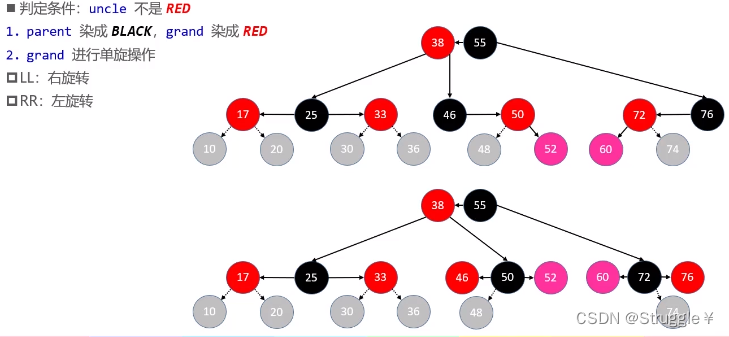
RL/LR：需要进行双旋转+染色

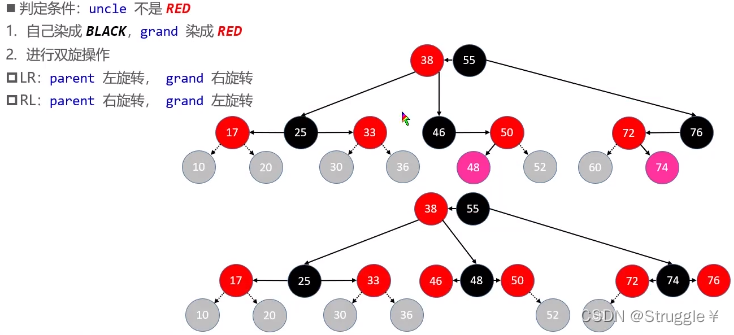
红黑树删除节点

首先，回忆一个非常重要的定理：在B树中，真正发生内存删除的元素，都在叶子节点中。

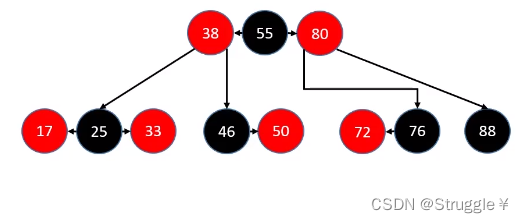
如果删除的是红色节点，不用作任何调整

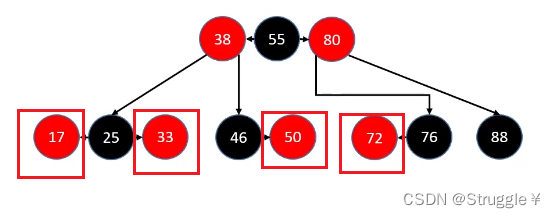
最棘手的就是删除黑色节点。删除黑色节点，分为三种情况：

• 拥有两个RED子节点的BLACK节点：比如图中的25，不可能直接删除25，指定是找到前驱或者后继替代，本质上删除的还是红色的字节点17或者33，因此这种情况不用考虑
  
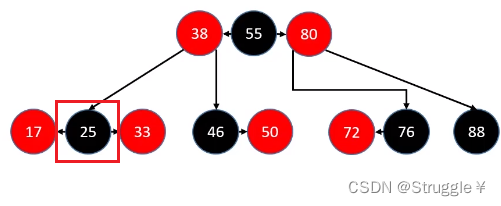
• 拥有一个RED子节点的BLACK节点，也就是图中的46或者76
  
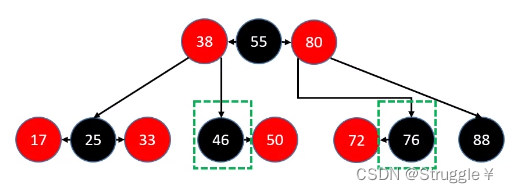
• 最后一种情况，删除的是BLACK叶子节点，就是图中的88

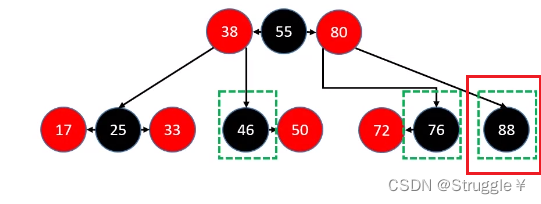
所以，我们需要处理的就三种：拥有一个RED子节点的BLACK（可能是左子节点也可能是右子节点），BLACK叶子节点。

首先，我们来看看像46和76这样的节点，如何删除（46和76这样的节点叫做拥有一个RED子节点的BLACK节点）。如何判断是不是这种节点呢？

判定条件为：用以替代的子节点是RED，反之就是88这种节点。

具体做法就是：把想要删除节点删除，然后替代你的染黑即可。也就是把50和72染黑，然后被之前的父节点指向。

这很简单！

现在到了最最最难，最最最繁琐，也是判断条件最多的情况下了：那就是删除的是，单独的，黑色叶子节点！！！

也就是，删除的是88这种节点。

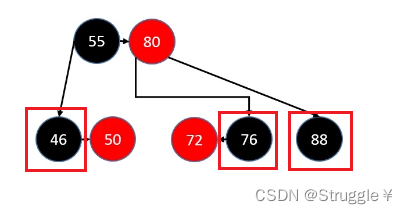
下面一一分析情况：

• 删除的是BLACK叶子节点，且sibling也为BLACK节点，大概就是下面几种样子：88的sibling是黑色的76

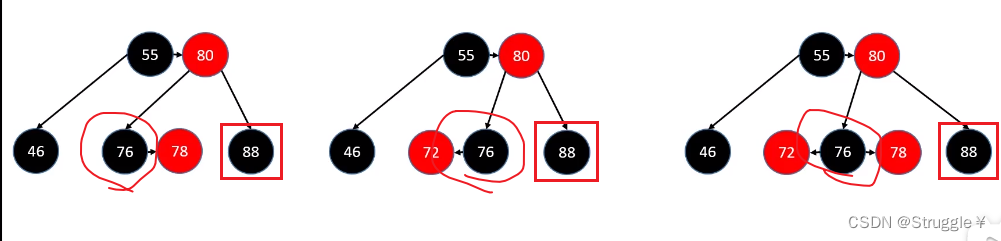
因为，删除叶子节点，站在B树的角度考虑此节点，那就是产生了下溢。回想一下B树中下溢是如何处理的（先看兄弟节点可不可以借一个，如果不能借，那就把父节点拉下来跟兄弟节点和自己合并）。

上面三种情况，都表示兄弟可以借一个节点给当前下溢节点。即，兄弟节点必须是黑色子节点且有红色子节点的情况下，才有能力借给你一个节点。有红色子节点，就三种情况。要么左边有，要么右边有，要么左右都有。

怎么借呢？按照之前的B树规则，大概就是父节点下去，从sibling里选一个上去。（需要旋转染色操作），具体步骤如下：

• 进行旋转操作（如果是LR，那就进行两次旋转操作；LL进行一次旋转操作）
• 旋转之后的中心节点继承原先父节点的颜色（也就是78继承80的颜色）
• 旋转之后，左右子节点染成黑色BLACK

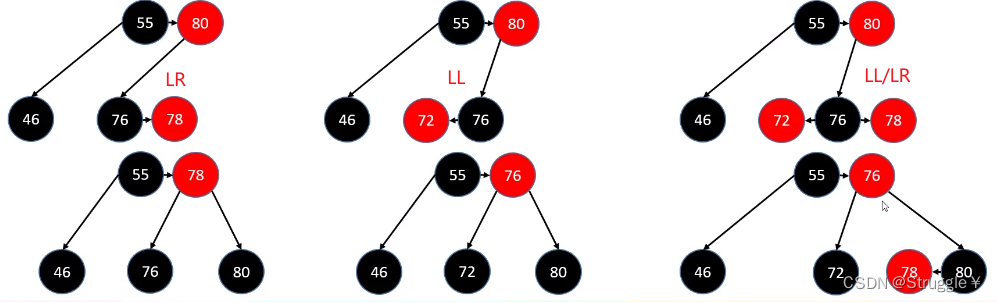
第三种情况，有两种旋转策略（LL/LR），会导致两种不同的结果。也就是说，红黑树不唯一，但是都满足红黑树的性质且满足二叉搜索树的性质，只不过样子可能不一样。

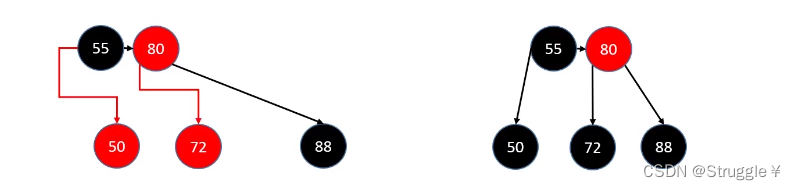
• 删除的是BLACK叶子节点，sibling也是黑色，但是没有红色子节点，没法借给我。就下图所示：
  
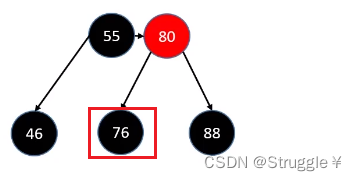
  这种情况怎么办呢？根据B树的经验，父节点下来合并（步骤就是：将sibling染成RED，然后将parent染成BLACK下来合并在一块）

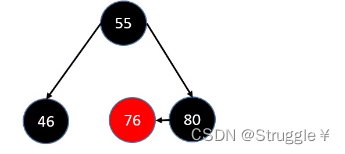
还有一种情况，就是88的父节点本身就是黑色（只有一个黑色节点），且sibling也借不出来，如下图所示：

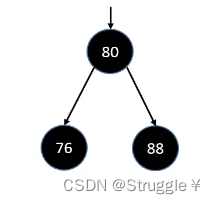
这种情况怎么处理呢？还是像之前那样，88删掉之后，父节点下来与sibling合并，并染色。

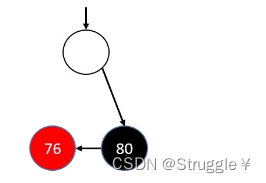
但是，此时一个问题出现了：原本父节点parent处，再次发生了下溢事件。怎么办？

答案也非常简单：只需要把parent当做新被删除的节点处理即可，也就是递归调用afterMove函数。跟前面讲的上溢递归调用是一类情况。

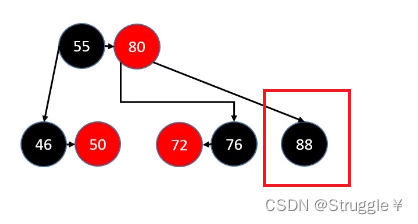
• 删除的是BLACK叶子节点，但是sibling是RED节点的时候。

为什么要区分sibling是红色还是黑色呢？那是因为：如果sibling是黑色的，sibling跟你是一行的。如果sibling是红色的，那么sibling一定是在父节点那一行，就像下图所示：88的sibling是红色的55。

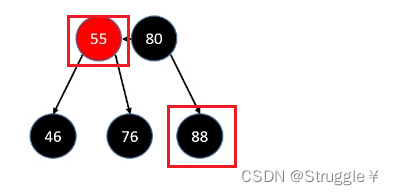
这时候，能借给你的就不能是你的sibling了，而是你sibling的子节点。这种情况我们如何处理呢？

答案是：强制让侄子节点变成兄弟节点。具体操作就是对88的parent80进行右旋转，让55变为这棵子树的根节点。然后80就可以指向76了，此时88和76就是兄弟节点了。这就又回到了sibling是黑色节点，但是不能借的情况。

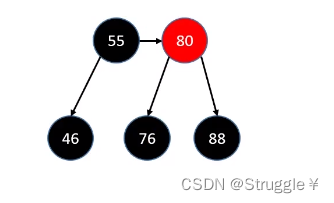
这种情况，上面已经讲过了，直接把88删掉，然后80染成黑色下来，sibling76节点染成红色，并与80融合成为一个新的B树节点。最终的效果就是下面：

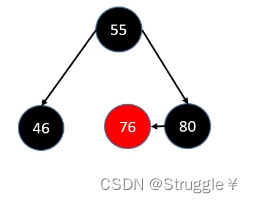
上述就是删除节点的所有情况！！！！！删除节点，真的很复杂！！！

红黑树平衡在哪？

AVL平衡的保障是平衡因子的存在。红黑树也是平衡二叉树，那么平衡在哪了？因为，我们在修复红黑树的时候，好像一直在旋转，染色。丝毫感觉不到平衡在哪？

当初遗留的困惑：为何红黑树的5条性质，就能保障红黑树是平衡的呢？

我们知道一点：红黑树的5条性质可以保证红黑树完完全全等价于4阶B树。就像下图一样：

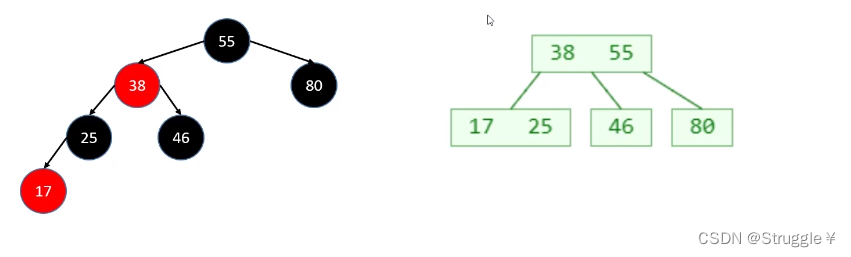
有人就会问了，左边的红黑树，一点也不平衡啊，还没有AVL树平衡呢！！！！

的确啊，红黑树没法像AVL树那样平衡。换句话说，AVL树是一种硬平衡树，而红黑树是一个软平衡树。

红黑树可以保证的平衡是：没有一条路径会大于其他路径的两倍。（路径：根节点到任意叶子节点的距离）

那有人就想说了，红黑树都没AVL树平衡，还学红黑树干嘛！之前还说红黑树比AVL树好，好在哪了呢？

AVL树和红黑树的对比

总结：AVL删除时，可能性能不好。红黑树虽然没AVL树平衡，但是平均性能会更好。因此实际应用中，红黑树用的更多。