关于求定积分的反函数的导数【认清原函数x变量和反函数x变量】

如图碰到该题该怎么解？

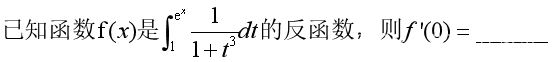
在纸上按①②③的顺序写出这个，其中①是最主要的

第②步和第③步就是在用反函数时要用到的逻辑思维，不是一起用的，你需要用②才去用②，你需要用③才去用③

---

在纸上先写出第①步，即

其中，

---

第②步，

由步骤①的在它的上方写它的原函数，等于左边的反变量x（也就是反函数的变量x）

---

第③步，

由步骤①的在它的下方写它的原函数，等于右边的原变量y（也就是原函数的变量y）

---

故，这道题我是这么解的：

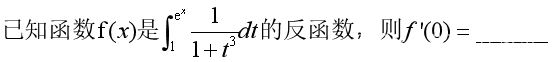
所以，我们在算这道题时要认清原函数的x变量和反函数的x变量：

题目的里的0是反函数的x变量

我们在运算中将原函数求导后得出的结果，里面的x还停留在原函数的x变量的阶段，

所以回过头来将里的0去等于原函数，逼出里面的原函数的x变量，将这个原函数的x变量代入 原函数求导后得出的结果，才是最终的答案。