1.图像的尺度
这里图像的尺度并非指图像的大小,而是指图像的模糊程度(σ) ,例如,人近距离看一个物体和远距离看一个物体模糊程度是不一样的,从近距离到远距离图像越来越模糊的过程,也是图像的尺度越来越大的过程。
2.尺度空间的作用
1.用机器视觉系统分析未知场景时,计算机并不预先知道图像中物体的尺度。我们需要同时考虑图像在多尺度下的描述,获知感兴趣物体的最佳尺度。
2.不同的尺度下都有同样的关键点,那么在不同的尺度的输入图像下就都可以检测出来关键点匹配,也就是尺度不变性。
图像的尺度空间表达指的就是图像在所有尺度下的描述。
3.多尺度表示
1.金字塔多分辨率
图像的金字塔化包括两个步骤,首先,图像经过一个低通滤波器进行平滑,然后,对这个平滑图像进行抽样(宽,高为原来的1、2)。

2.多尺度空间
信号的尺度空间有一个重要的特性是通过低通滤波器后,在大尺度上不会引入虚假结构。
两者都能有效地对图像进行多尺度表达,但金字塔多分辨率缺少坚实的理论基础,不能得到图像的最佳尺度,同样也不具有特征的尺度不变性。
后者与前者的主要区别在与,多尺度空间在不同尺度(σ)上有相同的分辨率,即可以理解为,在不同的尺度上图像的大小是相同的。
一幅图像的尺度空间 L(x, y, σ), 定义为原始图像 I(x,y) 与一个可变尺度的2维高斯函数G(x, y, σ)卷积运算。
即尺度空间形式表示为:

其中
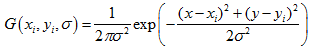
高斯尺度空间具有的性质
1.加权平均和有限孔径效应
2.层叠平滑
3.局部极值递减性
4.尺度伸缩不变性
4.最佳尺度选择
感兴趣图像结果在不同尺度上的响应是不同的,例如,同样一副含有人手的图像,当我们的感兴趣结构是人的手指,或者是人的手臂时,所需图像的最佳尺度是不同的。

在实际工作中,可以通过经验选择来确定最佳尺度。
5.多尺度特征匹配
在提取图像的特征时,如果采取固定尺度的特征检测,就会得到偏向该尺寸的检测结果,而漏检很多其他尺度的特征。
为了是不同尺度上图像中相同的特征被检测出,需要在图像的多个尺度上进行检测和匹配。
————————————————
版权声明:本文为CSDN博主「Lindsay.Lu丶」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/ljyljyok/article/details/87854453








 图像的尺度空间描述了图像的模糊程度,而非大小,它通过高斯滤波和尺度变化实现多尺度表示。尺度空间的作用在于处理尺度不确定性,确保特征的尺度不变性。多尺度表示如图像金字塔虽有效,但缺乏最佳尺度选择和尺度不变性。最佳尺度选择通常依赖于感兴趣的图像特征。多尺度特征匹配能提高图像检测的全面性,避免固定尺度带来的遗漏。
图像的尺度空间描述了图像的模糊程度,而非大小,它通过高斯滤波和尺度变化实现多尺度表示。尺度空间的作用在于处理尺度不确定性,确保特征的尺度不变性。多尺度表示如图像金字塔虽有效,但缺乏最佳尺度选择和尺度不变性。最佳尺度选择通常依赖于感兴趣的图像特征。多尺度特征匹配能提高图像检测的全面性,避免固定尺度带来的遗漏。
















 2919
2919

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








