Slope Trick：解决一类凸代价函数DP优化

【前言】

在补Codeforce的DP时遇到一个比较新颖的题，然后在知乎上刚好 hycc 桑也写了这道题的相关题解，这里是作为学习并引用博客的部分内容

这道题追根溯源发现2016年这个算法已经在APIO2016烟花表演与Codeforces 713C引入，自那之后似乎便销声匿迹了。相关题型数量也较少，因而在这里结合前辈们的工作做一些总结。---by hycc

问题引入：Codeforces 713C

题目链接：Here

题意：

• 给定 \(n\) 个正整数 \(a_i\) ，每次操作可以选择任意一个数将其 \(+1\) 或 \(-1\) ，问至少需要多少次操作可以使得 \(n\) 个数保持严格单增。

• 数据范围：\(1\le n\le 3000,1\le a_i\le 10^9\)

对我来说这道题其实和曾经写过的 POJ-3666：求不升的DP是一样的

这个题是求升序的DP，那么有什么变化呢

不升的条件是：\(a_i -a_j \ge 0\)

升序的条件是：\(a_i -a_j \ge i - j\) 对任意 \(i,j\) 均满足

有没有理解到什么？移项有：\(a_i - i \ge a_j - j\)

所以将 \(a\)​ 数字变形一下就和POJ3666就是一个题！

【AC Code】

const int N = 3100;
int n, m;
ll f[N][N], a[N], b[N];
int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
        a[i] = a[i] - i;
        b[i] = a[i];
    }
    sort(b + 1, b + 1 + n);
    m = 1;
    for (int i = 2; i <= n; ++i) if (b[i] != b[i - 1]) b[++m] = b[i];
    memset(f, 0, sizeof(f));
    for (int i = 1; i <= n; ++i) {
        ll Min = LLONG_MAX;
        for (int j = 1; j <= m; j++) {
            Min = min(Min, f[i - 1][j]);
            f[i][j] = abs(b[j] - a[i]) + Min;
        }
    }
    ll ans = LLONG_MAX;
    for (int i = 1; i <= m; ++i) ans = min(ans, f[n][i]);
    cout << ans << "\n";
}

当然上面说的思路并不是本篇博客实际想表达，以下才是正文

对于朴素的 \(\mathcal{O}(n^2)\ DP\)​ ：

一个显然的性质：如果不是“严格单增”而是“严格非降”，那么最终形成的严格非降序列，其中每个元素一定属于 \(\{a_i\}\)​

将元素离散化后可以设计 \(f_{i,j}\) 表示到第 \(i\) 个数取 \(j\) 的最少操作数

那么有转移 \(f_{i,j} = \min\limits_{k\le j}f_{i-1,k} + | a_i - j|\)​ ，记录 \(f_{i-1,*}\)​ 的前缀 \(\min\)​ 即可做到 \(\mathcal{O}(n^2)\)​

至于如何做到“严格非降”，\(a_{i-1} < a_i,a_{i -1} \le a_i - i,a_{i-1}-(i-1)\le a_i - i\)

于是令 \(a_i = a_i - i\) 即可。

赛后的评论区中出现了一种 \(\mathcal{O}(Nlog\ N)\) 的做法，也就是 Slope Trick算法的第一次现身(？)

---

Slope Trick：解决一类凸代价函数的DP优化问题

当序列DP的转移代价函数为

连续
分段线性函数
凸函数

时，可以通过记录分段函数的最右一段 \(f_r(x)\) 以及其分段点 \(L\)​ 实现快速维护代价的效果。

如：\(f(x)=\left\{\begin{array}{rr} -x-3 & (x \leq-1) \\ x & (-1<x \leq 1) \\ 2 x-1 & (x>1) \end{array}\right.\)

可以仅记录 \(f_r(x) = 2x - 3\) 与分段点 \(L_f = \{-1,-1,1\}\) 来实现对该分段函数的存储。

注意：要求相邻分段点之间函数的斜率差为 \(1\) ，也就是说相邻两段之间斜率差 \(\ge 1\) 的话，这个分段点要在序列里出现多次。

优秀的性质：

\(F(x),G(x)\) 均为满足上述条件的分段线性函数，那么 \(H(x) =F(x)+G(x)\) 同样为满足条件的分段线性函数，且 \(H_r(x) = F_r(x) + G_r(x),L_H = L_F \bigcup L_G\) 。

该性质使得我们可以很方便得运用数据结构维护 \(L\)​ 序列。

回顾：Codeforces 713C

转移方程为 \(f_{i,j} = \min\limits_{k\le j}f_{i-1,k} + |a_i - j|\)​​

令 \(F_{i}(x)=f_{i, x}, G_{i}(x)=\min\limits _{k \leq x} f_{i-1, k}=\min \limits_{k \leq x} F_{i-1}(k)\)

那么有 \(F_i(x) = G_i(x) + |x -a_i|\) ，其中 \(F_i,G_i\) 均为分段线性函数。

\(G_i\) 求的是 \(F_{i-1}\) 的关于函数值的前缀最小值，由于 \(F_{i-1}\) 是一个凸函数，因而其最小值应该在斜率 \(=0\) 处取得，其后部分可以舍去。

而每次由 \(G_i(x)\) 加上 \(|x-a_i|\) ，等价于在 \(L\) 中添加两个分段点 \(\{a_i,a_j\}\)

因而 \(G_i\) 各段的函数斜率形如 \(\{...,-3,-2,-1,0\}\) ，加上 $|x-a_i| $后斜率变为 \(\{...,-3,-2,-1,0,1\}\) ，因而需要删除末尾的分段点。

具体实现中：使用大根堆维护分段点单调有序，每次加入两个 \(a_i\) ，再弹出堆顶元素。

总复杂度 ：\(\mathcal{O}(n\ log\ n)\)

---

\[QAQ \]

---

Codeforces 1534G

题意：

一个无限大的二维平面上存在 \(n\)​ 个点 \((x_i,y_i)\)​ 均需要被访问一次，从 \((0,0)\) 出发，每次可以向右或向上移动一个单位。

可以在任意位置 \((X,Y)\) 访问 \((x_i,y_i)\) 并付出 \(\max\{|X-x_i|,|Y-y_i|\}\) 的代价(访问后依然留在 \((X,Y)\) )。同一位置可以访问多个点。

问：至少需要花费多少代价才能使得所有点均被访问？

数据范围： \(1\le n\le 800000,0\le x_i,y_i\le 10^9\)

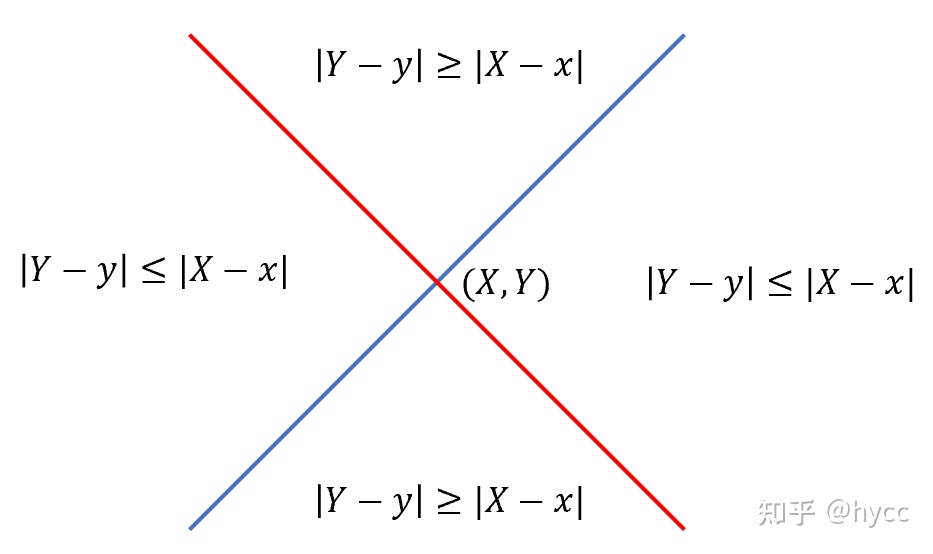
结合上图可以看出，对于点 \((X,Y)\) ，一定会选择路径与直线 \(x+y=X+Y\)(红线)的交点 \((x,y)\) 处作为访问的发起点(在这条线上 \(|X-x| = |Y-y|\) )。

考虑到这条红线是倾斜的，因而将坐标系顺时针翻转 \(45^°\)​，即 \((x+y,x-y)\) 代替 \((x,y)\)

此时，每次移动变为 \((x+1,y-1)\)​ 或 \((x+1,y+1)\)

把所有点按新的 \(x\) 坐标排序，即可转为序列上的问题。

设值域为 \(M\) ，则很容易写出 \(\mathcal{O}(nM)\) 的转移方程：

\(f_{i,Y}\) 表示从左到右考虑到横坐标为 \(x_i\) 的所有点，当前路径到了 \((x_i,Y)\) 的最小代价，

那么有

$f_{i,Y}=\min\limits_{Y-\left|x_{i}-x_{i-1}\right|\leq k\leq Y+\left|x_{i}-x_{i-1}\right|}f_{i-1, k}+\sum\limits_{(x, y), x=x_{i}}|Y-y| $​​

同样，设 \(F_{i}(x)=f_{i, x}, G_{i}(x)=\sum\limits_{x-\left|x_{i}-x_{i-1}\right| \leq k \leq x+\left|x_{i}-x_{i-1}\right|} f_{i-1, k}\)​

那么 \(F_{i}(x)=G_{i}(x)+\sum_{\left(x^{\prime}, y^{\prime}\right), x^{\prime}=x_{i}}\left|x-y^{\prime}\right|\)

---

主要问题在于 \(G_i(x)\) 的维护，是取一个区间范围 \([L,R]\) 内的最小值。

若斜率为 \(0\) 的两端点在 \([L,R]\) 内，那么直接取最小值即可。

若斜率为 \(0\) 的两端点在 \(L\) 左侧，需要取 \(L\) 处的值作为最小值。

若斜率为 \(0\) 的两端点在 \(R\)​ 右侧，需要取 \(R\) 处的值作为最小值。

因而，需要维护斜率为 \(0\) 的折线的两侧分割点 \((a,b)\) ，同时还需要支持从斜率为 \(0\) 处向两侧访问，因而使用小根堆与大根堆分别维护 \(b\) 右侧以及 \(a\) 左侧的点。

每次添加新的分割点时，根据新分割点与 \(a,b\) 的大小关系决定插入小根堆or大根堆，同时调整 \(a,b\) ，每次调整复杂度是 \(\mathcal{O}(1)\) 的(从小根堆中取出塞入大根堆或反之)

【AC Code】借用 jiangly的代码

#include <bits/stdc++.h>
using i64 = long long;
int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);
    int n;
    std::cin >> n;
    std::vector<std::pair<int, int>> a;
    for (int i = 0; i < n; i++) {
        int x, y;
        std::cin >> x >> y;
        a.emplace_back(x + y, x);
    }
    std::priority_queue<i64> hl;
    std::priority_queue<i64, std::vector<i64>, std::greater<>> hr;
    for (int i = 0; i < n + 5; i++) {
        hl.push(0);
        hr.push(0);
    }
    i64 tag = 0, mn = 0;
    int last = 0;
    std::sort(a.begin(), a.end());
    for (auto [s, x] : a) {
        int d = s - last;
        last = s;
        tag += d;
        if (x <= hl.top()) {
            mn += hl.top() - x;
            hl.push(x);
            hl.push(x);
            hr.push(hl.top() - tag);
            hl.pop();
        } else if (x >= hr.top() + tag) {
            mn += x - (hr.top() + tag);
            hr.push(x - tag);
            hr.push(x - tag);
            hl.push(hr.top() + tag);
            hr.pop();
        } else {
            hl.push(x);
            hr.push(x - tag);
        }
    }
    std::cout << mn << "\n";
    return 0;
}