耐心看完不会让你失望的动态规划

动态规划概述

当我们遇到一个问题的时候，如何确定是需要使用动态规划来做的，动态规划题目有什么特点：

• 1、计数

- 有多少种方式能走到右下角
- 有多少种方法选出k个数使得和是Sum

• 2、求最大值,最小值

- 从左上角走到右下角路径的最大数字和
- 最长上升子序列长度

• 3、求存在性

- 取石子游戏，先手是否必胜
- 能不能选出K个数使得和是Sum

举例：

• 给定一个矩阵网格，一个机器人从左上角出发，每次可以向下或者向右走一步
  • 问题1：求有多少种方式可以走到右下角
  • 问题2：输出所有走到右下角的路径
• 分析：上面两个问题那个问题可以使用动态规划求解，问题1，因为符合上面的动态规划题目的特点。

动态规划用于求取全局最优解，贪心算法可以求取局部最优解，有时候使用贪心算法通过求取局部最优解，可以得到全局最优解，如果贪心算法能满足要求，就不要用动态规划，这就是所谓的：杀鸡焉用牛刀！！！！

如何使用动态规划算法：力扣322题（中等）

通过一个例子来分析一下吧：

• 问题描述：你有三种硬币，分别为面值2元，5元，7元，每种硬币的数量足够过
• 要求：买一本书需要27元，如何用最少的硬币组合刚好付清，不需要对方找钱
• 问题分析：求取的最小值的问题，最值问题可以使用动态规划求解

注意：如果使用贪心算法，能不能求解那，显然是不太可以，因为最后得到的不是全局最优解，还有可能是无解。

使用动态规划算法可以分为四步：

第一步：确定状态

状态在动态规划中是非常重的，牵涉到这道题你能不能解得出来

简单来说，解动态规划的时候需要开辟一个数组（可能是一维的，也可能是二维的，具体问题具体分析），
数组中的每个元素代表什么，f[i]，或者f[i][j]

确定状态需要需要两个意识：
- 最后一步
	- 使用上面的例子，虽然我们不知道最优策略是什么，但是最优策略的最后一步肯定是需要K枚硬币，
	- K枚硬币的值加起来为27
	- 第一枚硬币为a1，，，第k枚硬币为ak
	- 关键点1：我们不用关心前面的K-1枚硬币是怎么拼出的（可能是一种方法，也可能是很多种），
			  我们只需要确定它拼出来了，能实现。
	- 关键点2：因为是最优策略，所以前面K-1枚硬币的数量一定是所有方法中数量最少的，否则就不是
	 		  最优策略了
- 子问题
	- 现在我们的要求就是：最少能用多少枚硬币拼出27-ak
	- 原问题：最少用多少枚硬币拼出27
	- 原问题和子问题的要求是一样的，只不过是规模变小了：27-ak
	- 我们要找的状态转移方程为：f(X)=最少用多少硬币拼出X
	- 因为我们不知道最后一枚硬币的值ak是多少，可能为2，也可能为5或者7
		- 如果为2：f(27)=f(27-2)+1，加上最后一枚硬币为2
		- 如果为5：f(27)=f(27-5)+1，加上最后一枚硬币为5
		- 如果为7：f(27)=f(27-7)+1，加上最后一枚硬币为7
	- 最终状态转移方程为：f(27)=min{f(27-2),f(27-5),f(27-7)}
通过状态分析最后得出状态转移方程

• 最后一步：
  

第二步：状态转移方程

• 设状态f[X]=最少用多少枚硬币拼出X
• 对于任意X，f(X)=min{f(X-2)+1,f(X-5)+1,f(X-7)+1}
  

第三步：初始条件和边界情况

• 对于状态转移方程：f(27)=min{f(27-2)+1,f(27-5)+1,f(27-7)+1}
• 问题：如果X-2，X-5，X-7小于0怎么办，什么时候停下来
• 分析：如果拼不出Y，就定义f[Y]=正无穷
• 举例：f[1]=min{f[1-2]+1,f[1-5]+1,f[1-7]+1}=正无穷，表示拼不出来。

使用状态方程算不出来，而我又需要的值，定义为正无穷。

• 为什么是正无穷：因为我们需要的是最小值，而且不知道需要拼出的数是多大，需要多少枚硬币可以拼出，选择一个较大数作为比较，更加方便！！！
• 初始条件：f[0]=0

这个初始条件需要具体问题具体分析，针对这个问题，如果拼出0元，则使用0个硬币，不可能为负。

• 有了初始条件和状态转移方程，我们就可以计算f[1],f[2],....,f[27]
• 边界问题主要是为了防止数组越界发生异常

第四步：计算顺序

• 动态规划要求：当我们求解下一个状态的时候，当前状态已经计算出结果了，而且是最优的，这样求解出来的才是全局最优的。

• 当我们计算f[X]的时候，f[X-2]，f[X-5]，f[X-7]，已经得到结果，如果能被表示出来就是最优的结果，如果不能被表示出来就用正无穷代替。

• 拼出X所需的最少硬币数：f(X)=min{f(X-2)+1,f(X-5)+1,f(X-7)+1}

• 初始条件：f(0)=0

• 然后计算：f(1)，f(2)，…，f(27)
  

时间复杂度分析：

• 通过上面的分析，每进行一步，都要尝试三种硬币，一共27步：27*3
• 时间复杂度：n*m

代码实现：

 public static int minCoins(int[] coins,int value){
        if(value==0){
            return 0;
        }
        //因为0~value，使用数组表示，定义数组的长度就是value+1
        //如果有解，数组对应位置存放的值就是解，没解的的位置存储一个最大值，最后使用-1替换所有的最大值
        int[] f=new int[value+1];
        //初始条件：f[0]=0
        for(int i=1;i<f.length;i++){
            //给数组初值，因为我们要找的是最小值，为了方便，不能被表示出来的面值使用无穷大表示
            f[i]=Integer.MAX_VALUE;
            //如果能被表示，就使用状态转移方程求取最优解，并给数组重新赋值
            for(int j=0;j<coins.length;j++){
                //注意：只有当i的值大于等于coins的值并且f[i-coins[j]]这个面值能别表示出来，才可以
                if(i>=coins[j]&&f[(i-coins[j])]!=Integer.MAX_VALUE){
                    f[i]=Math.min(f[i-coins[j]]+1,f[i]);//状态转移方程：重新赋值
                }
            }
        }
        //替换MAV_VALUE为-1，题目要求，表示不出来的值返回-1
        if(f[value]==Integer.MAX_VALUE){
            f[value]=-1;
        }
        return f[value];
    }

最后在啰嗦一句，为什么使用MAX_VALUE：

因为我们求取的是最小值，如果给的面值（待表示的值）很大，那么我们就需要很多的硬币才能表示出这个面值，如果我们使用无穷大最为对比，那么我们就不用担心，我们使用的硬币数会超过这个值，这样会给我们带来便捷，其实如果要求的面值不大，这个数设置成小一点的正整数也可以

提醒：如果求取最小值，最好选用一个最大值作比较，如果选用最大值，最好选择一个最小值作比较。

案例1：力扣62题（中等）

为了熟悉动态规划，我们再来看一个例题，上面的例题我们使用的是一维数组来保存我们要求取的结果，这个我们这个例子需要用一个二维数组来保存我们要求取的结果：

• 问题描述：给定m行n列的网络，是有一个机器人从左上角(0,0)出发，每一步可以向下或者向右一步。
• 要求：多少种方式可以走到右下角
• 问题分析：有关计数的问题，可以使用动态规划求解

使用动态规划算法可以分为四步：

第一步：确定状态

最后一步：无论机器人使用何种方式走到右下角，最后挪动的哪一步，要么是向右，要么是向下
- 注意：(m,n)的网格，最后的那个网格坐标是(m-1,n-1)。
- 机器人的最后一步前的坐标为：(m-2,n-1)或者(m-1,n-2)
- 假如机器人有X种方式走到(m-2,n-1)，有Y种方式走到(m-1,n-2)，则走到(m-1,n-1)就有X+Y种方式
子问题：如下图
- 如果最后一步之前在(m-2,n-1),则子问题就是有多少种方式可以走到黄色区域的右下角
- 如果最后一步之前在(m-1,n-2),则子问题就是有多少种方式可以走到红色区域的右下角

通过子问题和最后一步，我们就可以确定出状态方程

注意：这次动态规划求解相比于上面那道题，我们需要开辟一个二维数组，因为我们需要使用两个变量。

第二步：状态方程

• 对于任意一个格子(i,j)：
  

第三步：初始条件和边界情况

• 有了状态方程，加上初始条件这道题一般也就出来了，边界情况只是防止数组越界的发生。
• 初始条件：f[0][0]=0，因为只有一种方式走到左上角

第四步：计算顺序

• 由于动态规划，后面的步骤需要用到前面的值，所以在计算后面的值的时候，需要保证前面的能用到的值都已经计算完成，所以我们要先计算行的值，在计算列的值(也就是一行一行的计算)
• 注意：走到第0行和第0列的都只有一种方法。

代码实现：

public static int countStep(int m,int n){
        //0~m-1   0~n-1   都可以表示到
        int[][] countArr=new int[m][n];
        //第0行，第0列的值为1
        for(int i=0;i<n;i++){
            countArr[0][i]=1;
        }
        for(int i=0;i<m;i++){
            countArr[i][0]=1;
        }
        //给计数矩阵赋值：先计算行
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                countArr[i][j]=countArr[i-1][j]+countArr[i][j-1];
            }
        }
        return countArr[m-1][n-1];
    }

• 也可以这样写：

public static int countStep(int m,int n){
       //0~m-1   0~n-1   都可以表示到
       int[][] countArr=new int[m][n];
       //给计数矩阵赋值：先计算行
       for(int i=0;i<m;i++){
           for(int j=0;j<n;j++){
               // 第0行，第0列的值为1
               if(i==0||j==0){
                   countArr[i][j]=1;
               }else {
                   countArr[i][j]=countArr[i-1][j]+countArr[i][j-1];
               }
           }
       }
       return countArr[m-1][n-1];
   }

案例2：力扣403题（困难）

• 问题描述：有n个石头分别在x轴0~n-1位置上，一只青蛙在石头0上，想跳到n-1石头上。
• 要求： 在第i块石头上最多可以向右跳距离a[i]，问青蛙能够跳到石头n-1上。
• 问题分析：有关存在性的问题，可以使用动态规划求解
• 示例：

- 输入：a=[2,3,1,1,4]
- 输出：True
- 分析：在第0块石头上可以跳2块，第1块石头上可以跳3块，以此类推，看看能否跳到第4块石头上

- 输入：a=[3,2,1,0,4]
- 输出：False
- 分析：在第0块石头上可以跳3块，第1块石头上可以跳2块，以此类推，看看能否跳到第4块石头上

最多可以跳3块：也就是可以跳1块，2块，3块

使用动态规划算法可以分为四步：

第一步：确定状态

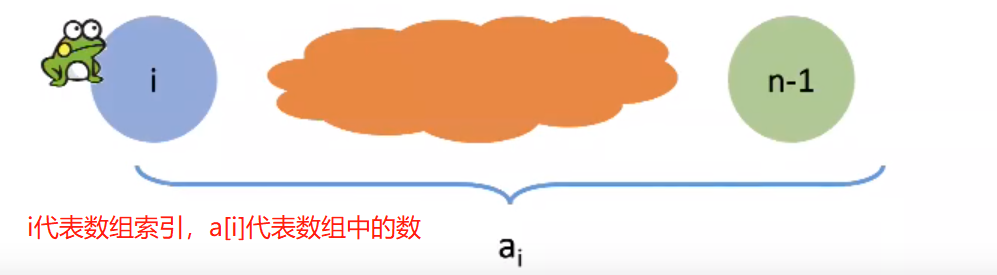
最后一步：如果青蛙能能跳到最后一块石头n-1，我们考虑它跳的最后一步
- 这一步是从石头n-i=跳过来的，最后一步跳跃的距离为i，i小于等于a[i]，a[i]<n-1
- 还需要两个条件同时满足
	- 青蛙能跳到石头i 
	- 最后一步跳跃的最大距离：n-i-1<=a[i]

子问题：
- 青蛙能不能跳到石头n-i
- 之前的问题是：青蛙能不能跳到石头n-1

第二步：状态方程

• 设f[j]表示青蛙能不能跳到石头j
  
• 这个转移方程是不是不太好理解，回来图解一下，就知道咋回事了。
  

第三步：初始条件和边界情况

• 初始条件：f[0]=true，因为青蛙一开始就在石头0

第四步：计算顺序

• 这个和之前的一样，被用到的值要先计算出来，顺序就是从左向右

代码实现：

public static boolean jumpGame(int[] arr){
       //构建一个一位数组，用于存放值
       boolean[] res=new boolean[arr.length];
       //初始值
       res[0]=true;
       for(int j=1;j<res.length;j++){
           //先预设为false
           res[j]=false;
           //枚举出前面所有的值
           for(int i=0;i<j;i++) {
               //判断条件1：前面的能被表示出来，如果前面的都表示不出来，当前就无须在表示
               //判断条件1：枚举出前面的所有值，看看是否有一个能到达该位置，有一个即可！！！
               if (res[i] && i + arr[i] >= j) {
                   res[j] = true;
               }
           }
       }
       //返回结果
       return res[arr.length-1];
   }

后记

本篇博客参考九章算法的动态规划公开课，里面也添加了自己的理解，仅供参考。