数论模板-素数筛、约数、欧拉函数

数论

质数的判定：试除法

在大于1的整数中，如果只包含1和本身这两个约数，就被称为质数/素数
一定为·O(sqrt(n))

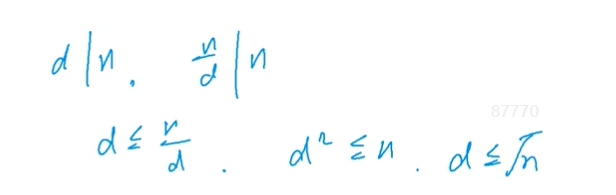
不推荐：
i*i<n 存在溢出风险
i<n/i 一定不会溢出
i<sqrt(n)每次都要调用函数

分解质因数：试除法

不一定为O(sqrt(n))
最好O(logn)，最坏O(sqrt(n))
根据算术基本定理，不考虑排列顺序的情况下，每个正整数都能够以唯一的方式表示成它的质因数的乘积。

n=p1^a1 x p2^a2 x p3^a3 x…… x pn^an

比如一个数16 在分解时先找到2这个质因子，然后由于16/2后还可以/2，所以会在2这个质因子上产生次方

不优化版本：从2~n 找到能整除的因子然后算次方
提前不满意这个不优化版本

这里有个性质：n中最多只含有一个大于sqrt(n)的因子。
证明通过反证法：如果有两个大于sqrt(n)的因子，那么相乘会大于n，矛盾。证毕
于是我们发现最多只有一个大于sqrt(n)的因子，对其进行优化。先考虑比sqrt(n)小的，代码和质数的判定类似
最后如果n还是>1，说明存在大于sqrt(n)的唯一质因子，输出即可。

#include <iostream>
void find(int n){
    int i;
    for(i=2;i<=n/i;i++){
        int s=0;
        while(n%i==0){
            n/=i;
            s++;
        }
        if(s>0)printf("%d %d\n",i,s);
    }
    if(n>1)printf("%d %d\n",n,1);//大于sqrt(n)的唯一质因子
}
int main(){
    int n;
    scanf("%d",&n);
    
    while(n--){
       int num;
       scanf("%d",&num);
       find(num);
       puts("");
    }
    
    return 0;
}

素数筛

1.最普通的筛法 O(nlogn)

依次筛去所有数的倍数，留下的都n/n是质数nlnn
n（n/2+n/+……+n/n）

质数定理：
1到n中有n/lnn个质数

#include <iostream>
const int N=1e6+100;
bool st[N];
int prim[N];
int cnt;
int n;
void get_primes2(){
    for(int i=2;i<=n;i++){

        if(!st[i]) primes[cnt++]=i;//把素数存起来
        for(int j=i;j<=n;j+=i){//不管是合数还是质数，都用来筛掉后面它的倍数
            st[j]=true;
        }
    }
}
int main(){
   
    scanf("%d",&n);
    get_prim();
    printf("%d",cnt);
    
    return 0;
}

2.诶氏筛法 O(nloglogn)

依次筛去所有质数的倍数，留下的都是质数nlnn/lnn=n

void get_primes1(){
    for(int i=2;i<=n;i++){
        if(!st[i]){
            primes[cnt++]=i;
            for(int j=i;j<=n;j+=i) st[j]=true;//可以用质数就把所有的合数都筛掉；
        }
    }
}

3.3.线性筛法 O(n)

核心：合数只会被最小质因子筛掉，每个数只会被筛一次，所以是线性的

void get_primes(){
    //外层从2~n迭代，因为这毕竟算的是1~n中质数的个数，而不是某个数是不是质数的判定
    for(int i=2;i<=n;i++){
        if(!st[i]) primes[cnt++]=i;
        for(int j=0;primes[j]<=n/i;j++){//primes[j]<=n/i:变形一下得到——primes[j]*i<=n,把大于n的合数都筛了就
        //没啥意义了
            st[primes[j]*i]=true;//用最小质因子去筛合数

            //1)当i%primes[j]!=0时,说明此时遍历到的primes[j]不是i的质因子，那么只可能是此时的primes[j]<i的
            //最小质因子,所以primes[j]*i的最小质因子就是primes[j];
            //2)当有i%primes[j]==0时,说明i的最小质因子是primes[j],因此primes[j]*i的最小质因子也就应该是
            //prime[j]，之后接着用st[primes[j+1]*i]=true去筛合数时，就不是用最小质因子去更新了,因为i有最小
            //质因子primes[j]<primes[j+1],此时的primes[j+1]不是primes[j+1]*i的最小质因子，此时就应该
            //退出循环，避免之后重复进行筛选。
            if(i%primes[j]==0) break;
        }
    }

}

约数

求约数：试除法

d是一个数约数，n/d也是一个数约数，枚举时可以只选较小的

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

void find(int n){
    vector<int>a;
    for(int i=1;i<=n/i;i++){
        if(n%i==0){
            a.push_back(i);
            if(n/i!=i)a.push_back(n/i);
        }
    }
    sort(a.begin(),a.end());
    
    for(auto t:a){
       cout<<t<<' ';
    }
}
int main(){
    int n;
    scanf("%d",&n);
    while(n--){
        int num;
        scanf("%d",&num);
        find(num);
        puts("");
    }
    return 0;
}

求约数个数

同时可求倍数个数
约数个数：

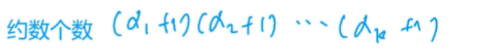
倍数个数：

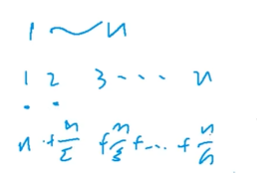
=nlogn个
int范围内约数最多的大概1500个

求约数之和

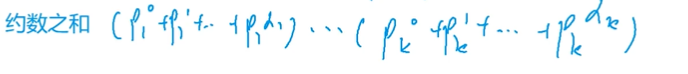
#include <iostream>
#include <unordered_map>

using namespace std;
const int mod=1e9+7;
typedef long long LL;


int main(){
    int n;
    scanf("%d",&n);
    
    unordered_map<int, int> hash;
    
    while(n--){
         
        int num;
        scanf("%d",&num);
        
        for(int i=2;i<=num/i;i++){
            
            while(num%i==0){
             num/=i;
             hash[i]++;
            }
            
            
        }
        if(num>1)hash[num]++;  
    }
    
    LL ans=1;
    
    for(auto t:hash){
       int p=t.first, a=t.second;                                                                                                                             a=t.second;
       LL pt=1;
       while(a--){
           pt=(pt*p+1)%mod;
       }
       ans=ans*pt%mod;
    }
    
 
    printf("%lld",ans);
    
    return 0;
}

求最大公约数：欧几里得算法O(logn)

也叫辗转相除法

若d可以整除a，d可以整除b，
则d可以整除a+b,d也可以整除ax+by

最大公约数gcd(a,b)=gcd(b,a mod b)

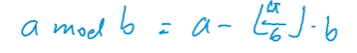
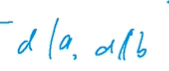
#include <iostream>
using namespace std;
int gcd(int a,int b){
   return b?gcd(b,a%b):a;
}
int main(){
    int n;
    scanf("%d",&n);
    while(n--){
      int a,b;
      scanf("%d%d",&a,&b);
      int ans=gcd(a,b);
      printf("%d\n",ans);
    }
    return 0;
}

欧拉函数

瓶颈在分解质因数上，分解质因数时间复杂度O(sqrt(n))

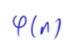
1到n中与n互质的数的个数
互质：即两个数不含有公共质因子

公式：与p的次数无关

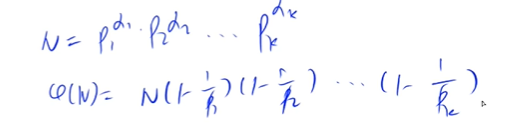
证明：

求欧拉函数

#include <iostream>
using namespace std;
int main(){
    int n;
    scanf("%d",&n);
    while(n--){
        int x;
        scanf("%d",&x);
       
        int res=x;
        
        for(int i=2;i<=x/i;i++){
            if(x%i==0){
                res=res/i*(i-1);
                while(x%i==0){
                    x/=i;
                }
            }
            
        }
        if(x>1)res=res/x*(x-1);
        printf("%d\n",res);
    }
    return 0;
}

筛法求欧拉函数

#include <iostream>
using namespace std;
const int N=1e6+100;
typedef long long LL;
int prime[N],cnt;
int phi[N];
bool st[N];
int n;
void get_euler(){
    
    phi[1]=1;
    
    for(int i=2;i<=n;i++){
        if(!st[i]){
            prime[cnt++]=i;
            phi[i]=i-1;
        }
        
        for(int j=0;prime[j]<=n/i;j++){
            st[i*prime[j]]=true;
            
            if(i%prime[j]==0){
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            }else{
                phi[i*prime[j]]=phi[i]*(prime[j]-1);
            }
            
        }
    }
    
    LL ans=0;
    
    for(int i=1;i<=n;i++){
        ans+=phi[i];
    } 
    
    printf("%lld",ans);
     
}
int main(){
    scanf("%d",&n);
    get_euler();
    return 0;
}

补充：欧拉定理

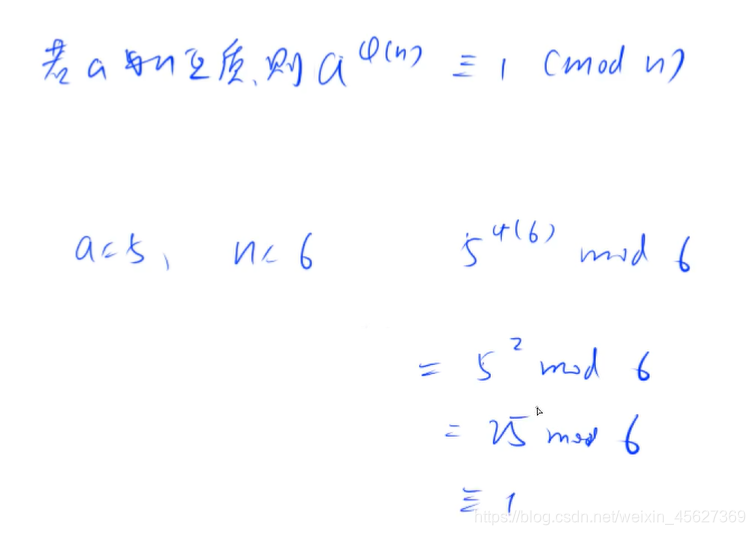
证明：

特例：
p为质数