图的基本概念，图的4种存储结构、基本操作详解

图

图的基本概念

图 $\mathrm{G}$ 由顶点集 $\mathrm{V}$ 和边集 $\mathrm{E}$ 组成，记为 $\mathrm{G}=(\mathrm{V},\mathrm{E})$ ，其中 $\mathrm{V}(\mathrm{G})$ 表示图 $\mathrm{G}$ 中顶点的有限非空集； $\mathrm{E}(\mathrm{G})$ 表示图 $\mathrm{G}$ 中顶点之间的关系（边）集合。若 V = { v 1 , v 2 , … , v n } {\rm V= \{ v_1,v_2,\dots,v_n \} } V={v1​,v2​,…,vn​} ，则用 $\left|\mathrm{V}\right|$ 表示图 $\mathrm{G}$ 中顶点的个数，$\mathrm{E}=\{(\mathrm{u},\mathrm{v})|u\in \mathrm{V},\mathrm{v}\in \mathrm{V}\}$，用 $\left|\mathrm{E}\right|$ 表示图 $\mathrm{G}$ 中边的条数。

注意：线性表可以是空表，树可以是空树，但图不可以是空图。就是说，图中不能一个顶点也没有，图的顶点集 $\mathrm{V}$ —定非空，但边集 $\mathrm{E}$ 可以为空，此时图中只有顶点而没有边。

下面是图的一些基本概念及术语。

图的示例

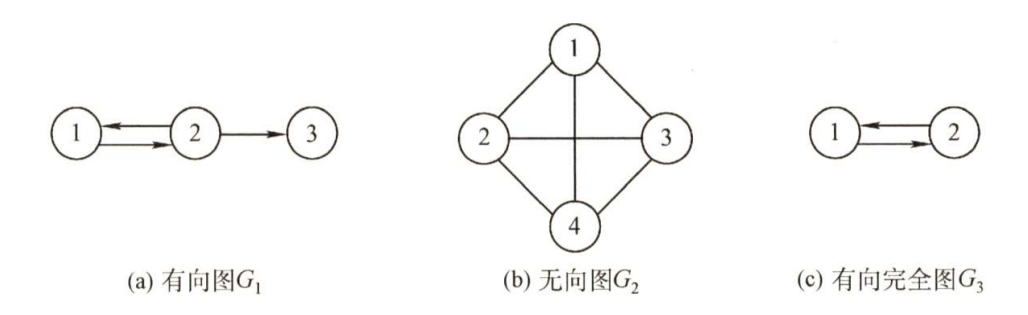
1.有向图

若 $\mathrm{E}$ 是有向边（也称弧）的有限集合时，则图 $\mathrm{G}$ 为有向图。弧是顶点的有序对，记为 $<\mathrm{v},\mathrm{w}>$ ，其中 $\mathrm{v},\mathrm{w}$ 是顶点， $\mathrm{v}$ 称为弧尾， $\mathrm{w}$ 称为弧头， $<\mathrm{v},\mathrm{w}>$ 称为从 $\mathrm{v}$ 到 $\mathrm{w}$ 的弧，也称 $\mathrm{v}$ 邻接到 $\mathrm{w}$ 。

上图(a)所示的有向图 ${\mathrm{G}}_1$ 可表示为：
G 1 = ( V 1 , E 1 ) V 1 = { 1 , 2 , 3 } E 1 = { < 1 , 2 > , < 2 , 1 > , < 2 , 3 > } {\rm G_1=(V_1,E_1)} \\ {\rm V_1}=\{ 1,2,3 \} \\ {\rm E_1=\{ <1,2>,<2,1>,<2,3> \} } G1​=(V1​,E1​)V1​={1,2,3}E1​={<1,2>,<2,1>,<2,3>}

2.无向图

若 $\mathrm{E}$ 是无向边（简称边）的有限集合时，则图 $\mathrm{G}$ 为无向图。边是顶点的无序对，记为 $(\mathrm{v},\mathrm{w})$ 或 $(\mathrm{w},\mathrm{v})$ 。可以说 $\mathrm{w}$ 和 $\mathrm{v}$ 互为邻接点。边 $(\mathrm{v},\mathrm{w})$ 依附于 $\mathrm{w}$ 和 $\mathrm{v}$ ，或称边 $(\mathrm{v},\mathrm{w})$ 和 $\mathrm{v},\mathrm{w}$ 相关联。

上图(b)所示的无向图 ${\mathrm{G}}_2$ 可表示为：
G 2 = ( V 2 , E 2 ) V 2 = { 1 , 2 , 3 , 4 } E 2 = { ( 1 , 2 ) , ( 1 , 3 ) , ( 1 , 4 ) , ( 2 , 3 ) , ( 2 , 4 ) , ( 3 , 4 ) } {\rm G_2=(V_2,E_2)} \\ {\rm V_2}=\{ 1,2,3,4 \} \\ {\rm E_2=\{ (1,2),(1,3),(1,4),(2,3),(2,4),(3,4) \}} G2​=(V2​,E2​)V2​={1,2,3,4}E2​={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}

3.简单图、多重图

一个图 $\mathrm{G}$ 如果满足：
1）不存在重复边；
2）不存在顶点到自身的边。
那么称图 $\mathrm{G}$ 为简单图。 上图中 ${\mathrm{G}}_1$ 和 ${\mathrm{G}}_2$ 均为简单图。若图 $\mathrm{G}$ 中某两个顶点之间的边数大于1条，又允许顶点通过一条边和自身关联，则称图 $\mathrm{G}$ 为多重图。多重图和简单图的定义是相对的。数据结构中仅讨论简单图。

4.完全图（也称简单完全图）

对于无向图， $\left|\mathrm{E}\right|$ 的取值范围为 $0$ 到 $\mathrm{n}(\mathrm{n}-1)/2$ ，有 $\mathrm{n}(\mathrm{n}-1)/2$ 条边的无向图称为完全图，在完全图中任意两个顶点之间都存在边。对于有向图， $\left|\mathrm{E}\right|$ 的取值范围为 $0$ 到 $\mathrm{n}(\mathrm{n}-1)$ ，有 $\mathrm{n}(\mathrm{n}-1)$ 条弧的有向图称为有向完全图，在有向完全图中任意两个顶点之间都存在方向相反的两条弧。
上图中 ${\mathrm{G}}_2$ 为无向完全图，而 ${\mathrm{G}}_3$ 为有向完全图。

5.子图

设有两个图 $\mathrm{G}=(\mathrm{V},\mathrm{E})$ 和 ${\mathrm{G}}^{\prime }=({\mathrm{V}}^{\prime },{\mathrm{E}}^{\prime })$ ，若 ${\mathrm{V}}^{\prime }$ 是 $\mathrm{V}$ 的子集，且 ${\mathrm{E}}^{\prime }$ 是 $\mathrm{E}$ 的子集，则称 ${\mathrm{G}}^{\prime }$ 是 $\mathrm{G}$ 的子图。若有满足 $\mathrm{V}({\mathrm{G}}^{\prime })=\mathrm{V}(\mathrm{G})$ 的子图 ${\mathrm{G}}^{\prime }$ ，则称其为 $\mathrm{G}$ 的生成子图。上图中 ${\mathrm{G}}_3$ 为 ${\mathrm{G}}_1$ 的子图。

注意：并非 $\mathrm{V}$ 和 $\mathrm{E}$ 的任何子集都能构成 $\mathrm{G}$ 的子图，因为这样的子集可能不是图，即 $\mathrm{E}$ 的子集中的某些边关联的顶点可能不在这个 $\mathrm{V}$ 的子集中。

无向图及其连通分量

6.连通、连通图和连通分量

在无向图中，若从顶点 $\mathrm{v}$ 到顶点 $\mathrm{w}$ 有路径存在，则称 $\mathrm{v}$ 和 $\mathrm{w}$ 是连通的。若图 $\mathrm{G}$ 中任意两个顶点都是连通的，则称图 $\mathrm{G}$ 为连通图，否则称为非连通图。无向图中的极大连通子图称为连通分量，在上图(a)中，图 ${\mathrm{G}}_4$ 有3个连通分量如上图(b)所示。假设一个图有 $\mathrm{n}$ 个顶点，如果边数小于 $\mathrm{n}-1$ ，那么此图必是非连通图；

思考，如果图是非连通图，那么最多可以有多少条边？
非连通情况下边最多的情况：由 $\mathrm{n}-1$ 个顶点构成一个完全图，此时再任意加入一条边则变成连通图。

7.强连通图、强连通分量

在有向图中，如果有一对顶点 $\mathrm{v}$ 和 $\mathrm{w}$ ，从 $\mathrm{v}$ 到 $\mathrm{w}$ 和从 $\mathrm{w}$ 到 $\mathrm{v}$ 之间都有路径，则称这两个顶点是强连通的。若图中任何一对顶点都是强连通的，则称此图为强连通图。有向图中的极大强连通子图称为有向图的强连通分量，图 ${\mathrm{G}}_1$ 的强连通分量下图所示。

思考，假设一个有向图有 $\mathrm{n}$ 个顶点，如果是强连通图，那么最少需要有多少条边？
有向图强连通情况下边最少的情况：至少需要 $\mathrm{n}$ 条边，构成一个环路。

注意：在无向图中讨论连通性，在有向图中讨论强连通性。

图G1的强连通分量

8.生成树、生成森林

连通图的生成树是包含图中全部顶点的一个极小连通子图。若图中顶点数为 $\mathrm{n}$ ，则它的生成树含有 $\mathrm{n}-1$ 条边。包含图中全部顶点的极小连通子图，只有生成树满足这个极小条件，对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路。在非连通图中， 连通分量的生成树构成了非连通图的生成森林。图 ${\mathrm{G}}_2$ 的一个生成树如下图所示。

图G2的一个生成树

注意：区分极大连通子图和极小连通子图。极大连通子图是无向图的连通分量，极大即要求该连通子图包含其所有的边；极小连通子图是既要保持图连通又要使得边数最少的子图。

9.顶点的度、入度和出度

在无向图中，顶点 $\mathrm{v}$ 的度是指依附于顶点 $\mathrm{v}$ 的边的条数，记为 $\mathrm{TD}(\mathrm{v})$ 。在上图(b)中，每个顶点的度均为3。对于具有 $\mathrm{n}$ 个顶点、 $\mathrm{e}$ 条边的无向图， ${\sum }_{\mathrm{i}=1}^{\mathrm{n}}\mathrm{TD}({\mathrm{v}}_{\mathrm{i}})=2e$ ，即无向图的全部顶点的度的和等于边数的2倍，因为每条边和两个顶点相关联。

在有向图中，顶点 $\mathrm{v}$ 的度分为入度和出度，
入度是以顶点 $\mathrm{v}$ 为终点的有向边的数目，记为 $\mathrm{ID}(\mathrm{v})$ ;
而出度是以顶点 $\mathrm{v}$ 为起点的有向边的数目，记为 $\mathrm{OD}(\mathrm{v})$ 。
在上图(a)中，顶点2的出度为2、入度为1。顶点 $\mathrm{v}$ 的度等于其入度与出度之和，即 $\mathrm{TD}(\mathrm{v})=\mathrm{ID}(\mathrm{v})+\mathrm{OD}(\mathrm{v})$ 。对于具有 $\mathrm{n}$ 个顶点、 $\mathrm{e}$ 条边的有向图，${\sum }_{\mathrm{i}=1}^{\mathrm{n}}\mathrm{ID}({\mathrm{v}}_{\mathrm{i}})={\sum }_{\mathrm{i}=1}^{\mathrm{n}}\mathrm{OD}({\mathrm{v}}_{\mathrm{i}})=\mathrm{e}$ ，即有向图的全部顶点的入度之和与出度之和相等，并且等于边数，这是因为每条有向边都有一个起点和终点。

10.边的权和网

在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值。这种边上带有权值的图称为带权图，也称网。

11.稠密图、稀疏图

边数很少的图称为稀疏图，反之称为稠密图。稀疏和稠密本身是模糊的概念，稀疏图和稠密图常常是相对而言的。一般当图 $\mathrm{G}$ 满足 $\left|\mathrm{E}\right|<\left|\mathrm{V}\right|\log \left|\mathrm{V}\right|$ ，可以将 $\mathrm{G}$ 视为稀疏图。

12.路径、路径长度和回路

顶点 ${\mathrm{v}}_{\mathrm{p}}$ 到顶点 ${\mathrm{v}}_{\mathrm{q}}$ 之间的一条路径是指顶点序列 ${\mathrm{v}}_{\mathrm{p}},{\mathrm{v}}_{{\mathrm{i}}_1},{\mathrm{v}}_{{\mathrm{i}}_2},\dots {\mathrm{v}}_{{\mathrm{i}}_{\mathrm{m}}}{\mathrm{v}}_{\mathrm{q}}$ ，当然关联的边也可理解为路径的构成要素。路径上边的数目称为路径长度。第一个顶点和最后一个顶点相同的路径称为回路或环。若一个图有 $\mathrm{n}$ 个顶点，并且有大于 $\mathrm{n}-1$ 条边，则此图一定有环。

13.简单路径、简单回路

在路径序列中，顶点不重复出现的路径称为简单路径。
除第一个顶点和最后一个顶点外，其余顶点不重复出现的回路称为简单回路。

14.距离

从顶点 $\mathrm{u}$ 出发到顶点 $\mathrm{v}$ 的最短路径若存在，则此路径的长度称为从 $\mathrm{u}$ 到 $\mathrm{v}$ 的距离。
若从 $\mathrm{u}$ 到 $\mathrm{v}$ 根本不存在路径，则记该距离为无穷（$\infty$）。

15.有向树

一个顶点的入度为0、其余顶点的入度均为1的有向图，称为有向树。

图的存储及基本操作

图的存储必须要完整、准确地反映顶点集和边集的信息。根据不同图的结构和算法，采用不同的存储方式将对程序的效率产生相当大的影响，因此所选的存储结构应适合于待求解的问题。

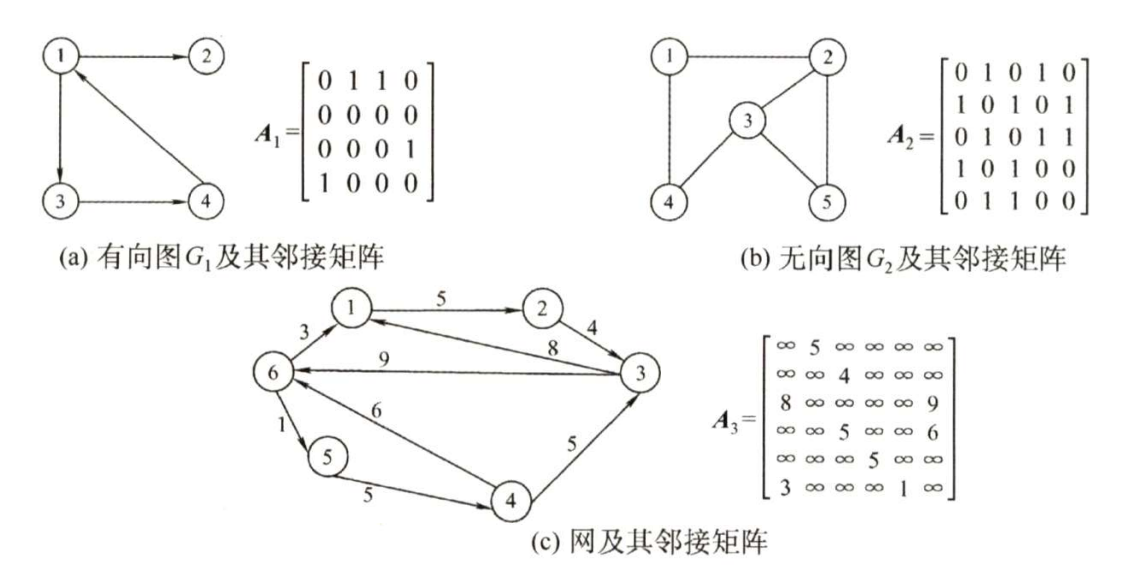
邻接矩阵法

所谓邻接矩阵存储，是指用一个一维数组存储图中顶点的信息，用一个二维数组存储图中边的信息（即各顶点之间的邻接关系），存储顶点之间邻接关系的二维数组称为邻接矩阵

结点数为 $\mathrm{n}$ 的图 $\mathrm{G}=(\mathrm{V},\mathrm{E})$ 的邻接矩阵 $\mathrm{A}$ 是 $\mathrm{n}\times \mathrm{n}$ 的。将 $\mathrm{G}$ 的顶点编号为 ${\mathrm{v}}_1,{\mathrm{v}}_2,\dots ,{\mathrm{v}}_{\mathrm{n}}$ 。若 $({\mathrm{v}}_{\mathrm{i}},{\mathrm{v}}_{\mathrm{j}})\in \mathrm{E}$ ，则 $\mathrm{A}[\mathrm{i}][\mathrm{j}]=1$ 否则 $\mathrm{A}[\mathrm{i}][\mathrm{j}]=0$ 。

$$\mathrm{A}[\mathrm{i}][\mathrm{j}]=\{\begin{array}{ll}1,& 若(v_i,v_j)或者<v_i,v_j>是E(G)中的边\\ 0,& 若(v_i,v_j)或者<v_i,v_j>不是E(G)中的边\end{array}$$
对于带权图而言，若顶点 ${\mathrm{v}}_{\mathrm{i}}$ 和 ${\mathrm{v}}_{\mathrm{j}}$ 之间有边相连，则邻接矩阵中对应项存放着该边对应的权值，若顶点 ${\mathrm{v}}_{\mathrm{i}}$ 和 ${\mathrm{v}}_{\mathrm{j}}$ 不相连，则用 $\infty $ 来代表这两个顶点之间不存在边：
$$\mathrm{A}[\mathrm{i}][\mathrm{j}]=\{\begin{array}{ll}{w}_{ij},& 若(v_i,v_j)或者<v_i,v_j>是E(G)中的边\\ 0或\infty ,& 若(v_i,v_j)或者<v_i,v_j>不是E(G)中的边\end{array}$$
有向图、无向图和网对应的邻接矩阵示例如下图所示。

有向图、无向图及网的邻接矩阵

图的邻接矩阵存储结构定义如下：

#define MaxVertexNum 100 //顶点数目的最大值

// VertexType，顶点的数据类型
// EdgeType，带权图中边上权值的数据类型
template<typename VertexType, typename EdgeType>
class MGraph {
private:
    VertexType Vex[MaxVertexNum];   //顶点表
    EdgeType Edge[MaxVertexNum][MaxVertexNum];  //邻接矩阵，边表
    int vexnum, arcnum;  //图的当前顶点数和弧数
};

注意：
1）在简单应用中，可直接用二维数组作为图的邻接矩阵（顶点信息等均可省略）。
2）当邻接矩阵的元素仅表示相应边是否存在时，$\mathrm{EdgeType}$ 可采用值为0和1的枚举类型。
3）无向图的邻接矩阵是对称矩阵，对规模特大的邻接矩阵可采用压缩存储。
4）邻接矩阵表示法的空间复杂度为 $\mathrm{O}({\mathrm{n}}^2)$ ，其中 $\mathrm{n}$ 为图的顶点数 $\left|\mathrm{V}\right|$ 。

图的邻接矩阵存储表示法具有以下特点∶
1）向图的邻接矩阵一定是一个对称矩阵 （并且唯一）。因此，在实际存储邻接矩阵时只需存储上（或下）三角矩阵的元素。
2）对于无向图，邻接矩阵的第 $\mathrm{i}$ 行（或第 $\mathrm{i}$ 列）非零元素（或非 $\infty$ 元素）的个数正好是顶点 $\mathrm{i}$ 的度 $\mathrm{TD}({\mathrm{v}}_{\mathrm{i}})$ 。
3）对于有向图，邻接矩阵的第 $\mathrm{i}$ 行非零元素（或非 $\infty$ 元素）的个数正好是顶点 $\mathrm{i}$ 的出度 $\mathrm{OD}({\mathrm{v}}_{\mathrm{i}})$ ； 第 $\mathrm{i}$ 列非零元素（或非 $\infty$ 元素）的个数正好是顶点 $\mathrm{i}$ 的入度 $\mathrm{ID}({\mathrm{v}}_{\mathrm{i}})$
4）用邻接矩阵存储图，很容易确定图中任意两个顶点之间是否有边相连。但是，要确定图中有多少条边，则必须按行、按列对每个元素进行检测，所花费的时间代价很大。
5）稠密图适合使用邻接矩阵的存储表示。
6）设图 $\mathrm{G}$ 的邻接矩阵为 $\mathrm{A}$ ， ${\mathrm{A}}^{\mathrm{n}}$ 的元素 ${\mathrm{A}}^{\mathrm{n}}[\mathrm{i}][\mathrm{j}]$ 于由顶点 $\mathrm{i}$ 到顶点 $\mathrm{j}$ 的长度为 $\mathrm{n}$ 的路径的数目。该结论了解即可，证明方法请参考离散数学教材。

邻接表法

当一个图为稀疏图时，使用邻接矩阵法显然要浪费大量的存储空间，而图的邻接表法结合了顺序存储和链式存储方法，大大减少了这种不必要的浪费。

所谓邻接表，是指对图 $\mathrm{G}$ 中的每个顶点 ${\mathrm{v}}_{\mathrm{i}}$ 建立一个单链表，第 $\mathrm{i}$ 个单链表中的结点表示依附于顶点 ${\mathrm{v}}_{\mathrm{i}}$ 的边（对于有向图则是以顶点 ${\mathrm{v}}_{\mathrm{i}}$ 为尾的弧），这个单链表就称为顶点 ${\mathrm{v}}_{\mathrm{i}}$ 的边表（对于有向图则称为出边表）。边表的头指针和顶点的数据信息采用顺序存储（称为顶点表），所以在邻接表中存在两种结点：顶点表结点和边表结点，如下图所示。

顶点表和边表结点结构

顶点表结点由顶点域（data）和指向第一条邻接边的指针（firstarc）构成，
边表（邻接表）结点由邻接点域（adjvex）和指向下一条邻接边的指针域（nextarc）构成。

无向图和有向图的邻接表的实例分别如下图所示。

无向图邻接表表示法实例 有向图邻接表表示法实例

图的邻接表存储结构定义如下：

#define MaxVertexNum 100 //图中顶点数目的最大值

struct ArcNode {    //边表结点
    int adjvex;     //该弧所指向的顶点的位置
    ArcNode *next;  //指向下一条弧的指针
    //InfoType info;//网的边权值
};

template<typename VertexType>
struct VNode {        //顶点表结点
    VertexType data;  //顶点信息
    ArcNode *first;   //指向第一条依附该顶点的弧的指针
};

template<typename VertexType>
class ALGraph { //ALGraph是以邻接表存储的图类型
private:
    VNode<VertexType> vertices[MaxVertexNum]; //邻接表
    int vexnum, arcnum; //图的顶点数和弧数
};

图的邻接表存储方法具有以下特点：
1）若 $\mathrm{G}$ 为无向图，则所需的存储空间为 $\mathrm{O}(\left|\mathrm{V}\right|+2\left|\mathrm{E}\right|)$ ；若 $\mathrm{G}$ 为有向图，则所需的存储空间为 $\mathrm{O}(\left|\mathrm{V}\right|+\left|\mathrm{E}\right|)$ 。前者的倍数2是由于无向图中，每条边在邻接表中出现了两次。
2）对于稀疏图，采用邻接表表示将极大地节省存储空间。
3）在邻接表中，给定一顶点，能很容易地找出它的所有邻边，因为只需要读取它的邻接表。
在邻接矩阵中，相同的操作则需要扫描一行，花费的时间为 $\mathrm{O}(\mathrm{n})$ 。
但是，若要确定给定的两个顶点间是否存在边，则在邻接矩阵中可以立刻查到，
而在邻接表中则需要在相应结点对应的边表中查找另一结点，效率较低。
4）在有向图的邻接表表示中，求一个给定顶点的出度只需计算其邻接表中的结点个数；但求其顶点的入度则需要遍历全部的邻接表。因此，也有人采用逆邻接表的存储方式来加速求解给定顶点的入度。当然，这实际上与邻接表存储方式是类似的。
5）图的邻接表表示并不唯一，因为在每个顶点对应的单链表中，各边结点的链接次序可以是任意的，它取决于建立邻接表的算法及边的输入次序。

十字链表

十字链表是有向图的一种链式存储结构。在十字链表中，对应于有向图中的每条弧有一个结点，对应于每个顶点也有一个结点。这些结点的结构如下图所示。

弧结点中有5个域：
尾域（tailvex）和头域（headvex）分别指示弧尾和弧头这两个顶点在图中的位置；
链域hlink指向弧头相同的下一条弧；
链域tlink指向弧尾相同的下一条弧;
info域指向该弧的相关信息。
这样，弧头相同的弧就在同一个链表上，弧尾相同的弧也在同一个链表上。

顶点结点中有3个域：
data域存放顶点相关的数据信息，如顶点名称；
firstin和 firstout两个域分别指向以该顶点为弧头或弧尾的第一个弧结点。

下图为有向图的十字链表表示法。注意，顶点结点之间是顺序存储的。

有向图的十字链表表示

在十字链表中，既容易找到 ${\mathrm{V}}_{\mathrm{i}}$ 为尾的弧，又容易找到 ${\mathrm{V}}_{\mathrm{i}}$ 为头的弧，因而容易求得顶点的出度和入度。图的十字链表表示是不唯一的，但一个十字链表表示确定一个图。

邻接多重表

邻接多重表是无向图的另一种链式存储结构。

在邻接表中，容易求得顶点和边的各种信息，但在邻接表中求两个顶点之间是否存在边而对边执行删除等操作时，需要分别在两个顶点的边表中遍历，效率较低。

与十字链表类似，在邻接多重表中，每条边用一个结点表示，其结构如下所示。

其中，
mark为标志域，可用以标记该条边是否被搜索过；
ivex和jvex为该边依附的两个顶点在图中的位置；
ilink指向下一条依附于顶点ivex的边；
jlink指向下一条依附于顶点jvex 的边，
info为指向和边相关的各种信息的指针域。

每个顶点也用一个结点表示，它由如下所示的两个域组成。

其中，data域存储该顶点的相关信息，firstedge域指示第一条依附于该顶点的边

在邻接多重表中，所有依附于同一顶点的边串联在同一链表中，由于每条边依附于两个顶点, 因此每个边结点同时链接在两个链表中。对无向图而言，其邻接多重表和邻接表的差别仅在于， 同一条边在邻接表中用两个结点表示，而在邻接多重表中只有一个结点。

下图为无向图的邻接多重表表示法。邻接多重表的各种基本操作的实现和邻接表类似。

无向图的邻接多重表表示

图的基本操作

图的基本操作是独立于图的存储结构的。而对于不同的存储方式，操作算法的具体实现会有着不同的性能。在设计具体算法的实现时，应考虑采用何种存储方式的算法效率会更高。

图的基本操作主要包括（仅抽象地考虑，故忽略掉各变量的类型）：

• Adjacent(G, x, y)：判断图 $\mathrm{G}$ 是否存在边 $<\mathrm{x},\mathrm{y}>$ 或 $(\mathrm{x},\mathrm{y})$ 。
• Neighbors(G, x)：列出图 $\mathrm{G}$ 中与结点 $\mathrm{x}$ 邻接的边。
• Insertvertex(G, x)：在图 $\mathrm{G}$ 中插入顶点 $\mathrm{x}$ 。
• DeleteVertex(G, x)：从图 $\mathrm{G}$ 中删除顶点 $\mathrm{x}$ 。
• AddEdge(G, x, y)：若无向边 $(\mathrm{x},\mathrm{y})$ 或有向边 $<\mathrm{x},\mathrm{y}>$ 不存在，则向图 $\mathrm{G}$ 中添加该边。
• RemoveEdge(G, x, y)：若无向边 $(\mathrm{x},\mathrm{y})$ 或有向边 $<\mathrm{x},\mathrm{y}>$ 存在，则从图 $\mathrm{G}$ 中删除该边。
• FirstNeighbor(G, x)：求图 $\mathrm{G}$ 中顶点 $\mathrm{x}$ 的第一个邻接点，若有则返回顶点号。若 $\mathrm{x}$ 没有邻接点或图中不存在 $\mathrm{x}$ ，则返回-1。
• NextNeighbor(G, x, y)：假设图 $\mathrm{G}$ 中顶点 $\mathrm{y}$ 是顶点 $\mathrm{x}$ 的一个邻接点，返回除 $\mathrm{y}$ 外顶点 $\mathrm{x}$ 的下一个邻接点的顶点号，若 $\mathrm{y}$ 是 $\mathrm{x}$ 的最后一个邻接点，则返回-1。
• Get_edge_value(G, x, y)：获取图 $\mathrm{G}$ 中边 $(\mathrm{x},\mathrm{y})$ 或 $<\mathrm{x},\mathrm{y}>$ 对应的权值。
• Set_edge_value(G, x, y, v)：设置图 $\mathrm{G}$ 中边 $(\mathrm{x},\mathrm{y})$ 或 $<\mathrm{x},\mathrm{y}>$ 对应的权值为 $\mathrm{v}$ 。

此外，还有图的遍历算法：按照某种方式访问图中的每个顶点且仅访问一次。图的遍历算法包括深度优先遍历和广度优先遍历。