背包问题及其优化-python实现

什么是背包问题

背包问题hi是组合优化的NP完全问题。问题的描述是：有一组物品，每种物品都有自己的重量和价值，现在挑选一些放到有重量限制的背包里，如何挑选物品才能使得背包里的物品总价值最大。背包问题广泛出现在商业、组合数学等场合。
针对物品的数量种类以及放置的规则，可以分为0-1背包问题，完全背包问题和多重背包问题等。

0-1背包问题

0-1背包问题是最基础的背包问题。其特点是，每件物品仅有一件，可以选择放或者不放入背包。

完全背包问题

完全背包问题是在0-1背包问题基础上扩展。不同于0-1问题的每件物品仅仅可以选择一个放入书包，在完全背包问题里，每种物品都有无限件可以用。

多重问题

多重问题是介于0-1背包和完全背包之间的。即每种物品有有限件，问题就可以描述为将哪些物品装入背包可使这些物品的体积总和不超过背包容量，且价值总和最大。

背包问题的求解

暴力搜索方法求解

背包问题的求解方法很多，最直观最容易想到的就是列举法，即暴力搜索方法。把物品的每种组合可能列出来，然后计算总价值找到最佳的组合。这种方法在物品种类和数量较少时候可以使用，但是随着物品种类数量的增大将，计算复杂的将急剧上升。一种改进方法是采用遗传算法对物品的是否放入背包进行基因编辑，然后在通过遗传交叉变异，求解结果。这种方法具有遗传算法的本身缺点，其中一个就是不能保证最优解。

贪婪算法

贪婪算法根据物品的价值或者价值比（价值除以重量），或者某一种合理的贪婪指标，按照次序贪婪地放入背包，贪婪算法无法得到最优解，甚至有时候性能极差。

动态规划解决背包问题

动态规划的基本思路是把大问题拆成小问题，通过寻找大问题与小问题的递推关系，解决一个个小问题，最终达到解决原问题的效果。在动态规划，递推步骤具有记忆性，通过填表法把已解决的子问题记录下来，在新问题需要用到的子问题可以直接提取，避免重复计算，从而节约时间。在问题满足最优性后，用动态规划的核心就是填表，当填表结束，最优解也就找到了。我们先来看看动态规划解决0-1背包问题。

0-1背包问题描述和建模

设有n个物品，每个物品的重量记为$w_i$，价值记为$v_i$，背包的容量为$C$。设$x_i$表示第i个物品是否放入背包，1表示放入，0表示不放入。那么问题的优化目标，使得价值最大化的数学表示形式为
$$\sum _{i=1}^n{v}_i{x}_i$$
这里有两个约束，一个是物品不能超过背包的最大容量，$x_i$是二值。即
$$\sum _{i=1}^n{w}_i{x}_i<=C$$以及
$$x_i\in 0,1,1<=i<=n$$
最优性原理是动态规划的基础，最优性原理是指多阶段决策过程中，无论初始状态和初始决策如何，对于前面决策所造成的某一个状态而言，其后各个阶段的决策序列必须构成最优策略。
设$V(i,wb)$为当前背包的剩余容量为wb，前i个物品最佳组合对应的价值
根据最优性原理，那么面对当前物品（即第i个物品）有两种可能性

1. 包的容量比该物品小，即物品大过包的容量，放不下了。此时背包里的价值和前i-1个的价值是一样的，即$V(i,wb)=V(i-1,wb)$
2. 包的剩余容量比该物品大，即还有空间放置该物品。但是装下该物品是否能达到当前最优价值呢？这就需要看装与不装之间的比较了。不装，$V(i,wb)=V(i-1,wb)$。装了，$V(i,wb)=V(i-1,wb-w_i)+v_i$,即背包容量减少了，但是价值增大了。此时需要取两种情况的最大值。
   由此可以得出递推关系式：

• 当$wb<w_i$时，不装，$V(i,wb)=V(i-1,wb)$
• 当$wb>=w_i$时， V ( i , w b ) = m a x { V ( i − 1 , w b ) , V ( i − 1 , w b − w i ) + v i } V(i,wb)=max\{V(i-1,wb), V(i-1,wb-w_{i})+v_{i} \} V(i,wb)=max{V(i−1,wb),V(i−1,wb−wi​)+vi​}

0-1背包示例

下面我们举例说明，设背包的容量为10，有5个物品可供装包，其质量和体积如下表。

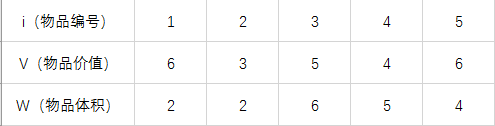
根据递推公式进行逐行填表，初始化表V(i,o) = 0，V(0,j) = 0,表的列维度从0到n，行维度从0到capacity。填表如下：

下面我们来分析一下这个表格：
表格的第一列0~5的数字，其中1 ~5是物品的编号。第一行0 ~ 10是背包的容量。除此以外的数字是物品组合的价值。下面一行一行的来分析。

1. 第0行元素都是零，即什么都不放的时候，背包价值为0
2. 第1行，当面对物品1时，物品1的价值为6，体积为2。此时第1行的第0列和第1列书包容量为0和1，不足以装下物品1，因此$V(i,wb)=V(i-1,wb)$被执行，即价值为0。第2列，容量为2，刚好装下物品1。如果装物品1，那么书包价值为6。不装则价值认为0。因此选择装，即执行 V ( i , w b ) = m a x { V ( i − 1 , w b ) , V ( i − 1 , w b − w i ) + v i } V(i,wb)=max\{V(i-1,wb), V(i-1,wb-w_{i})+v_{i} \} V(i,wb)=max{V(i−1,wb),V(i−1,wb−wi​)+vi​}。第3列，容量为3，也能装下物品1。执行 V ( i , w b ) = m a x { V ( i − 1 , w b ) , V ( i − 1 , w b − w i ) + v i } V(i,wb)=max\{V(i-1,wb), V(i-1,wb-w_{i})+v_{i} \} V(i,wb)=max{V(i−1,wb),V(i−1,wb−wi​)+vi​}，价值仍然是6。同理第4、5、6 、。。。10列也是一样。
3. 第2行，当面对物品2，物品2的价值为3，体积为2。此时第1行的第0列和第1列书包容量为0和1，不足以装下物品1和物品2。第2列，容量为2。此时我们需要求$V(2,2)$，即面对物品2，容量为2的情况下如何放物品。物品2的容量等于背包容量，即$wb>=w_i$成立，则 V ( i , w b ) = m a x { V ( i − 1 , w b ) , V ( i − 1 , w b − w i ) + v i } V(i,wb)=max\{V(i-1,wb), V(i-1,wb-w_{i})+v_{i} \} V(i,wb)=max{V(i−1,wb),V(i−1,wb−wi​)+vi​}将被执行，带入相应的数值，得到
   V ( 2 , 2 ) = m a x { V ( 1 , 2 ) , V ( 1 , 2 − 2 ) + 3 } V(2,2)=max\{V(1,2), V(1,2-2)+3 \} V(2,2)=max{V(1,2),V(1,2−2)+3}。由于$V(1,2)=6$，$V(1,2-2)+3=0+3$，则$V(2,2)=6$，在此框里填入6。当第3行时情况和第2行一样。当第4列时， V ( 2 , 4 ) = m a x { V ( 1 , 4 ) , V ( 1 , 4 − 2 ) + 3 } V(2,4)=max\{V(1,4), V(1,4-2)+3 \} V(2,4)=max{V(1,4),V(1,4−2)+3}，由于$V(1,4)=6$， $V(1,4-2)+3=6+3$，所以填入9。后面的列也是如此。
4. 第3行，当面对物品3，物品3的价值为5，体积为6。第1行的第0列和第1列和前面情况一样，$wb<w_i$时，填0。第2列，第3、4 、5列，$wb<w_i$时，同样执行$V(i,wb)=V(i-1,wb)$。直到第6列，$wb>=w_i$， V ( 3 , 6 ) = m a x { V ( 2 , 6 ) , V ( 2 , 6 − 6 ) + 5 } V(3,6)=max\{V(2,6), V(2,6-6)+5 \} V(3,6)=max{V(2,6),V(2,6−6)+5}，取6和5的最大值。第7列也如此。第8列， V ( 3 , 8 ) = m a x { V ( 2 , 8 ) , V ( 2 , 8 − 6 ) + 5 } V(3,8)=max\{V(2,8), V(2,8-6)+5 \} V(3,8)=max{V(2,8),V(2,8−6)+5}，取9和6+5之间的最大值。第10列， V ( 3 , 10 ) = m a x { V ( 2 , 10 ) , V ( 2 , 10 − 6 ) + 5 } V(3,10)=max\{V(2,10), V(2,10-6)+5 \} V(3,10)=max{V(2,10),V(2,10−6)+5}，取9和9+5之间的最大值。
5. 同理直到填满所有表格。

python代码实现

上述的推理过程用python来实现，代码如下：

# -*- coding: utf-8 -*-
# @Time    : 2019/12/3 15:22
# @Author  : HelloWorld！
# @FileName: bag.py
# @Software: PyCharm
# @Operating System: Windows 10
# @Python.version: 3.6

def zeroOneBig(num,capacity,weighList,valueList):
    valueExcel=[[0 for j in range(capacity+1)] for i in range(num+1)]
    print(valueExcel)
    for i in range(1,num+1):
        for j in range(1,capacity+1):
            valueExcel[i][j]=valueExcel[i-1][j]
            if j>=weighList[i-1] and valueExcel[i][j]<(valueExcel[i-1][j-weighList[i-1]]+valueList[i-1]):
                valueExcel[i][j]=valueExcel[i-1][j-weighList[i-1]]+valueList[i-1]
            for row in range(num+1):

                print(valueExcel[row])
            print('----------------------')
    return valueExcel
weight_list=[2,2,6,5,4]
value_list=[6,3,5,4,6]
valueExcel=zeroOneBig(5,10,weight_list,value_list)

输出的最后结果如下

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 6, 6, 6, 6, 6, 6, 6, 6, 6]
[0, 0, 6, 6, 9, 9, 9, 9, 9, 9, 9]
[0, 0, 6, 6, 9, 9, 9, 9, 11, 11, 14]
[0, 0, 6, 6, 9, 9, 9, 10, 11, 13, 14]
[0, 0, 6, 6, 9, 9, 12, 12, 15, 15, 15]
----------------------

由此可见，该问题的价值最大组合为15。该方法在时间复杂度上不能再优化了，但是在空间复杂度上还可以优化，即可以把上述的列表表示成一组。
代码如下：

def zeroOneOpt(num,capacity,weighList,valueList):
    valueRes=[0 for j in range(capacity+1)]

    for i in range(1,num+1):
        for j in range(capacity,0,-1):
            if j >weighList[i-1]:
                valueRes[j]=max(valueRes[j-weighList[i-1]]+valueList[i-1],valueRes[j])
        print('***********')
        print(valueRes)
    return valueRes
zeroOneOpt(5,10,weight_list,value_list)

结果如下：

***********
[0, 0, 0, 6, 6, 6, 6, 6, 6, 6, 6]
***********
[0, 0, 0, 6, 6, 9, 9, 9, 9, 9, 9]
***********
[0, 0, 0, 6, 6, 9, 9, 9, 9, 11, 11]
***********
[0, 0, 0, 6, 6, 9, 9, 9, 10, 11, 13]
***********
[0, 0, 0, 6, 6, 9, 9, 12, 12, 15, 15]

找到最佳组合

尽管已经找到最佳的价值总和是15，但是我们还不知道是哪几个物品的组合构成这个最优解。根据填表原理，$V(i,wb)=V(i-1,wb)$时，说明没有放置物品i，$V(i,wb)!=V(i-1,wb)$时，说明装了物品i，该物品是最优解的部分，此时由于$V(i,wb)= V(i-1,wb-w_{i})+v_{i} $，回到$V(i-1,wb-w_{i})$进一步寻找。重复直到遍历完所有物品。下面我们来分析表格，看看哪些个物品是最佳组合。

我们从最后一列，最后一行开始看。$V(5,10)!=V(4,10)$，因此物品5(体积为4，价值为6)是最佳组合之一。根据$V(i,wb)= V(i-1,wb-w_{i})+v_{i} $跳跃到$V(4,10-4)$。由于$V(4,6)=V(3,6)=9$，说明物品4没有被放入背包，不是最佳组合之一。下一步跳跃到V(3,6)，$V(3,6)=V(2,6)=9$，说明物品3也不是最佳组合之一。进入$V(2,6)$,$V(2,6)!=V(1,6)$，说明物品2是最佳组合。同理可得物品1也是最佳组合。即物品5,2，1是最佳组合。
实现代码如下：

def showRes(num,capacity,wightList,valueExcel):
    indexRes=[]
    j=capacity
    for i in range(num,0,-1):
        if valueExcel[i][j]!=valueExcel[i-1][j]:
            indexRes.append(i)
            j-=wightList[i-1]
    return indexRes
print(showRes(5,10,weight_list,valueExcel))

结果为[5, 2, 1]。

完全背包问题示例

根据0-1背包问题的递推公式，通过转换变化，得到完全背包问题的递推公式。
假设第i个物品放入背包的数量为k，而当前背包的容量为wb，那么k必须满足
$$0<=k<=wb//w_i$$
因此

• 当$0<=k<=wb//w_i$时， V ( i , w b ) = m a x { V ( i − 1 , w b ) , V ( i − 1 , w b − k ∗ w i ) + k ∗ v i } V(i,wb)=max\{V(i-1,wb), V(i-1,wb-k*w_{i})+k*v_{i} \} V(i,wb)=max{V(i−1,wb),V(i−1,wb−k∗wi​)+k∗vi​}
  python代码如下：

def compKnap(num,capacity,weightList,valueList):
    valueExcel = [[0 for j in range(capacity + 1)] for i in range(num + 1)]
    for i in range(1, num + 1):
        for j in range(1, capacity + 1):
            for k in range((j // weightList[i - 1]) + 1):
                if valueExcel[i][j] < (valueExcel[i - 1][j - k*weightList[i - 1]] + k*valueList[i - 1]):
                    valueExcel[i][j] = (valueExcel[i - 1][j - k * weightList[i - 1]] + k*valueList[i - 1])
    return valueExcel
print(compKnap(5,16,[5,4,7,2,6],[12,3,10,3,6]))

回溯法：

https://zhuanlan.zhihu.com/p/51015629
回溯法是一个既带有系统性又带有跳跃性的的搜索算法。它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时，总是先判断该结点是否肯定不包含问题的解。如果肯定不包含，则跳过对以该结点为根的子树的系统搜索，逐层向其祖先结点回溯。否则，进入该子树，继续按深度优先的策略进行搜索。回溯法在用来求问题的所有解时，要回溯到根，且根结点的所有子树都已被搜索遍才结束。而回溯法在用来求问题的任一解时，只要搜索到问题的一个解就可以结束。这种以深度优先的方式系统地搜索问题的解的算法称为回溯法，它适用于解一些组合数较大的问题。

0—1背包问题是一个子集选取问题，适合于用子集树表示0—1背包问题的解空间。在搜索解空间树是，只要其左儿子节点是一个可行结点，搜索就进入左子树，在右子树中有可能包含最优解是才进入右子树搜索。否则减去右子树。

为了便于计算上界，可先将物品依其单位重量价值从大到小排序，此后只要顺序考察各物品即可。在实现时，由MaxBoundary函数计算当前结点处的上界。它是类Knap的私有成员。Knap的其他成员记录了解空间树种的节点信息，以减少函数参数的传递以及递归调用时所需要的栈空间。在解空间树的当前扩展结点处，仅当要进入右子树时才计算上界函数MaxBoundary，以判断是否可以将右子树减去。进入左子树时不需要计算上界，因为其上界与父结点的上界相同。

当使用回溯法时，对于有N个物品的0-1背包问题，其解空间由长度为n的0-1向量组成，树的深度等于物品的个数。
如N=3时候，问题可以理解为：

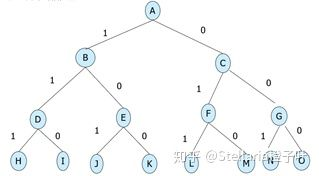
例如n=3, C=30, w={16, 15, 15}, v={45, 25, 25}。

参考文献：
https://blog.csdn.net/ggdhs/article/details/90648890