常见算法的分析与实现
分治算法
一、 基本思想
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。递归的求出子问题的解,并合并子问题的就可得到原问题的解。
二、分治法解题的一般步骤:
(1)分解,将要解决的问题划分成若干规模较小的同类问题;
(2)求解,当子问题划分得足够小时,用较简单的方法解决;
(3)合并,按原问题的要求,将子问题的解逐层合并构成原问题的解。
三、解决的问题:
二分搜索、合并排序、寻找中项和第k小元素、快速排序、大整数乘法、矩阵乘法
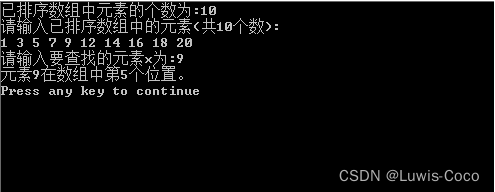
二分查找
算法描述:
将一个给定的元素x与一个已排序数组A[low···high]的中间元素做比较,如果x<A[mid],这里mid为(low+high)/2向下取整,则不考虑 A[low···high],而对A[low···mid-1] 重复实施相同的方法。类似地,如果 x>A[mid],则放弃 A[low···high],并对A[mid+1···high] 重复实施相同的方法。这就启示用递归算法BINARYSEARCHREC作为实现这一搜索的另一个方法。
算法 BINARYSEARCHREC
输入:按非降序排列的n个元素的数组A[1···n]和元素x 。
输出:如果x=A[j] ,则输出j ;否则输出 -1。
#include <stdio.h>
#define N 100
//子函数实现二分搜索算法,查找给定元素x的位置
int Binary_Search(int a[],int low,int high,int x)
{
int mid;
mid=(low+high)/2;
if(low>high)
return -1; /*查找失败*/
else if(x==a[mid])
return mid; /*找到元素的位置并返回*/
else if(x>a[mid])
return Binary_Search(a,mid+1,high,x);
else
return Binary_Search(a,low,mid-1,x);
}
//主函数
void main()
{
int a[N];
int i,t,x,n;
printf("请输入已排序数组中元素的个数n:");
scanf("%d",&n);
printf("请输入已排序数组中的元素(共%d个数):\n",n);
for(i=0;i<n;i++)
scanf("%d",&a[i]); /*从键盘输入一组数*/
printf("请输入要查找的元素x为:");
scanf("%d",&x);
t=Binary_Search(a,0,n-1,x); /*调用子函数,查找元素x在数组a[n]中的位置*/
printf("元素x在数组中第%d个位置。\n",t+1); /*因为数组的下标从0开始,实际的位置应为其坐标位置加1*/
}
测试结果
合并排序
算法描述:
合并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
合并排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
#include<stdio.h>
#include<stdlib.h>
//将两个有序的数组R[low...m]和R[m+1...high]归并成一个有序的数组R[low..high]
void Merge(int R[],int b[],int low,int m,int high)
{
int i=low,j=m+1,p=0;
while(i<=m&&j<=high) /*两子数组非空时取其小者输出到R1[p]上*/
b[p++]=(R[i]<=R[j])?R[i++]:R[j++];
while(i<=m) /*若第1个子文件非空,则复制剩余记录到R1中*/
b[p++]=R[i++];
while(j<=high) /*若第2个子文件非空,则复制剩余记录到R1中*/
b[p++]=R[j++];
for(p=0,i=low;i<=high;p++,i++)
R[i]=b[p]; /*归并完成后将结果复制回R[low..high]*/
}
//用分治法对R[low..high]进行二路归并排序
void MergeSort(int R[],int low,int high)
{
int mid;
int b[8];
if(low<high) /*区间长度大于1*/
{
mid=(low+high)/2; /*分解*/
MergeSort(R,low,mid); /*递归地对R[low..mid]排序*/
MergeSort(R,mid+1,high); /*递归地对R[mid+1..high]排序*/
Merge(R,b,low,mid,high); /*组合,将两个有序区归并为一个有序区*/
}
}
void main()
{
int a[8];
int i,j;
for(j=0;j<8;j++)
a[j]=rand()%100; /*系统随机生成8个数*/
//*scanf("%d",&array[j]);取消此注释语句可以手动输入无序数组
printf("随机生成数组为:\n");
for(i=0;i<8;i++)
printf("%d ",a[i]);
MergeSort(a,0,7);
printf("\n已排序数组为:\n");
for(i=0;i<8;i++)
printf("%d ",a[i]);
printf("\n\n");
}
寻找中项和第k小元素
n个已经排序的A[1···n]序列的中项是其“中间”元素。如果 n 是奇数,则中间元素是序列中第(n+1)/2个元素;如果n是偶数,则存在两个中间元素,所处的位置分别是n/2和n/2+1,在这种情况下,我们将选择第n/2个最小元素。这样,综合两种情况,中项是第 ceil(n/2)最小元素。
寻找中项的一个直接的方法是对所有的元素排序并取出中间一个元素,这个方法需要O(nlogn)时间,因为任何基于比较的排序过程在最坏的情况下必须至少要花费这么多时间。
#include <stdio.h>//必须添加的头文件
#include <stdlib.h>//为了使用rand()函数而加的头文件
//本程序用到了“改进的快速排序”的算法思想,但最终输出的序列并不一定是有序的
void exchange(int array[],int i,int j)
{
int temp;
temp=array[i];
array[i]=array[j];
array[j]=temp;
}
int partition(int array[],int p,int r)
{
int x,i,j;
x=array[r];
i=p-1;
for(j=p;j<r;j++)
{
if(array[j]<=x)/*<=i位置上的数都比x小;>=j位置上的数都比x大;*/
{
i++;
exchange(array,i,j);
}
}
exchange(array,i+1,r);
return i+1;
}
int Randomized_partition(int array[],int p,int r)
{
int i;
i=p+rand()%(r-p);
exchange(array,i,r);
return partition(array,p,r);
}
int Randomized_select(int array[],int p,int r,int i)/*获得第i小的数*/
{
int q,k;
if(p==r)
return array[p];
q=Randomized_partition(array,p,r);//获得中轴上的值
k=q-p+1;//记录的是第几个位置,并不是下标值
if(i==k)
return array[q];
else if(i<k)
return Randomized_select(array,p,q-1,i);
else
return Randomized_select(array,q+1,r,i-k);
}
void main()
{
int array[10];
int i,j,n,t;
while(1)
{
printf("输入第i小个数:");
scanf("%d",&n);
for(j=0;j<10;j++)
array[j]=rand()%100;//查询随机的一组数
//scanf("%d",&array[j]);//查询从键盘输入的一组数
t=Randomized_select(array,0,9,n);
printf("第%d小的数为:%d\n",n,t);
for(i=0;i<10;i++)//最终输出的序列并不一定是有序的
printf("数列:%d\n",array[i]);
}
}
测试结果
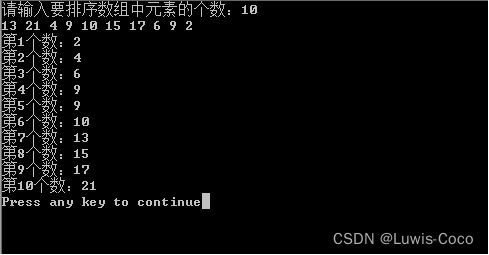
快速排序
高效的排序算法:QUICKSORT。该排序算法具有O(nlogn)的平均运行时间,这个算法优于MERGESORT的一点是它在原位上排序,即对于被排序的元素,不需要辅助的存储空间。在描述这个排序算法之前,需要以下的划分算法,它是算法QUICKSORT的基础。
算法QUICKSORT在它的最简单的形式中能概括如下,要排序的元素A[low···high] 通过算法SPLIT重新排列元素,使得原先在A[low]中的主元占据其正确的位置A[w] ,并且所有小于或等于A[w] 的元素所处的位置为 A[low···w-1],而所有大于A[w] 的元素所处的位置是 A[w+1···high]。子数组A[low···w-1] 和 A[w+1···high]递归地排序,产生整个排序数组。算法SPLIT和算法QUICKSORT的关系类似于算法MERGE和算法MERGESORT的关系,两个排序算法都由对名为SPLIT和MERGE的算法之一的一系列调用组成。然而,从算法观点而言,两者之间存在着细微的差别:在算法MERGESORT中,合并排序序列属于组合步骤,而在算法QUICKSORT中的划分过程则属于划分步骤。事实上,在算法QUICKSORT中组合步骤是不存在的。
#include <stdio.h>
#include <stdlib.h>
#define N 99
void QuickSort(int a[],int l,int r)
{
int temp;
int i=l,j=r;
temp=a[l]; /*将数组中的第一个元素作为中轴*/
if(l<r) /*所有递归过程完成的条件控制*/
{
while(i!=j)
{/*一次递归完成的条件控制*/
while(j>i&&a[j]>temp) --j; /*从右往左扫描找到一个小于temp的元素*/
if(i<j)
{
a[i]=a[j]; /*找到一个小于temp的元素放在a[i]处*/
i++;
}
while(i<j&&a[i]<temp) ++i; /*从左往右扫描找到一个大于temp的元素*/
if(i<j)
{
a[j]=a[i]; /*找到一个大于temp的元素放在a[j]处*/
--j;
}
}
a[i]=temp;
QuickSort(a,l,i-1);
QuickSort(a,i+1,r);
}
}
void main()
{
int a[N];
int i,j,n;
printf("请输入要排序数组中元素的个数:");
scanf("%d",&n);
for(i=0;i<n;i++)
//a[i]=rand()%100;此语句可以使系统随机生成n个数
scanf("%d",&a[i]);/*从键盘输入一组数*/
QuickSort(a,0,n-1);
for(j=0;j<n;j++)
printf("第%d个数:%d\n",j+1,a[j]);
}
测试结果
动态规划
一、基本思想
基本思想与分治法类似,也是将待求解的问题分解为若干个子问题(阶段),按顺序求解子阶段,前一子问题的解,为后一子问题的求解提供了有用的信息。在求解任一子问题时,列出各种可能的局部解,通过决策保留那些有可能达到最优的局部解,丢弃其他局部解。依次解决各子问题,最后一个子问题就是初始问题的解。
二、动态规划基本步骤:
(1)找出最优解的性质,并刻画其结构特征。
(2)递归地定义最优值。
(3)以自底向上的方式计算出最优值。
(4)根据计算最优值时得到的信息,构造最优解
三、解决的问题
矩阵链相乘、最长公共子序列问题、背包问题
最长公共子序列
问题描述:
在字母表Σ上,分别给出两个长度为n和m的字符串A和B,确定在A和B中最长公共子序列的长度。这里,A=a1 a2⋯an的子序列是一个形式为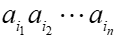 的字符串,其中每个i,j都在1和n之间,并且
的字符串,其中每个i,j都在1和n之间,并且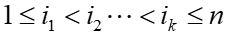 。例如,如果Σ={x,y,z},A=zxyxyz和B=xyyzx,那么xyy同时是A和B的长度为3的子序列。然而,他不是A和B的最长公共子序列,因为字符串xyyz也是A和B的公共的子序列,由于这两个字符串没有比4更长的公共子序列,因此,A和B的最长公共子序列的长度为4。
。例如,如果Σ={x,y,z},A=zxyxyz和B=xyyzx,那么xyy同时是A和B的长度为3的子序列。然而,他不是A和B的最长公共子序列,因为字符串xyyz也是A和B的公共的子序列,由于这两个字符串没有比4更长的公共子序列,因此,A和B的最长公共子序列的长度为4。
算法描述:
为了使用动态规划技术,我们首先寻找一个求最长公共子序列长度的递推式,令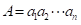 和
和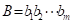 ,令L[i][j]表示
,令L[i][j]表示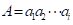 和
和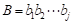 的最长公共子序列的长度。注意,i和j可能是0,此时,
的最长公共子序列的长度。注意,i和j可能是0,此时,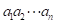 和
和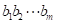 中的一个或同时可能为空字符串。即如果i=0或j=0,那么L[i][j]=0。有此得算法的递推式:
中的一个或同时可能为空字符串。即如果i=0或j=0,那么L[i][j]=0。有此得算法的递推式:
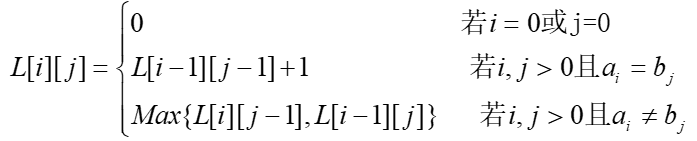
算法分析:最长公共子序列的时间复杂度是O(mn),空间复杂度是 O(mn)。
#include<stdio.h>
#include<string.h>
#define N 50
void LCSLength(char x[N+1],char y[N+1],int B[N+1][N+1]);
void LCS(int i,int j,char x[N+1],int B[N+1][N+1]);
void main()
{
char x[N+1],y[N+1];int B[N+1][N+1];int lx,ly;
printf("请输入序列X的元素(按回车键结束输入):\n");
scanf("%s",x+1); /*从x[1]开始输入数据*/
printf("请输入序列Y的元素(按回车键结束输入):\n");
scanf("%s",y+1); /*从y[1]开始输入数据*/
lx=strlen(x+1);
ly=strlen(y+1);
printf("LCS的最长公共子序列的长度是: ");
LCSLength(x,y,B);
printf("\n");
printf("LCS的最长公共子序列是: ");
LCS(lx,ly,x,B);
printf("\n\n");
}
void LCSLength(char x[],char y[],int B[N+1][N+1])
{
int i,j,m,n;
int C[N+1][N+1]; /*C[i][j]表示记录序列{x1,x2,……xi}与序列{y1,y2,……yj}的最长公共子序列元素的个数*/
m=strlen(x+1);
n=strlen(y+1);
for(i=1;i<=m;i++)
C[i][0]=0;
for(j=1;j<=n;j++)
C[0][j]=0;
for(i=1;i<=m;i++)
for(j=1;j<=n;j++)
{
if(x[i]==y[j])
{
C[i][j]=C[i-1][j-1]+1;
B[i][j]=1;
}
else if(C[i][j-1]>C[i-1][j])
{
C[i][j]=C[i][j-1];
B[i][j]=2;
}
else
{
C[i][j]=C[i-1][j];
B[i][j]=3;
}
}
printf("%d",C[m][n]);
}
void LCS(int i,int j,char x[],int B[N+1][N+1])
{
if(i==0||j==0) return;
if(B[i][j]==1)
{
LCS(i-1,j-1,x,B);
printf("%c",x[i]);
}
else if(B[i][j]==2)
{
LCS(i,j-1,x,B);
}
else
{
LCS(i-1,j,x,B);
}
}
测试结果
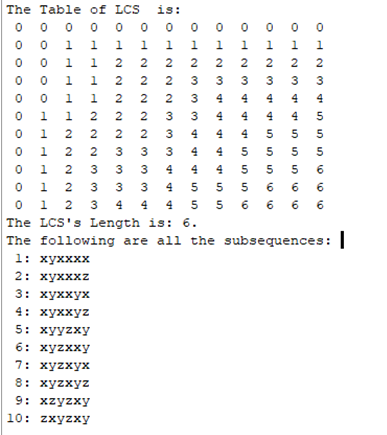
求所有最长公共子序列
import java.util.Arrays;
public class LongestCommonSubsequence{
public static String[] tempLCS = new String[200];// 用于暂存程序初步找到的所有最长公共子序列,包括重复的子序列在内
public static int index = 0;
// 其作用有两个:
// 一个是作为字符串数组 tempLCS 的游标;
// 另一个是作为函数 Arrays.copyOfRange(original, from, to) 的第三个参数。
/**
* 根据规则,填充最长子序列表格
*
* @param charArray1
* @param charArray2
* @return
*/
public static int[][] makeLCSTable(char[] charArray1, char[] charArray2) {
int[][] tableLCS = new int[charArray1.length + 1][charArray2.length + 1];
for (int i = 0; i < tableLCS.length; i++) {
for (int j = 0; j < tableLCS[i].length; j++) {
if (i == 0 || j == 0) {
tableLCS[i][j] = 0;
} else {
if (charArray1[i - 1] == charArray2[j - 1]) {
tableLCS[i][j] = tableLCS[i - 1][j - 1] + 1;
} else {
tableLCS[i][j] = Math.max(tableLCS[i][j - 1], tableLCS[i - 1][j]);
}
}
}
}
for (int p = 0; p < tableLCS.length; p++) {// 输出表格
for (int q = 0; q < tableLCS[p].length; q++) {
if (q == (tableLCS[p].length - 1)) {
System.out.printf("%3s", tableLCS[p][q] + " ");
System.out.println();
} else {
System.out.printf("%3s", tableLCS[p][q] + " ");
}
}
}
return tableLCS;// 返回最长公共子序列的长度
}
/**
* 根据表格找到所有的最长子序列
*
* @param charArray1
* 第一个字符串
* @param charArray2
* 第二个字符串
* @param tableLCS
* 最长子序列 表格
* @param length1
* 第一个字符串的长度
* @param length2
* 第二个字符串的长度
* @param stringBuff
* 将找到的每一个公共元素暂存下来,之后输出到 tempLCS[m++] 中,作用类似于栈
*/
public static void searchSubString(char[] charArray1, char[] charArray2, int[][] tableLCS, int length1, int length2,
StringBuffer stringBuff) {
StringBuffer stringBuff2 = new StringBuffer();
for (int i = length1, j = length2; i != 0 && j != 0;) {
if (charArray1[i - 1] == charArray2[j - 1]) {
stringBuff.append(charArray1[i - 1]);//向字符串缓冲区"追加"元素
i--;
j--;// 移动到对角元素继续寻找下一个公共元素
} else {
if (tableLCS[i - 1][j] == tableLCS[i][j]) {// 移动到上一行同一列(上面)元素处继续找
stringBuff2 = new StringBuffer(stringBuff);// 暂存当前已找到的公共子序列,便于递归返回之后恢复
searchSubString(charArray1, charArray2, tableLCS, --i, j, stringBuff);
stringBuff = stringBuff2;// 递归结束后恢复已找到的公共子序列,便于换方向继续找
i++; // 前一次寻找时减了一次,再次寻找时再加回来
}
if (tableLCS[i][j - 1] == tableLCS[i][j]) {// 移动到前一列同一行(左面)元素处继续找
stringBuff2 = new StringBuffer(stringBuff);
searchSubString(charArray1, charArray2, tableLCS, i, --j, stringBuff);
stringBuff = stringBuff2;
j++;
}
return;
}
}
// for (int j = 0; j <= m; j++) {
// if ((stringBuff.reverse()).toString().equals(deleteRepeat[j]))
// index = false;
// break;
// }
//
// if (index) {
tempLCS[index++] = (stringBuff.reverse()).toString();
// }
}
/**
* 将给定已排序的字符串数组中,不相同的元素集中存储到最前面,之后返回这些不相同元素组成数组的长度
*
* @param strArray
* @return
*/
public static int removeDuplicates(String[] strArray) {
if (strArray.length < 1)
return strArray.length;
int slow = 1;
for (int fast = 1; fast < strArray.length; fast++) {
if (strArray[fast] == null) {
break;
} else {
if (strArray[fast].equals(strArray[slow - 1])) {
continue;
} else {
strArray[slow++] = strArray[fast];
}
}
}
return slow;
}
/**
* 将函数 makeLCSTable()、pringSubString() 和 removeDuplicates() 函数集中一次运行
* @param str1
* @param str2
*/
public static void findLCS(String str1, String str2) {
char[] charArray1 = str1.toCharArray();
char[] charArray2 = str2.toCharArray();
System.out.println("The Table of LCS is: ");
int[][] tableLCS = makeLCSTable(charArray1, charArray2);
System.out.println("The LCS's Length is: " + tableLCS[str1.length()][str2.length()] + ".");
StringBuffer stringBuff = new StringBuffer();
searchSubString(charArray1, charArray2, tableLCS, charArray1.length, charArray2.length, stringBuff);// 输出最长公共子序列
// 生成包含所有最长公共子序列的字符串数组 tempLCS[]
System.out.println("The following are all the subsequences: ");
String[] resultsLCS = Arrays.copyOfRange(tempLCS, 0, index);
// 存储最终所有的最长公共子序列,不包括重复的子序列
// 截取字符数组 tempLCS 中从第 0 个数组元素(包括 tempLCS[0])到第 index 个数组元素(不包括 tempLCS[index]),并赋值给 resultLCS 字符数组。
Arrays.sort(resultsLCS); // 将字符数组个元素按照ASCII编码的顺序升序排列
int endNum = removeDuplicates(resultsLCS); // resultsLCS[] 字符串数组去重
for (int i = 0; i < endNum; i++) {
System.out.printf("%2d", (i + 1));// 规定数字都按占两位格式整齐输出,防止输出到后面出现混乱
System.out.println(": " + resultsLCS[i]);
}
}
public static void main(String[] args) {
String A = "xyxxzxyzxy";
String B = "zxzyyzxxyxxz";
findLCS(A, B);
}
}
测试结果
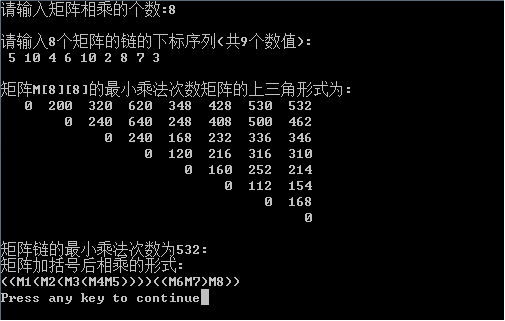
矩阵链相乘
问题描述:用动态规划算法找出使n个矩阵乘法次数最小的顺序。
算法描述:对于给定的矩阵链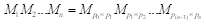 ,由于对于每个i,1≤i≤n矩阵Mi的列数一定等于矩阵M(i+1)的行数,因此指定每个矩阵的行数和最右面矩阵的列数就够了。这样就假设我们有n+1维数
,由于对于每个i,1≤i≤n矩阵Mi的列数一定等于矩阵M(i+1)的行数,因此指定每个矩阵的行数和最右面矩阵的列数就够了。这样就假设我们有n+1维数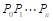 ,这里P(i-1)和Pi分别是矩阵Mi中的行数和列数。以后,我们将用M(i,j)来记Mi M(i+1)⋯Mj的乘积,我们还将假设链M(i,j)的最小乘法次数记为M[i][j]。对于给定的一对索引i和j,1≤i<j≤n,M(i,j)可用如下方法计算。设k是i+1和j之间的一个索引,计算两个矩阵
,这里P(i-1)和Pi分别是矩阵Mi中的行数和列数。以后,我们将用M(i,j)来记Mi M(i+1)⋯Mj的乘积,我们还将假设链M(i,j)的最小乘法次数记为M[i][j]。对于给定的一对索引i和j,1≤i<j≤n,M(i,j)可用如下方法计算。设k是i+1和j之间的一个索引,计算两个矩阵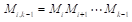 和
和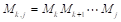 ,那么M(i,j)=M(i,k-1) M(k,j)。M(i,j)的最小乘法次数是计算M(i,k-1)的最小乘法次数加上的M(k,j)再加上M(i,k-1)乘上M(k,j)的乘法次数。这导致了以下找出k值的公式,其中的k使执行矩阵乘法所需要的乘法次数最小。算法的递推式:
,那么M(i,j)=M(i,k-1) M(k,j)。M(i,j)的最小乘法次数是计算M(i,k-1)的最小乘法次数加上的M(k,j)再加上M(i,k-1)乘上M(k,j)的乘法次数。这导致了以下找出k值的公式,其中的k使执行矩阵乘法所需要的乘法次数最小。算法的递推式:
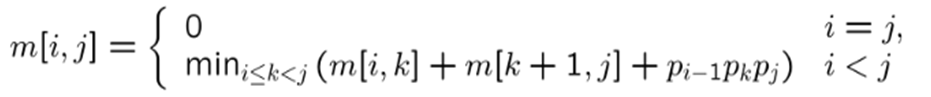 算法分析:矩阵链相乘的时间复杂度是Θ(n3),算法所需要的工作空间取决于所需要的三角数组的大小,也就是其空间复杂度是Ω(n2)。
算法分析:矩阵链相乘的时间复杂度是Θ(n3),算法所需要的工作空间取决于所需要的三角数组的大小,也就是其空间复杂度是Ω(n2)。
#include<iostream.h>
#define N 100 //数组的阶乘最多为100
#define inifity 32767 //int的取值范围是-32768~32767
void Mathxchain(int P[N],int n);
void Traceback(int s[N][N],int i,int j);
void main()
{
int n,i; /*n记录矩阵的个数*/
int P[N]; /*P[N],记录n个矩阵的下标序列*/
printf("请输入矩阵相乘的个数:");
scanf("%d",&n);
printf("\n请输入%d个矩阵的链的下标序列(共%d个数值):\n",n,n+1);
for(i=0;i<=n;i++) /*输入矩阵的下标序列*/
{
scanf("%d",&P[i]);
}
Mathxchain(P,n);
}
/*子函数Mathxchain(int ,int )计算从第i个矩阵到第j个矩阵的最小乘法次数*/
void Mathxchain(int P[N],int n)
{ int i,j,l,k,q;
int M[N][N]; /*将第i个矩阵到第j个矩阵的最小乘法次数存放至M[][]的上三角矩阵中*/
int s[N][N];
for(i=1;i<=n;i++) /*单个矩阵的最小乘法次数为0*/
{
M[i][i]=0;
}
for(l=2;l<=n;l++) /*将第i个矩阵到第j个矩阵的最小乘法次数存放至M[][]的上三角矩阵中*/
{
for(i=1;i<=n-l+1;i++)
{
j=i+l-1;
M[i][j]=inifity;
for(k=i;k<=j-1;k++)
{
q=M[i][k]+M[k+1][j]+P[i-1]*P[k]*P[j];
if(q<M[i][j])
{
M[i][j]=q;
s[i][j]=k;
}
}
}
}
printf("\n M[%d][%d]的矩阵的上三角形式为:\n",n,n);
for(i=1;i<=n;i++)
{ for(k=1;k<i;k++) printf(" ");
for(j=i;j<=n;j++)
{ printf("%4d ",M[i][j]);}
printf("\n");
}
printf("\n矩阵链的最小乘法次数为%d:\n",M[1][n]);
printf("矩阵加括号后相乘的形式:\n");
Traceback(s,1,n);
printf("\n");
}
void Traceback(int s[N][N],int i,int j)
{
if(i==j)
{printf("M%d",i);}
else if(i+1==j)
{
printf("(M%dM%d)",i,j);
}
else
{
printf("(");
Traceback(s,i,s[i][j]);
Traceback(s,s[i][j]+1,j);
printf(")");
}
}
测试结果
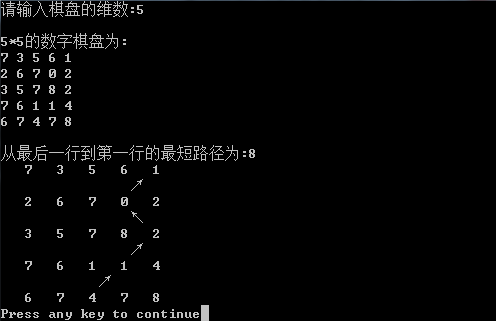
数字棋盘
问题描述:
在n×n的数字棋盘中,每个方格有一个数字成本C[i][j],求从最后一行开始到第一行的最短路径(所有路过的成本方格和最小),假定每次只能允许沿 ↖,↑,↗移动。算法的递推式:
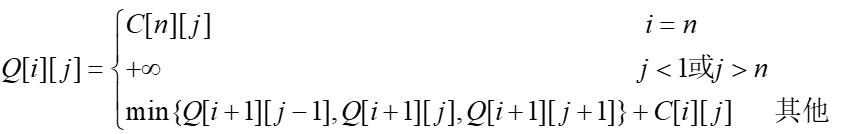
其中Q[i][j]表示从最后一行开始走到[i][j]位置的最小权值 。
算法分析:数字棋盘的时间复杂度是Θ(n2),算法所需要的工作空间取决于所需要的三角数组的大小,也就是其空间复杂度是Ω(n2)。
//#include<stdio.h>
//#include<stdlib.h>
#include<stdio.h>
#define N 99
#define infinity 32767
int c[N+1][N+1],p[N+1][N+1],q[N+1][N+1];
int n;
#define min(a,b) a>b?b:a
void CompleteQPAarray(); //构造P矩阵和Q矩阵。
void PrintPath(int i,int j);
void ShortestPath();
void main()
{
int i,j;
printf("请输入棋盘的维数:");
scanf("%d",&n);
printf("\n%d*%d的数字棋盘为:\n",n,n);
for(i=1;i<=n;i++)
{ for(j=1;j<=n;j++)
scanf("%d",&c[i][j]);
}
printf("\n从最后一行到第一行的最短路径为:");
CompleteQPAarray();
printf("\n");
}
void CompleteQPAarray()
{
int i,j,m;
for(j=1;j<=n;j++)
q[n][j]=c[n][j];
for(i=1;i<=n;i++)
{
q[i][0]=infinity;
q[i][n+1]=infinity;
}
for(i=n-1;i>=1;i--)
for(j=1;j<=n;j++)
{
m=min(q[i+1][j-1],q[i+1][j]);
m=min(m,q[i+1][j+1]);
q[i][j]=m+c[i][j];
if(m==q[i+1][j-1])
p[i][j]=-1;
else if(m==q[i+1][j])
{
p[i][j]=0;
}
else
p[i][j]=1;
}
ShortestPath();
}
void ShortestPath()
{
int min,k,j;
min=q[1][1];
k=1;
for(j=2;j<=n;j++)
{
if(q[1][j]<min)
{
min=q[1][j];
k=j;
}
}
printf("%d\n",q[1][n]);
PrintPath(1,k);
}
void PrintPath(int i,int j)
{
int k;
for(k=1;k<=n;k++)
printf("%4d",c[i][k]);
printf("\n");
if(p[i][j]==-1)
{
for(k=1;k<j-1;k++)
printf(" ");
printf(" ↗\n");
}
else if(p[i][j]==0)
{
for(k=1;k<j;k++)
printf(" ");
printf(" ↑\n");
}
else
{
for(k=1;k<j+1;k++)
printf(" ");
printf("↖\n");
}
if(i==n-1)
{
for(k=1;k<=n;k++)
printf("%4d",c[i+1][k]);
}
else
PrintPath(i+1,j+p[i][j]);
}
测试结果
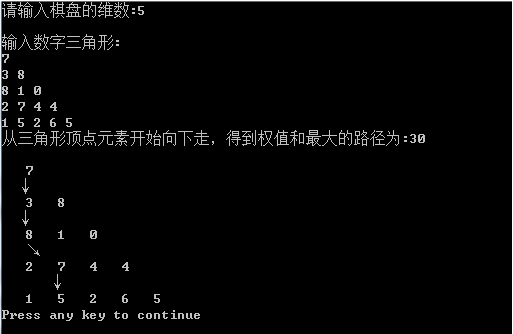
数字三角形
问题描述:给定n行的数字三角形(每个元素为小于100的正整数),找出从顶点到最后一行的权值之和最大的路径,假设每次只能沿↙、↘向下走一行。例:
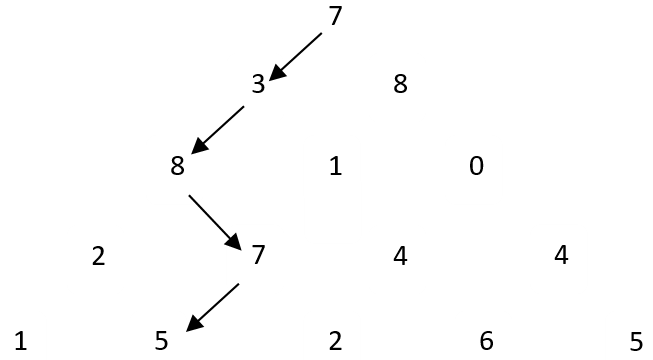
算法描述:数字三角形在计算机中的存储结构为:
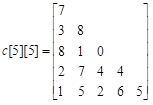
定义二维数组q[N+1][N+1],q[i][j]记录从第一个元素到第i行第j个元素权值的最大值。有数字三角形每次只能沿↙、↘向下走一行,再联系数字三角形在计算机中的存储结构,每个元素只能沿↓或↘向下走一行。定义二维数组p[N+1][N+1],p[i][j]=-1,说明上一个元素是在矩阵中沿↓到达元素c[i][j]的,p[i][j]=0,说明上一个元素是在矩阵中沿↘到达元素c[i][j]的。算法的递推式如下
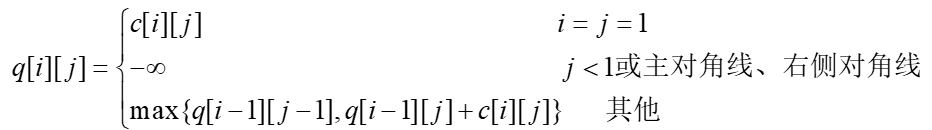
算法分析:数字三角形的时间复杂度是Θ(n2),算法所需要的工作空间取决于所需要的三角数组的大小,也就是其空间复杂度是Ω(n2)。
#include<stdio.h>
#include<stdlib.h>
#define N 99
#define maxnum -32767
int n;
int X[N+1],Y[N+1]; /*数组X[]存放最大权值路径上的数值,数组Y[]存放最大权值路径上的树值的纵坐标*/
int c[N+1][N+1],p[N+1][N+1],q[N+1][N+1];
void CompleteQPAarray();/*构造P矩阵和Q矩阵*/
void PrintPath();
void ShortestPath();
void main()
{
int i,j;
printf("请输入棋盘的维数:");
scanf("%d",&n);
printf("\n输入数字三角形:\n");
for(i=1;i<=n;i++)
{ for(j=1;j<=i;j++)
scanf("%d",&c[i][j]);
}
CompleteQPAarray();
printf("\n");
}
void CompleteQPAarray()
{
int i,j,m;
q[1][1]=c[1][1];
for(i=1;i<=n;i++)
{
q[i][0]=maxnum;
q[i][i+1]=maxnum;
}
for(i=2;i<=n;i++)
for(j=1;j<=i;j++)
{
m=max(q[i-1][j-1],q[i-1][j]);
q[i][j]=m+c[i][j];
if(m==q[i-1][j-1])
p[i][j]=-1;
else
p[i][j]=0;
}
ShortestPath();
}
void ShortestPath()
{
int i,j,k,max;
max=q[n][1];
k=1;
for(j=2;j<=n;j++)
{
if(q[n][j]>max)
{
max=q[n][j];
k=j;
}
}
for(i=n;i>=1;i--)
{
Y[i]=k;
X[i]=c[i][k];
k=k+p[i][k];
}
printf("从三角形顶点元素开始向下走,得到权值和最大的路径为:%d\n\n",max);
PrintPath();
}
void PrintPath()
{
int i,j,k;
for(i=1;i<=n;i++)
{
for(k=1;k<=i;k++)
printf("%4d",c[i][k]);
printf("\n");
j=Y[i+1];
if(p[i+1][j]==0)
{
for(k=1;k<Y[i];k++)
printf(" ");
printf(" ↓\n");
}
else
{
for(k=1;k<Y[i];k++)
printf(" ");
printf(" ↘\n");
}
if(i==n-1)
{
for(k=1;k<=i+1;k++)
printf("%4d",c[n][k]);
break;
}
}
}
测试结果
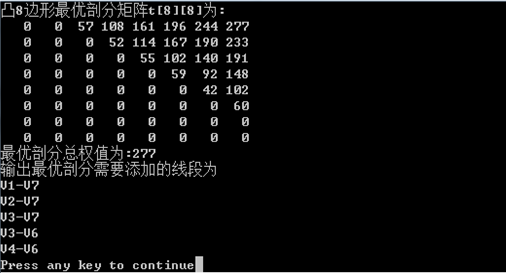
凸多边形最优三角剖分
问题描述:
给定n个顶点的凸多边形,知道任意一对顶点构成的边的权值,添加n-3边将凸多边形剖分成n-2个三角形,使得这些三角形的边的权值之和最小。
算法描述:
矩阵t[i][j]表示连续顶点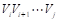 围成的凸多边形的最优剖分。t[i][j]是对称矩阵,只填写上三角形。因为一个点和两个点都不能组成三角形,所以第一条对角线和第二条对角线上的元素均为0,即t[i][i]=0,t[i][i+1]=0。从第三条对角线开始填写,t[0][n-1]即是对n顶点凸多边形最优剖分的权值。
围成的凸多边形的最优剖分。t[i][j]是对称矩阵,只填写上三角形。因为一个点和两个点都不能组成三角形,所以第一条对角线和第二条对角线上的元素均为0,即t[i][i]=0,t[i][i+1]=0。从第三条对角线开始填写,t[0][n-1]即是对n顶点凸多边形最优剖分的权值。
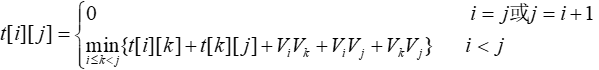
算法分析:凸多边形最优剖分的时间复杂度是Θ(n3),算法所需要的工作空间取决于所要剖分的凸多边形的大小,也就是其空间复杂度是Ω(n2)。
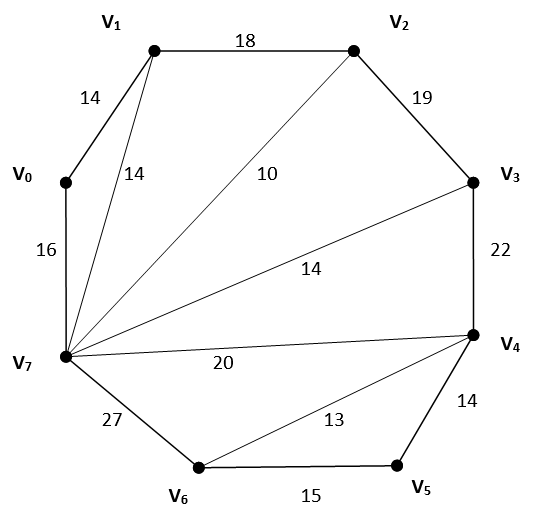
#include <stdio.h>
#include <string.h>
#define N 8 //凸N边形,v0,v1,......,v(N-1)
#define infinity 32767 //int的取值为 -32768~ 32767
int graph[N][N]=
{
0, 14, 25, 27, 10, 11, 24, 16,
14, 0, 18, 15, 27, 28, 16, 14,
25, 18, 0, 19, 14, 19, 16, 10,
27, 15, 19, 0, 22, 23, 15, 14,
10, 27, 14, 22, 0, 14, 13, 20,
11, 28, 19, 23, 14, 0, 15, 18,
24, 16, 16, 15, 13, 15, 0, 27,
16, 14, 10, 14, 20, 18, 27, 0
};
int t[N][N];
int s[N][N];
int w(int m, int n, int p)
{
return graph[m][n] + graph[m][p] + graph[n][p];
}
void sp(int m,int n)//输出最优剖分需要添加的线段,表示多边形V_{m-1},......, V_n 的划分
{
if (n-m<=2)// 只剩一个三角形了,即最后只剩两个相邻的边了,不再划分
return ;
else if(s[m][n]-m>=2)// 左边还需划分
{
printf("V%d-V%d\n", m, s[m][n]);
sp(m, s[m][n]);
}
if (n-s[m][n]>=2)// 右边还需划分
{
printf("V%d-V%d\n", s[m][n], n);
sp(s[m][n], n);
}
}
int main()
{
int i, j, k, r, u;
memset(t, 0, sizeof(t)); //将二维数组t[][]的元素全置为0
memset(s, 0, sizeof(s));
for (r=3; r<=N; r++) //从第3斜对角线至右上角
for (i=0; i<=N-r; i++) //每个对角线中的元素个数
{
j = i + r-1; //列坐标
t[i][j]=infinity;
for (k=i+1; k<j; k++)
{
u = t[i][k] + t[k][j] + w(i, k, j);
if (u<t[i][j])
{
t[i][j] = u;
s[i][j] = k;
}
}
}
printf("凸%d边形最优剖分矩阵t[%d][%d]为:\n",N,N,N);
for(i=0;i<N;i++)
{
for(j=0;j<N;j++)
printf("%4d",t[i][j]);
printf("\n");
}
printf("最优剖分总权值为:%d\n",t[0][N-1]);
printf("输出最优剖分需要添加的线段为\n");
sp(0,N-1);
return 0;
}
测试结果
所有点对的最短路径问题
问题描述:
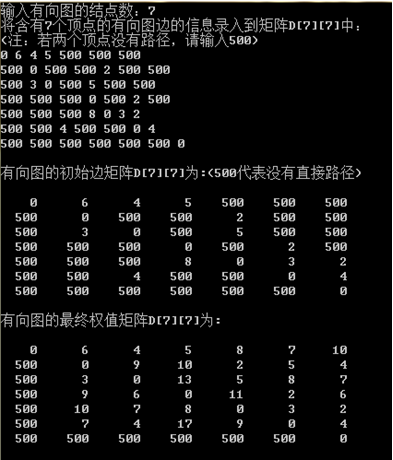
设G=(V,E)是一个有向图,其中的每条边(i,j)有一个非负的长度权值w[i][j],如果从顶点i到顶点j没有边,则w[i][j]=∞(输入时在矩阵中用500表示)。问题是要找出从每个顶点到其他所有顶点的最短路径长度。
实验数据:
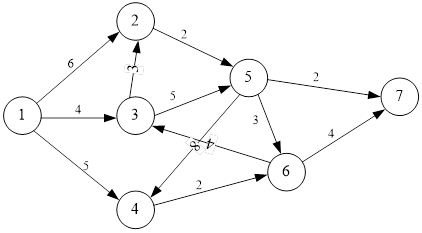
用1个n×n维p矩阵用来记录路径。n+1个n×n维矩阵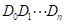 ,如果i≠j且(i,j)是G中的边,置D0[i][j]=0,D0[i][j]=w[i][j],否则置D0[i][j]=∞;设i和j是V中两个不同的顶点,定义Dk[i][j]是从i到j,并且不经过{k+1,k+2,⋯,n} (n是有向图中的顶点个数)中任何结点的最短路径的长度,即:
,如果i≠j且(i,j)是G中的边,置D0[i][j]=0,D0[i][j]=w[i][j],否则置D0[i][j]=∞;设i和j是V中两个不同的顶点,定义Dk[i][j]是从i到j,并且不经过{k+1,k+2,⋯,n} (n是有向图中的顶点个数)中任何结点的最短路径的长度,即:![D_k [i][j]=min{ D_(k-1) [i][j],D_(k-1) [i][k]+D_(k-1) [k][j]}](https://img-blog.csdnimg.cn/3f521723eb304633bfdbf134e2b1e3cf.png) 。
。
# include<iostream.h>
# include<stdio.h>
# include <iomanip.h>
# define MAX 500 //表示两结点没有边
# define ModeNumber 100
void main()
{
void findpath( int i,int j,int p[][ModeNumber+1],int *mid);
int n,i,j,k;
cout<<"输入有向图的结点数:";
cin>>n;
int p[ModeNumber+1][ModeNumber+1];
//记录顶点i-->j中间经过的其他顶点
int *mid=new int[n+1]; //辅助寻找并记录顶点i到j的路径
int **D; //记录两顶点间的距离
D=new int *[n+1];
for(i=0;i<=n;i++)
D[i]=new int[n+1];
cout<<"将含有"<<n<<"个顶点的有向图边的信息录入到矩阵D["<<n<<"]"
<<"["<<n<<"]中:"<<endl;
cout<<"(注:若两个顶点没有路径,请输入"<<MAX<<")"<<endl;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
cin>>D[i][j];
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
if(D[i][j]!=MAX)
p[i][j]=0; //0代表顶点i与j间有直接路径;
else
p[i][j]=-1; //-1代表顶点i与j间没有直接路径;
}//当p[i][j]的值为1到n时,代表从顶点i到j经过该顶点;
}
cout<<endl;
cout<<"有向图的初始边矩阵D["<<n<<"]"<<"["<<n<<"]为:("<<MAX<<"代表没有直接路径)"<<endl;
cout<<endl;
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
cout<<setw(5)<<D[i][j]<<" ";
cout<<endl;
}
//当i-->j距离大于i-->k-->j距离时,令D[i][j]=D[i][k]+D[k][j],同时令p[i][j]=k
for(k=1;k<=n;k++)
{
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(D[i][j]>(D[i][k]+D[k][j]))
{
D[i][j]=D[i][k]+D[k][j];
p[i][j]=k;
}
}
cout<<endl;
cout<<"有向图的最终权值矩阵D["<<n<<"]"<<"["<<n<<"]为:"<<endl;
cout<<endl;
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
cout<<setw(5)<<D[i][j]<<" ";
cout<<endl;
}
cout<<endl;
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
if(i!=j)
{
if(p[i][j]==-1)
cout<<setw(3)<<i<<" -->"<<setw(3)<<j<<"没有路径"<<endl;
else
{
if(p[i][j]==0)
{
cout<<"顶点"<<setw(3)<<i<<"-->"<<j<<setw(10)<<"的距离为:"<<setw(3)<<D[i][j]<<" 路径为: ";
cout<<i<<"-->"<<j<<endl;
}
else
{
mid[0]=0;
findpath(i,j,p,mid);
cout<<"顶点"<<setw(3)<<i<<"-->"<<j<<setw(10)<<"的距离为:"<<setw(3)<<D[i][j]<<" 路径为: ";
for(k=1;k<=mid[0];k++)
cout<<mid[k]<<"-->";
cout<<j;
cout<<endl;
}
}
}
}
}
delete []D;
delete []mid;
}
void findpath(int i,int j,int p[][ModeNumber+1],int *mid)
{
if(p[i][j]!=0)//顶点i与j不是直接到达
{
findpath(i,p[i][j],p,mid);
findpath(p[i][j],j,p,mid);
}
else //顶点i与j直接到达,将顶点i放入mid[]中保存
{
mid[0]++;
mid[mid[0]]=i;
}
}
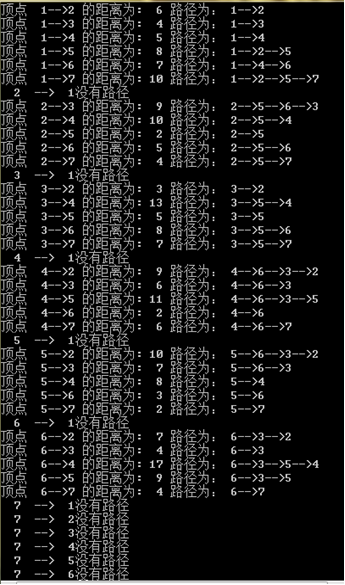
测试结果
输入下图数据:
运行结果
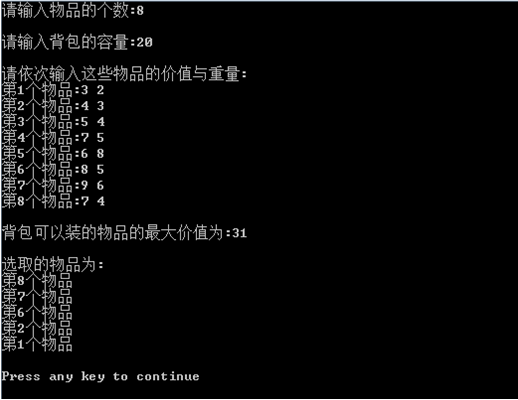
0-1背包问题
问题描述:
采用动态规划算法实现从n个物品中选择i(0≤i≤n)个物品装入容量为C的背包中,使得装入背包中的物品的总价值最大。
算法描述:为了装满背包,我们导出一个递归公式如下,设V[i][j]用来表示从前i项中取出来的装入容量为j的背包的物品的最大价值。这里i的范围是从0到n,j的范围是从0到C。这样,要求的是值V[n][C]。很清楚,V[0][j]对于所有j的值是0,这是由于背包中什么也没有。另一方面,V[i][0]对于所有i的值为0,因为没有东西可以放到容量为0的背包里。递推公式如下:
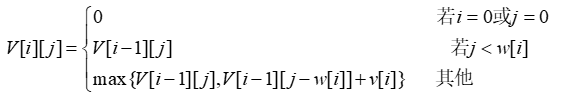
算法分析:时间复杂度是Θ(nC),其空间复杂度是Ω(nC)。
#include<stdio.h>
#include<stdlib.h>
#define N 100
void knapsack(int v[N],int w[N],int n,int C);
void main()
{
int i,n,C; /* n是物品的个数,C是背包的容量*/
int v[N],w[N]; /* v[i]存放第i个物品的价值,w[i]存放第i个物品的重量*/
printf("请输入物品的个数:");
scanf("%d",&n);
printf("\n请输入背包的容量:");
scanf("%d",&C);
printf("\n请依次输入这些物品的价值与重量:\n");
for(i=1;i<=n;i++)
{
printf("第%d个物品:",i);
scanf("%d%d",&v[i],&w[i]);
}
knapsack(&v,&w,n,C); /* 调用子函数knapsack*/
}
//子函数knapsack()具体实现使放入容量为C的背包中的物品的总价值最大
void knapsack(int v[N],int w[N],int n,int C)
{
int i,j,k;int keep[N][N];int V[N][N];
for(i=0;i<=C;i++)
V[0][i]=0;
for(i=0;i<=n;i++)
V[i][0]=0;
for(i=1;i<=n;i++)
for(j=1;j<=C;j++)
{
if((w[i]<=j)&&((v[i]+V[i-1][j-w[i]])>V[i-1][j]))
{
V[i][j]=v[i]+V[i-1][j-w[i]];
keep[i][j]=1; /*记录当背包容量为j时,可以放入第i个物品*/
}
else
{
V[i][j]=V[i-1][j];
keep[i][j]=0;
}
}
printf("\n背包可以装的物品的最大权值为:%d\n",V[n][C]);
printf("\n选取的物品为:\n");
k=C;
for(i=n;i>=1;i--)
{
if(keep[i][k]==1)
{
printf("第%d个物品\n",i);
k=k-w[i];
}
}
printf("\n");
}
测试结果
贪心算法
一、基本思想
贪心算法的基本思想是在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解,再将所有的这些局部最优解合起来形成整体上的一个最优解。
二、使用贪心算法的问题必须满足下面的两个性质:
1.整体的最优解可以通过局部的最优解来求出;
2.一个整体能够被分为多个局部,并且这些局部都能够求出最优解。
三、解决的问题:
最短路径问题、最小耗费生成树(Prim算法和kmskal算法)、文件压缩
四、贪心算法的基本步骤 :
1、从问题的某个初始解出发。
2、采用循环语句,当可以向求解目标前进一步时,就根据局部最优策略,得到一个部分解,缩小问题的范围或规模。
3、将所有部分解综合起来,得到问题的最终解。
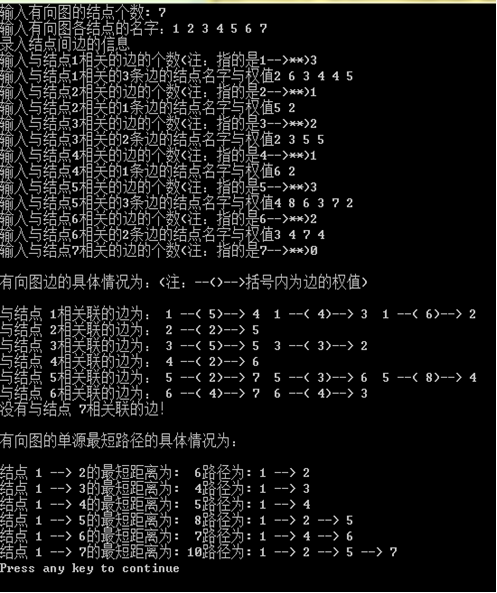
单源点最短路径问题
问题描述:
设G=(V,E)是一个有向图,其中的每条边(i,j)有一个非负的长度权值w[i,j],其中有一个源点d(图中选定1节点为源点),要确定从d到V中每个其他顶点的距离,min[n]是一个存放从源点d到任意顶点i的最短路径长度的数组。
实验数据:
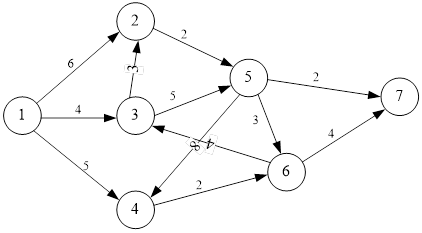
设V={1,2,…,n},s=1。X存放这些从源点到该结点的距离已经确定的结点,Y存放距离还未确定的结点,prenode[]存放该结点的直接前驱,dis[]存放源点到其他结点的距离。初始时,先将顶点分为两部分,X={1}和Y={2,3,…,n}。先将源点的所有后继结点的权值赋值给相应的dis[],同时这些结点的先驱结点在prenode []的相应位置赋值为1。接下来,每次从dis[]里选出权值最小的结点y,将其从Y中移到X中,检查y的后继结点yi,若存在dis[yi]>dis[y]+length(y->yi)则修改dis[yi]的值为dis[y]+length(y->yi)同时修改prenode[yi]的值为y。重复上述操作直到Y变为空集。此时,dis[]里存放了源点到所有其他结点的最短距离,prenode[]存放了源点到其他所有结点的最短距离路径的直接前驱。
# include <iostream.h>
# include <stdio.h>
# include <stdlib.h>
# include <iomanip.h>
# define MAX 500 //此值比该有向图的所有边的权值都大
typedef struct node //定义边结点类型
{
int number; //顶点名
int power; //该边权值
struct node *next;
}node,*Point;
void main()
{
int n,i,j,p,q,r;
cout<<"输入有向图的结点个数: ";
cin>>n;
int *name=new int[n+1]; //存放各个结点的名字
int *prenode=new int[n+1]; //存放结点name[i]的先驱结点
int *dis=new int[n+1]; //存放结点name[1]到其他结点的最短距离
cout<<"输入有向图各结点的名字:";
for(i=1;i<=n;i++)
cin>>name[i];
Point mid;
node *edge=new node[n+1]; //存放有向图的边的信息
for(i=1;i<=n;i++)
{
edge[i].number=name[i];
edge[i].power=0;
edge[i].next=NULL;
}
cout<<"录入结点间边的信息"<<endl;
for(i=1;i<=n;i++)
{
cout<<"输入与结点"<<name[i]<<"相关的边的个数(注:指的是"<<i<<"-->**)";
cin>>j;
edge[i].power=j;
if(j>0)
{
cout<<"输入与结点"<<name[i]<<"相关的"<<j<<"条边的结点名字
与权值";
while(j>0)
{
mid=(Point)malloc(sizeof(node));
cin>>(*mid).number>>(*mid).power;
(*mid).next=edge[i].next;
edge[i].next=mid;
j--;
}
}
}
cout<<endl;
cout<<"有向图边的具体情况为:(注:--()-->括号内为边的权值)"<<endl;
cout<<endl;
for(i=1;i<=n;i++)
{
mid=edge[i].next;
if(mid!=NULL)
{
cout<<"与结点"<<setw(2)<<edge[i].number<<"相关联的边为:";
while(mid!=NULL)
{
cout<<setw(2)<<edge[i].number<<setw(4)<<"--("<<setw(2)
<<(*mid).power<<")-->"<<setw(2)<<(*mid).number<<" ";
mid=(*mid).next;
}
}
else cout<<"没有与结点"<<setw(2)<<edge[i].number<<"相关联的边!";
cout<<endl;
}
dis[1]=0;
for(i=2;i<=n;i++)
dis[i]=MAX;
prenode[1]=0;
mid=edge[1].next;
//先将源点的所有后继结点的权值赋值给相应的dis[],这些结点的先驱结点赋值为name[1]
while(mid!=NULL)
{
dis[(*mid).number]=(*mid).power;
prenode[(*mid).number]=1;
mid=(*mid).next;
}
p=2; //name
for(i=1;i<n;i++) //其他n-1个结点
{
q=MAX;//distance
for(j=p;j<=n;j++)
if(dis[name[j]]<q) //选出dis[]里的最小权值
{
q=dis[name[j]];
r=j; //记录最小权值结点在name[]中的位置
}
j=name[p];//将最小权值所对应的在name[]的位置与p所代表的位置互换,
name[p]=name[r];
name[r]=j; //p位置前部分为找到最短路径的结点,后部分为未找到的结点
mid=edge[name[p]].next;
//检查刚找到最短路径f结点的后继结点fi,若(1-->f)+(f-->fi)的距离小于
//1-->fi的直接距离,修改fi在dis[]中的相应值为该较小值,并修改fi的
//直接前驱为f
while(mid!=NULL)
{
if((dis[name[p]]+(*mid).power)<dis[(*mid).number])
{
dis[(*mid).number]=dis[name[p]]+(*mid).power;
prenode[(*mid).number]=name[p];
}
mid=(*mid).next;
}
p++;
}
cout<<endl; cout<<"有向图的单源最短路径的具体情况为:"<<endl;
cout<<endl;
for(i=2;i<=n;i++)
{
p=n; name[p]=i; //此处name[]用来存放路径
r=prenode[i];
while(r!=0) //prenode[1]=0
{ p--; name[p]=r; r=prenode[r]; }
cout<<"结点"<<setw(2)<<edge[1].number<<setw(4)<<"-->"<<setw(2)<<i
<<"的最短距离为:"<<setw(3)<<dis[i]<<"路径为:";
for(j=p;j<=n;j++)
{
if(j!=n)
cout<<setw(2)<<name[j]<<setw(4)<<"-->";
else
cout<<setw(2)<<name[j];
}
cout<<endl;
}
delete []name;
delete []prenode;
delete []dis;
delete []edge;
}
测试结果
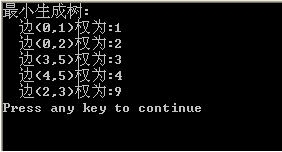
最小耗费生成树(Kruskal)
问题描述:
用Kruskal算法求最小生成树。设G=(V,E)是一个有n个顶点的无向带权连通图,如果i,j之间有边相连w[i][j]为i与j相连接的边的权值,否则w[i][j]=0,将图中边按其权值由小到大的次序顺序选取,若选边后不形成回路,则保留作为一条边,若形成回路则除去.依次选够(n-1)条边,即得最小生成树.
#include <stdio.h>
#define MAXVEX 100
typedef struct
{
int u; /*边的起始顶点*/
int v; /*边的终止顶点*/
int w; /*边的权值*/
} Edge;
void Kruskal(Edge E[],int n,int e)
{
int i,j,m1,m2,sn1,sn2,k;
int vset[MAXVEX];
for (i=0;i<n;i++) vset[i]=i; /*初始化辅助数组*/
k=1; /*k表示构造最小生成树的第几条边,初值为1*/
j=0; /*E中边的下标,初值为0*/
while (k<n) /*生成的边数小于n时循环*/
{
m1=E[j].u;m2=E[j].v; /*取一条边的头尾顶点*/
sn1=vset[m1];sn2=vset[m2]; /*分别得到两个顶点所属的集合编号*/
if (sn1!=sn2) /*两顶点属不同的集合,该边是最小生成树的边*/
{
printf(" 边(%d,%d)权为:%d\n",m1,m2,E[j].w);
k++; /*生成边数增1*/
for (i=0;i<n;i++) /*两个集合统一编号*/
if (vset[i]==sn2) /*集合编号为sn2的改为sn1*/
vset[i]=sn1;
}
j++; /*扫描下一条边*/
}
}
void main()
{
int n=6,e=9;
Edge E[]={
{0,1,1},{0,2,2},{3,5,3},
{4,5,4},{1,2,6},{3,4,7},
{2,3,9},{1,3,11},{2,4,13}
};
printf("最小生成树:\n");Kruskal(E,n,e);
}

测试结果
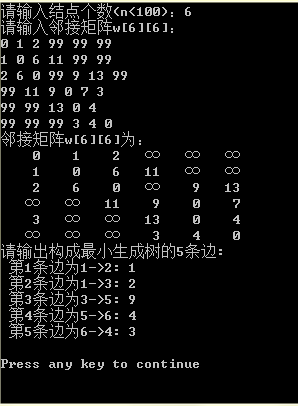
最小耗费生成树(Prim)
问题描述:
用Prim算法求最小生成树。设G=(V,E)是一个有n个顶点的无向带权连通图,如果i,j之间有边相连w[i][j]为i与j相连接的边的权值,否则w[i][j]=0,找出该图中的一个含有n-1条边的子图,使得这n-1条边的权值和最小。
实验数据:

设所给定无向加权连通图具有n个结点,m条边。算法从建立两个顶点集合开始:X={1}和Y{2,3,…,n}。接着每次取一条边,生成一棵生成树。每次,它找出一条权重最小的边,分别在X[n],Y[n]中做标记,直至Y[n]为空,此时生成树有n-1条边,我们所得到的就是一棵最小生成树。
#include<stdio.h>
#define N 100
void main()
{
int i,j,n,
int min,k,p=0,q=0; //n是结点个数
int w[N][N]; //记录边的权值
bool X[N],Y[N]; //X[N]和Y[N]是两个顶点集
int tree[N][3]; //存放最短路径的边及其权值
printf("请输入结点个数(n<100):");
scanf("%d",&n);
//X[i]=1:元素i在集合X[n]中,X[i]=0:元素i不在集合X[n]中。初始时刻,只有结点1在集合X[n]中,即X[1]=1。
X[1]=1;
//Y[j]=1:元素j在集合Y[n]中,Y[j]=0:元素j不在集合Y[n]中。Y[j]由1变为0,这时X[j]由0变为1,说明元素j从集合Y[n]移动到X[n]中;初始时刻,只有结点0不在集合Y[n]中,即Y[1]=1
Y[1]=0;
for(i=2;i<=n;i++) //初始时刻,不在集合X[n]中的元素:X[i]=0
X[i]=0;
for(i=2;i<=n;i++) //初始时刻,在集合Y[n]中的元素:Y[i]=1
Y[i]=1;
/*输入邻接矩阵w[n][n] */
w[0][0]=0;
for(i=1;i<=n;i++)
{
w[0][i]=i;
w[i][0]=i;
}
printf("请输入邻接矩阵w[%d][%d]:\n",n,n);
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
scanf("%d",&w[i][j]);
/*计算最小生成树的边*/
for(k=0;k<n-1;k++)
{
for(i=1;i<=n;i++) //找出集合X[n]中的某个顶点i
if(X[i]!=0) break;
for(j=2;j<=n;j++) //找出集合Y[n]中的某个顶点j
if(Y[j]!=0) break;
min=w[i][j]; //将集合X[n]中结点i到集合Y[n]中结点j的权值w[i][j]设置为最小值
p=i; //p代表集合X[n]中的结点
q=j; //q代表集合Y[n]中的结点
for(i=1;i<=n;i++)
{
if(X[i]!=0) //找出集合X[n]中的一个结点
{
for(j=2;j<=n;j++) //找出集合X[n]中的一个结点i到集合Y[n]中的任意一个结点j的权值w[i][j]的最小值,记录在min中,并用p、q记录下他们的坐标
{
if(Y[j]!=0) //找出集合Y[n]中的一个结点
{
if(min>w[i][j])
{
min=w[i][j];
p=i;
q=j; //q记录权值最小边中,在集合Y中的结点
}
}
}
}
}
X[q]=1; //将权值最小边中结点在集合Y[n]中的结点移动到集合X[n]中
Y[q]=0;
tree[k][0]=p; //记录下最小边初始顶点的坐标
tree[k][1]=q; //记录下最小边终止顶点的坐标
tree[k][2]=w[p][q]; //记录下最小边的权值
}
printf("邻接矩阵w[%d][%d]为:\n",n,n);
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
if(w[i][j]!=99)
printf("%5d",w[i][j]);
else
printf(" ∞");
printf("\n");
}
//输出构成最小生成树的边
printf("请输出构成最小生成树的%d条边:",n-1);
for(i=0;i<n-1;i++)
printf("\n 第%d条边为%d->%d: %d",i+1,tree[i][0],tree[i][1],tree[i][2]);
printf("\n\n");
}
测试结果
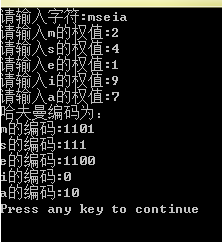
Huffman编码
问题描述:
Huffman采取变长编码的策略压缩存放一n个字符的字符串文件,每个字符有一个权值wi, 试构造一颗有n个叶子节点的二叉树,其中树带权路径最小的二叉树成为哈夫曼树或者最优二叉树。
weight为输入的频率数组,把其中的值赋给依次建立的HT Node对象中的data属性,即每一个HT Node对应一个输入的频率。然后根据data属性按从小到大顺序排序,每次从data取出两个最小和此次小的HT Node,将他们的data相加,构造出新的HTNode作为他们的父节点,指针parent,leftchild,rightchild赋相应值。在把这个新的节点插入最小堆。按此步骤可以构造构造出一棵哈夫曼树。
通过已经构造出的哈夫曼树,自底向上,由频率节点开始向上寻找parent,直到parent为树的顶点为止。这样,根据每次向上搜索后,原节点为父节点的左孩子还是右孩子,来记录1或0,这样,每个频率都会有一个01编码与之唯一对应,并且任何编码没有前部分是同其他完整编码一样的。
#include<stdio.h>
#include<string.h>
#include<malloc.h>
#define M 50
#define MAX 1000;
typedef struct
{
int weight; //结点权值
int parent,lchild,rchild;
}HTNODE,*HUFFMANTREE;
typedef char** HUFFMANCODE; //动态分配数组存储哈夫曼编码表
HUFFMANTREE huffmantree(int n,int weight[]) //构建哈夫曼树
{
int m1,m2,k;
int i,j,x1,x2;
HUFFMANTREE ht;
ht=(HUFFMANTREE)malloc((2*n)*sizeof(HTNODE));
for(i=1;i<(2*n);i++)
//初始化哈夫曼树中各结点的数据,没初始值的赋值为0
{
ht[i].parent=ht[i].lchild=ht[i].rchild=0;
if(i<=n)
ht[i].weight=weight[i];
else
ht[i].weight=0;
}
for(i=1;i<n;i++)
//每一重循环从森林中选择最小的两棵树组建成一颗新树
{
m1=m2=MAX;
x1=x2=0;
for(j=1;j<(n+i);j++)
{
if((ht[j].weight<m1)&&(ht[j].parent==0))
{
m2=m1;
x2=x1;
m1=ht[j].weight;
x1=j;
}
else
if((ht[j].weight<m2)&&(ht[j].parent==0))
{
m2=ht[j].weight;
x2=j;
}
}
k=n+i;
ht[x1].parent=ht[x2].parent=k;
ht[k].weight=m1+m2;
ht[k].lchild=x1;
ht[k].rchild=x2;
}
return ht;
}
void huffmancoding(const int n,HUFFMANCODE hc,HUFFMANTREE ht,char str[])
{
int i,start,child,father;
char *cd;
hc=(HUFFMANCODE)malloc((n+1)*sizeof(char*)); //分配n个字符编码的头指针
cd=(char*)malloc(n*sizeof(char)); //分配求编码的工作空间
cd[n-1]='\0'; //编码结束符
for(i=1;i<=n;++i) //逐个字符求哈夫曼编码
{
start=n-1;
for(child=i,father=ht[i].parent;father!=0;child=father,father=ht[father].parent)
/*从叶子结点到根结点求逆向编码*/
if(ht[father].lchild==child)
cd[--start]='0';
else
cd[--start]='1';
hc[i]=(char*)malloc((n-start)*sizeof(char)); //为i个字符编码分配空间
strcpy(hc[i],&cd[start]); //从cd复制哈夫曼编码串到hc
}
free(cd); //释放工作空间
printf("哈夫曼编码为:\n");
for(i=1;i<=n;++i)
{
printf("%c的编码:",str[i]);
printf("%s\n",hc[i]);
}
}
void main()
{
int j,k;
char str[50];
int weight[50];
printf("请输入字符:");
gets(str);
for(j=0;j<50;j++)
{
if(str[j]=='\0')
break;
}
const int n=j;
for(j=n;j>0;j--)
str[j]=str[j-1];
str[n+1]='\0';
for(k=0;k<n;k++)
{
printf("请输入%c的权值:",str[k+1]);
scanf("%d",&weight[k]);
}
for(k=n;k>0;k--)
weight[k]=weight[k-1];
weight[0]=0;
HUFFMANCODE hc=NULL;
HUFFMANTREE ht;
ht=huffmantree(n,weight);
huffmancoding(n,hc,ht,str);
}
测试结果
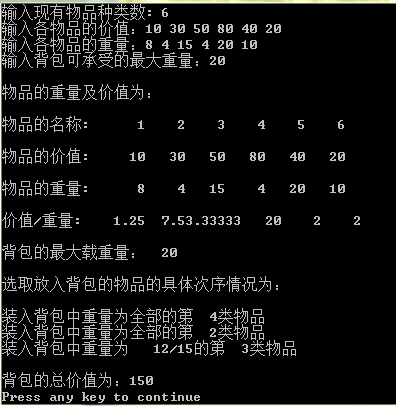
分数背包
问题描述:
给定n种物品以及一个最大承重量为Z的背包,其中任意物品i的重量是W[i],价值是V[i]。分数背包问题是解决将任意数量的物品装满背包,在不超过背包最大载重量Z的前提下,使背包内物品的总价值最大的问题。
此问题用贪心算法策略求解。首先,计算出每个物品的价值与重量之比,再将比值由大到小排序。接下来重复下面的操作:每次从未选择的物品集合中选择性价比最大的物品,如果将其放入背包后,背包的重量仍小于等于背包的容量,说明该物品可以完全装入;如果背包里物品的重量小于背包的容量,并且不能放入一个性价比高的整个物品,则将这个物品的一部分装入背包,使背包里物品的重量达到背包的容量;直到背包达到最大容量结束。最后输出背包里面的物品
# include<stdio.h>
# include <iostream.h>
# include <stdio.h>
# include <iomanip.h>
#define N 100
void main()
{
int i,j,m;
int n,Weight;//物品的种类数、背包可承受的最大重量
double WholeValue,mid;//背包价值
cout<<"输入现有物品种类数: ";
cin>>n;
double *Value=new double(n+1);//存放各物品的价值
double *V=new double(n+1);//存放各物品的价值/重量
int *W=new int(n+1);//存放各物品的重量
int *P=new int(n+1);//存放各物品的名称
cout<<"输入各物品的价值:";
for(i=1;i<=n;i++)
{ cin>>Value[i];
}
cout<<"输入各物品的重量:";
for(i=1;i<=n;i++)
cin>>W[i];
cout<<"输入背包可承受的最大重量:";
cin>>Weight;
cout<<endl;
for(i=1;i<=n;i++)
{
V[i]=Value[i]/W[i];
P[i]=i;
}
cout<<"物品的重量及价值为:"<<endl;
cout<<endl;
cout<<"物品的名称:"<<" ";
for(i=1;i<=n;i++)
cout<<setw(5)<<i;
cout<<endl;
cout<<endl;
cout<<"物品的价值:"<<" ";
for(i=1;i<=n;i++)
cout<<setw(5)<<Value[i];
cout<<endl;
cout<<endl;
cout<<"物品的重量:"<<" ";
for(i=1;i<=n;i++)
cout<<setw(5)<<W[i];
cout<<endl;
cout<<endl;
cout<<"价值/重量: "<<" ";
for(i=1;i<=n;i++)
cout<<setw(5)<<V[i];
cout<<endl;
cout<<endl;
cout<<"背包的最大载重量: "<<Weight<<endl;
cout<<endl;
for(i=n;i>1;i--) //重新将矩阵V[]按物品的(价值/重量)由高到低排列
for(j=2;j<=i;j++)
if(V[j-1]<V[j])
{
mid=V[j]; V[j]=V[j-1]; V[j-1]=mid;
mid=Value[j]; Value[j]=Value[j-1]; Value[j-1]=mid;
m=P[j]; P[j]=P[j-1]; P[j-1]=m;
m=W[j]; W[j]=W[j-1]; W[j-1]=m;
}
m=Weight;
i=1;
WholeValue=0.0;
cout<<"选取放入背包的物品的具体次序情况为:"<<endl;
cout<<endl;
while(m>0) //按物品(价值/重量)由高到低进行选择
{
if(m>=W[i]) //当背包还可放入第i类物品的总重量,将其全部放入
{
WholeValue=Value[i]+WholeValue;
cout<<"装入背包中重量为"<<setw(5)<<"全部的第"<<setw(3)
<<P[i]<<"类物品"<<endl;
m=m-W[i];
i++;
}
else//背包不可放入全部的第i类物品,将背包剩余容量全部放入i物品
{
WholeValue=WholeValue+m*Value[i]/W[i];
cout<<"装入背包中重量为"<<setw(5)<<m<<"/"<<W[i]<<"的第"<<setw(3)
<<P[i]<<"类物品"<<endl;
m=0;
break; //可供选择的物品已被选取完
}
}
cout<<endl;
cout<<"背包的总价值为:"<<WholeValue<<endl;
}
测试结果
图算法
深度优先搜索
将邻接矩阵转换成邻接表void MatToList(AdjMatix g,AdjList *&G)
输出图的邻接表表示void DispAdjList(AdjList *G)
递归方法进行深度优先遍历void DFS(AdjList *g,int vi)
非递归方法进行深度优先遍历void DFS1(AdjList *G,int vi)
#include <stdio.h>
#include <malloc.h>
#include <string.h>
#define MAXVEX 100
typedef char VertexType[3]; /*定义VertexType为char数组类型*/
typedef struct vertex
{
int adjvex; /*顶点编号*/
VertexType data; /*顶点的信息*/
} VType; /*顶点类型*/
typedef struct graph
{
int n,e; /*n为实际顶点数,e为实际边数*/
VType vexs[MAXVEX]; /*顶点集合*/
int edges[MAXVEX][MAXVEX]; /*边的集合*/
} AdjMatix; /*图的邻接矩阵类型*/
typedef struct edgenode
{
int adjvex; /*邻接点序号*/
int value; /*边的权值*/
struct edgenode *next; /*下一条边的顶点*/
} ArcNode; /*每个顶点建立的单链表中结点的类型*/
typedef struct vexnode
{
VertexType data; /*结点信息*/
ArcNode *firstarc; /*指向第一条边结点*/
} VHeadNode; /*单链表的头结点类型*/
typedef struct
{
int n,e; /*n为实际顶点数,e为实际边数*/
VHeadNode adjlist[MAXVEX]; /*单链表头结点数组*/
} AdjList; /*图的邻接表类型*/
void DispAdjList(AdjList *G)
{
int i;
ArcNode *p;
printf("图的邻接表表示如下:\n");
for (i=0;i<G->n;i++)
{
printf(" [%d,%3s]=>",i,G->adjlist[i].data);
p=G->adjlist[i].firstarc;
while (p!=NULL)
{
printf("(%d,%d)->",p->adjvex,p->value);
p=p->next;
}
printf("∧\n");
}
}
void MatToList(AdjMatix g,AdjList *&G) /*将邻接矩阵g转换成邻接表G*/
{
int i,j;
ArcNode *p;
G=(AdjList *)malloc(sizeof(AdjList));
for (i=0;i<g.n;i++) /*给邻接表中所有头结点的指针域置初值*/
{
G->adjlist[i].firstarc=NULL;
strcpy(G->adjlist[i].data,g.vexs[i].data);
}
for (i=0;i<g.n;i++) /*检查邻接矩阵中每个元素*/
for (j=g.n-1;j>=0;j--)
if (g.edges[i][j]!=0) /*邻接矩阵的当前元素不为0*/
{
p=(ArcNode *)malloc(sizeof(ArcNode));/*创建一个结点*p*/
p->value=g.edges[i][j];p->adjvex=j;
p->next=G->adjlist[i].firstarc; /*将*p链到链表后*/
G->adjlist[i].firstarc=p;
}
G->n=g.n;G->e=g.e;
}
int visited[MAXVEX];
void DFS(AdjList *g,int vi) /*对邻接表G从顶点vi开始进行深度优先遍历*/
{
ArcNode *p;
printf("%d ",vi); /*访问vi顶点*/
visited[vi]=1; /*置已访问标识*/
p=g->adjlist[vi].firstarc; /*找vi的第一个邻接点*/
while (p!=NULL) /*找vi的所有邻接点*/
{
if (visited[p->adjvex]==0)
DFS(g,p->adjvex); /*从vi未访问过的邻接点出发深度优先搜索*/
p=p->next; /*找vi的下一个邻接点*/
}
}
void DFS1(AdjList *G,int vi) /*非递归深度优先遍历算法*/
{
ArcNode *p;
ArcNode *St[MAXVEX];
int top=-1,v;
printf("%d ",vi); /*访问vi顶点*/
visited[vi]=1; /*置已访问标识*/
top++; /*将初始顶点vi的firstarc指针进栈*/
St[top]=G->adjlist[vi].firstarc;
while (top>-1) /*栈不空循环*/
{
p=St[top];top--; /*出栈一个顶点为当前顶点*/
while (p!=NULL) /*循环搜索其相邻顶点*/
{
v=p->adjvex; /*取相邻顶点的编号*/
if (visited[v]==0) /*若该顶点未访问过*/
{
printf("%d ",v); /*访问v顶点*/
visited[v]=1; /*置访问标识*/
top++; /*将该顶点的第1个相邻顶点进栈*/
St[top]=G->adjlist[v].firstarc;
break; /*退出当前顶点的搜索*/
}
p=p->next; /*找下一个相邻顶点*/
}
}
}
void main()
{
int i,j;
AdjMatix g;
AdjList *G;
int a[5][5]={{0,1,0,1,0},{1,0,1,0,0},{0,1,0,1,1},{1,0,1,0,1},{0,0,1,1,0}};
char *vname[MAXVEX]={"a","b","c","d","e"};
g.n=5;g.e=12; /*建立无向图,每1条无向边算为2条有向边*/
for (i=0;i<g.n;i++)
strcpy(g.vexs[i].data,vname[i]);
for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
g.edges[i][j]=a[i][j];
MatToList(g,G); /*生成邻接表*/
DispAdjList(G); /*输出邻接表*/
for (i=0;i<g.n;i++) visited[i]=0; /*顶点标识置初值*/
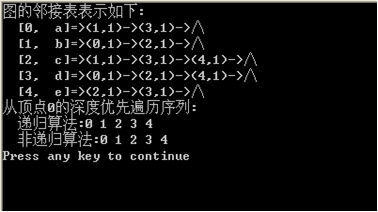
printf("从顶点0的深度优先遍历序列:\n");
printf(" 递归算法:");DFS(G,0);printf("\n");
for (i=0;i<g.n;i++) visited[i]=0; /*顶点标识置初值*/
printf(" 非递归算法:");DFS1(G,0);printf("\n");
}
测试结果
广度优先搜索
将邻接矩阵转换成邻接表void MatToList(AdjMatix g,AdjList *&G)
输出图的邻接表表示void DispAdjList(AdjList *G)
非递归方法进行广度优先搜索void BFS(AdjList *G,int vi)
#include <stdio.h>
#include <malloc.h>
#include <string.h>
#define MAXVEX 100
typedef char VertexType[3]; /*定义VertexType为char数组类型*/
typedef struct vertex
{
int adjvex; /*顶点编号*/
VertexType data; /*顶点的信息*/
} VType; /*顶点类型*/
typedef struct graph
{
int n,e; /*n为实际顶点数,e为实际边数*/
VType vexs[MAXVEX]; /*顶点集合*/
int edges[MAXVEX][MAXVEX]; /*边的集合*/
} AdjMatix; /*图的邻接矩阵类型*/
typedef struct edgenode
{
int adjvex; /*邻接点序号*/
int value; /*边的权值*/
struct edgenode *next; /*下一条边的顶点*/
} ArcNode; /*每个顶点建立的单链表中结点的类型*/
typedef struct vexnode
{
VertexType data; /*结点信息*/
ArcNode *firstarc; /*指向第一条边结点*/
} VHeadNode; /*单链表的头结点类型*/
typedef struct
{
int n,e; /*n为实际顶点数,e为实际边数*/
VHeadNode adjlist[MAXVEX]; /*单链表头结点数组*/
} AdjList; /*图的邻接表类型*/
void DispAdjList(AdjList *G)
{
int i;
ArcNode *p;
printf("图的邻接表表示如下:\n");
for (i=0;i<G->n;i++)
{
printf(" [%d,%3s]=>",i,G->adjlist[i].data);
p=G->adjlist[i].firstarc;
while (p!=NULL)
{
printf("(%d,%d)->",p->adjvex,p->value);
p=p->next;
}
printf("∧\n");
}
}
void MatToList(AdjMatix g,AdjList *&G) /*将邻接矩阵g转换成邻接表G*/
{
int i,j;
ArcNode *p;
G=(AdjList *)malloc(sizeof(AdjList));
for (i=0;i<g.n;i++) /*给邻接表中所有头结点的指针域置初值*/
{
G->adjlist[i].firstarc=NULL;
strcpy(G->adjlist[i].data,g.vexs[i].data);
}
for (i=0;i<g.n;i++) /*检查邻接矩阵中每个元素*/
for (j=g.n-1;j>=0;j--)
if (g.edges[i][j]!=0) /*邻接矩阵的当前元素不为0*/
{
p=(ArcNode *)malloc(sizeof(ArcNode));/*创建一个结点*p*/
p->value=g.edges[i][j];p->adjvex=j;
p->next=G->adjlist[i].firstarc; /*将*p链到链表后*/
G->adjlist[i].firstarc=p;
}
G->n=g.n;G->e=g.e;
}
void BFS(AdjList *G,int vi) /*对邻接表g从顶点vi开始进行广度优先遍历*/
{
int i,v,visited[MAXVEX];
int Qu[MAXVEX],front=0,rear=0; /*循环队列*/
ArcNode *p;
for (i=0;i<G->n;i++) /*给visited数组置初值0*/
visited[i]=0;
printf("%d ",vi); /*访问初始顶点*/
visited[vi]=1; /*置已访问标识*/
rear=(rear=1)%MAXVEX; /*循环移动队尾指针*/
Qu[rear]=vi; /*初始顶点进队*/
while (front!=rear) /*队列不为空时循环*/
{
front=(front+1) % MAXVEX;
v=Qu[front]; /*顶点v出队*/
p=G->adjlist[v].firstarc; /*找v的第一个邻接点*/
while (p!=NULL) /*找v的所有邻接点*/
{
if (visited[p->adjvex]==0) /*未访问过则访问之*/
{
visited[p->adjvex]=1; /*置已访问标识*/
printf("%d ",p->adjvex);/*访问该点并使之入队列*/
rear=(rear+1) % MAXVEX; /*循环移动队尾指针*/
Qu[rear]=p->adjvex; /*顶点p->adjvex进队*/
}
p=p->next; /*找v的下一个邻接点*/
}
}
}
void main()
{
int i,j;
AdjMatix g;
AdjList *G;
int a[5][5]={{0,1,0,1,0},{1,0,1,0,0},{0,1,0,1,1},{1,0,1,0,1},{0,0,1,1,0}};
char *vname[MAXVEX]={"a","b","c","d","e"};
g.n=5;g.e=12; /*建立无向图,每1条无向边算为2条有向边*/
for (i=0;i<g.n;i++)
strcpy(g.vexs[i].data,vname[i]);
for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
g.edges[i][j]=a[i][j];
MatToList(g,G); /*生成邻接表*/
DispAdjList(G); /*输出邻接表*/
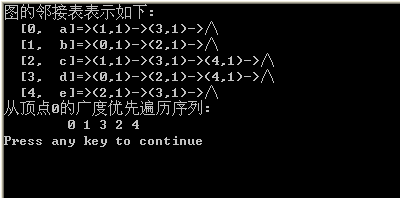
printf("从顶点0的广度优先遍历序列:\n");
printf("\t");BFS(G,0);printf("\n");
}
测试结果























 2633
2633











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








