Lumerical官方案例、FDTD时域有限差分法仿真学习（五）——液晶（liquid crystal）

本文链接：https://blog.csdn.net/weixin_45719141/article/details/123466632

一、单轴液晶的偏振特性
Polarization properties of a uniaxial liquid crystal

在这里插入图片描述

在这个例子中，我们将模拟一个简单的单轴 LCD 层。有关更复杂的 LC 方向，请参阅扭曲向列 LCD。

1.1 模拟设置

由液晶取向引起的各向异性导致沿液晶指向矢偏振的光以与沿垂直方向偏振的光不同的速度传播。这种双折射导致入射光和透过 LC 层的光之间的偏振发生变化。

为了在 FDTD 中模拟这种效果，我们将使用各向异性材料和 LC 网格属性对象，它允许我们为 LC 层指定任意方向。在这种情况下，我们所要做的就是在 LC 属性对象中设置与所需 LC 方向相对应的角度“theta”和“phi”。在 LCD.fsp 中，我们从在 x-y 平面上以 45 度偏振的平面波开始，并使用偏振椭圆分析组（polarization ellipse analysis group）来研究透射光的偏振变化。偏振椭圆分析对象可以在对象库（ object library）中找到，在远场投影（far field projections）部分。

1.1.1 各向异性材料

在这里插入图片描述

1.1.2 LC 网格属性对象

位置在Attributes
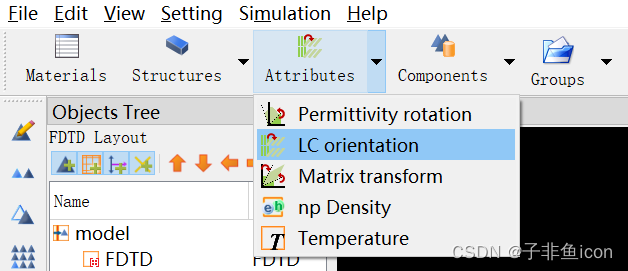
在这里插入图片描述
参数编辑

液晶指向为y轴

1.1.3 平面波光源

45度偏振
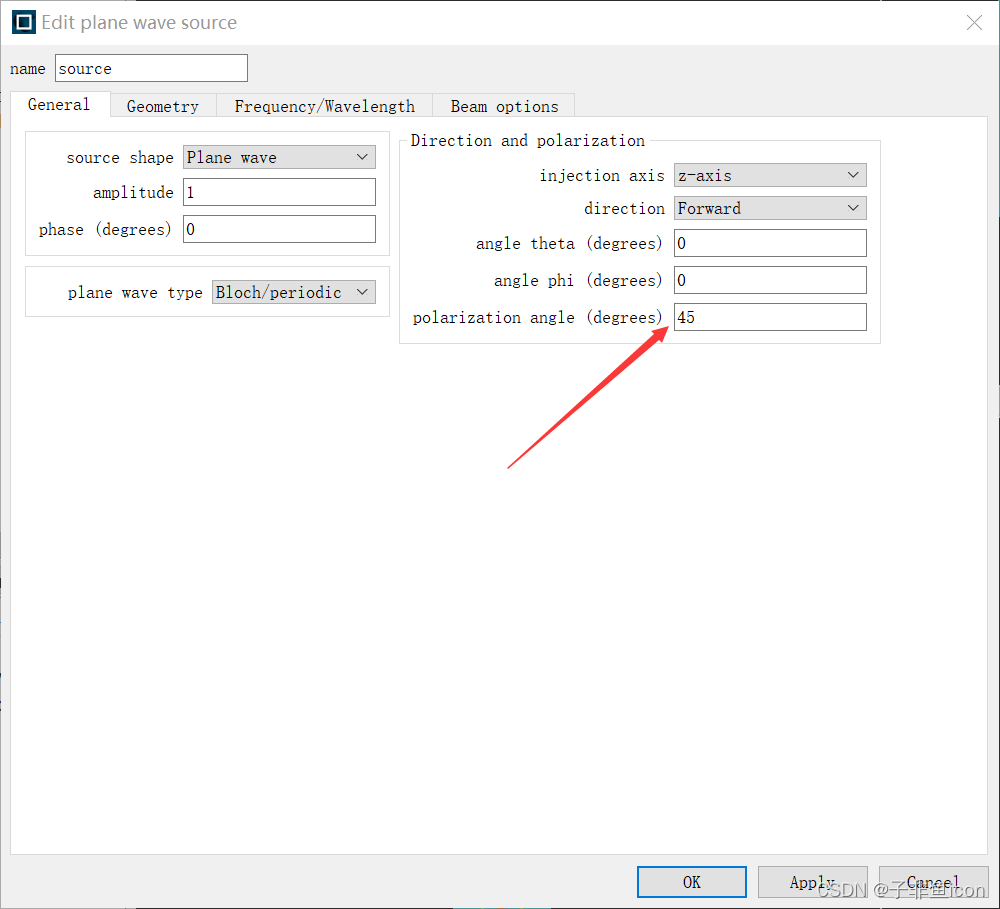
在这里插入图片描述
1.1.4 仿真区域

大小是个大长条，mesh accuracy设置为6，很高的精度

在这里插入图片描述
边界条件：x,y方向上周期边界条件，z上完全吸收、无反射。

除此之外，还设置了两个mesh，上下各一个。

1.1.5 偏振椭圆分析组

1.1.5.1 位置
在这里插入图片描述

在这里插入图片描述
1.1.5.2 Setup

varibables:

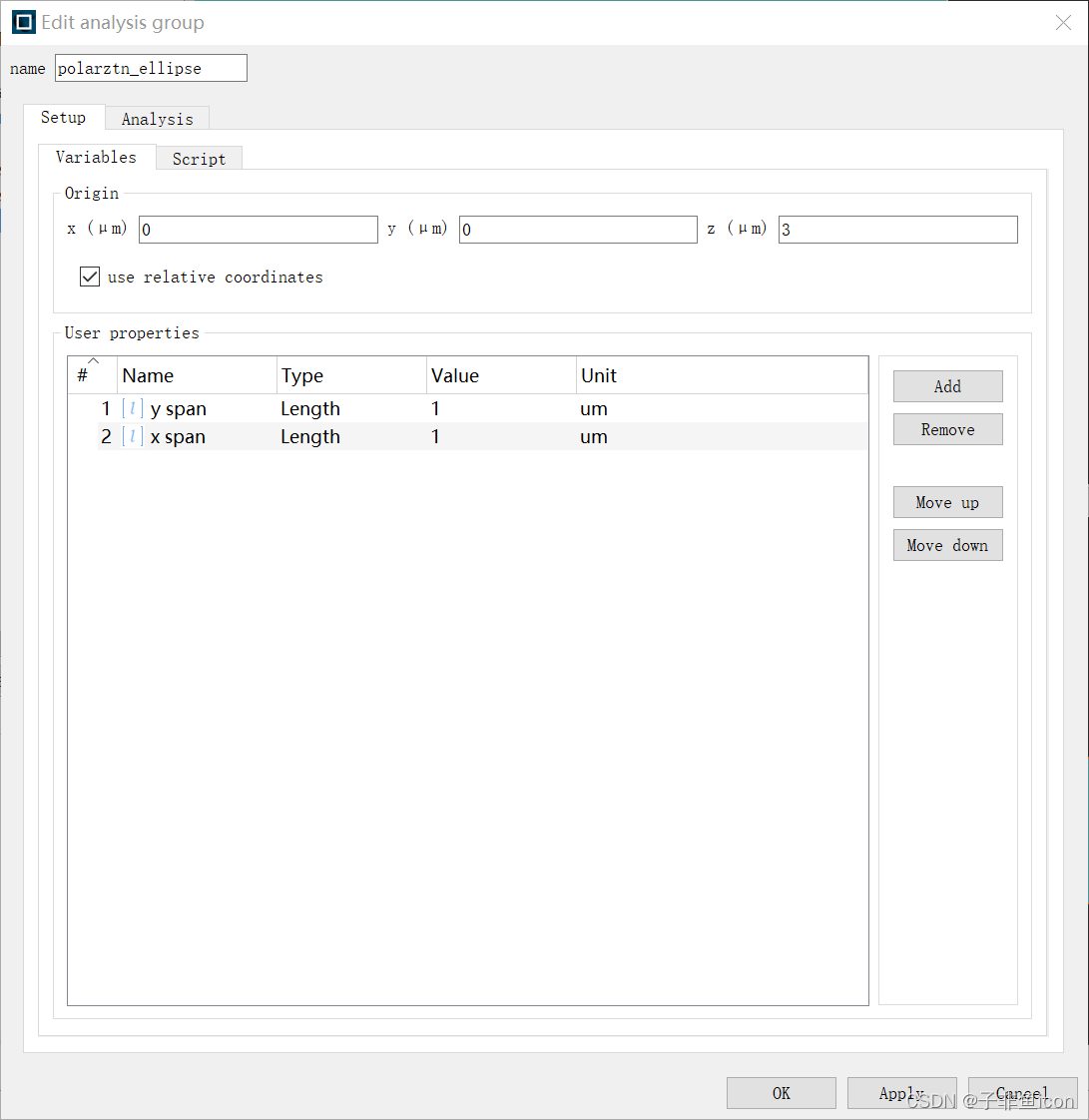
在这里插入图片描述
Script：

##############################################
# Polarization ellipse
# This script sets up the monitor size 该脚本设置监视器大小
#
# Input properties
# x,y span: span of the monitor
#
# Tags: far field polarization ellipse grating
#  远场偏振椭圆光栅
# Copyright 2012 Lumerical Solutions Inc
##############################################

# simplify variable names by removing spaces
x_span = %x span%;
y_span = %y span%;

select("field");
set("x",0);
set("y",0);
set("z",0);
set("x span",x_span);
set("y span",y_span);

1.1.5.3 Analysis

Variables:

4个参数：

f：感兴趣的频率
Gn、Gm：感兴趣的光栅阶次 (Gn,Gm)
make plots: 1 表示绘图，0 不绘制

2个输出属性：
major_angle：偏振椭圆长轴的角度
比率：长轴长度除以椭圆短轴长度
在这里插入图片描述
Script：

##############################################
# Polarization ellipse
# This script calculates the polarization of a grating order. 此脚本计算光栅阶的极化。
# The result is plotted in terms of the polarization ellipse. 结果以偏振椭圆的形式绘制。
#
# Input properties
# f: frequency of interest
# Gn,Gm: grating order of interest (Gn,Gm)
# make plots: 1 to make plots, 0 otherwise
#
# Output properties 
# major_angle: angle of major axis of polarization ellipse
# ratio: length of major axis divided by length of minor axis of ellipse
#
# Tags: far field polarization ellipse grating
# 远场偏振椭圆光栅
# Copyright 2012 Lumerical Solutions Inc
##############################################

# simplify input variable names by removing spaces
make_plots = %make plots%;

  # find frequency closest to that specified
# by the user
# 找到最接近指定频率的频率
# 由用户
f_vec=getdata("field","f"); 
fi=find(f_vec,f);                  


# Do grating calculation, and separate
# into each field component
# 进行光栅计算，并分离进入每个场分量
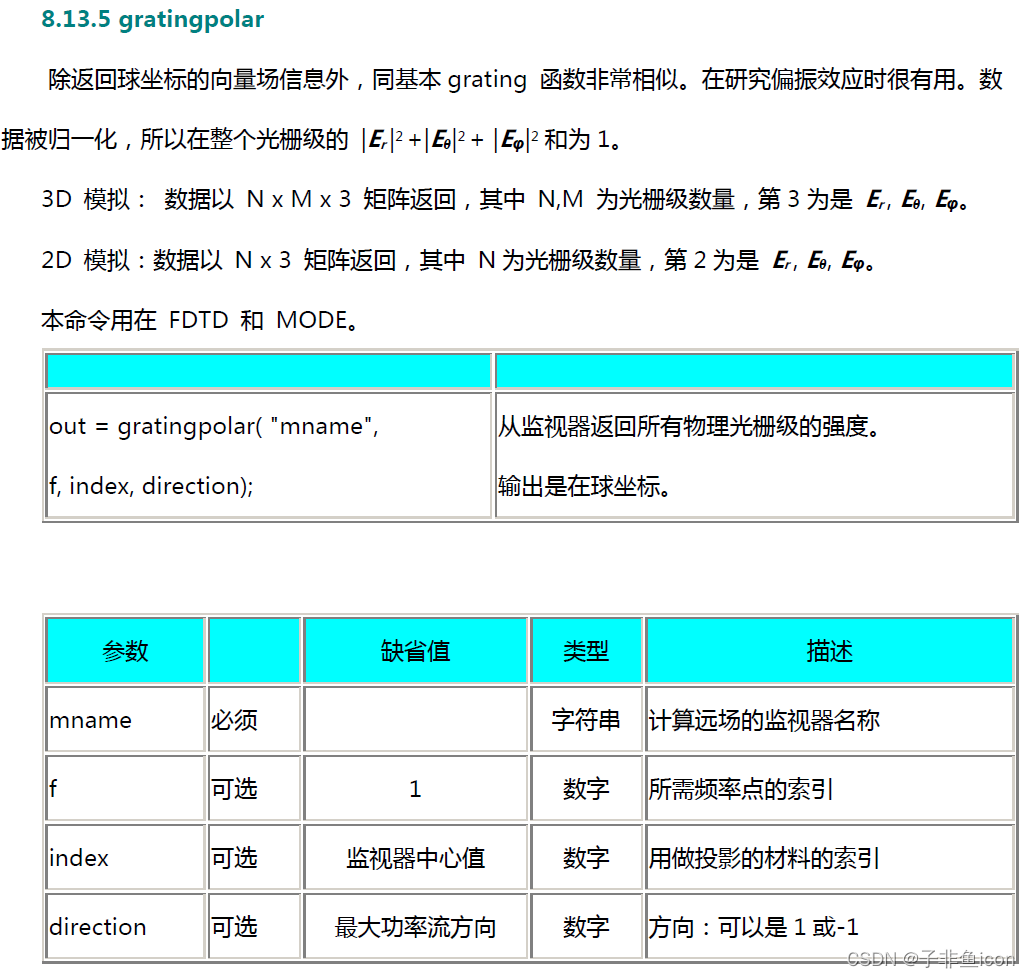
G_vec = gratingpolar("field",fi);# 返回球座标的向量场信息
n = gratingn("field",fi); # 返回第一维级的级数
m = gratingm("field",fi); # 返回第二维级的级数
# n和m都是0
ux= gratingu1("field",fi);
uy= gratingu2("field",fi);
Gtheta = pinch(G_vec,3,2); # 相当于只取了第二种值的所有信息，也就是theta
Gphi   = pinch(G_vec,3,3);
G=abs(Gtheta)^2+abs(Gphi)^2;      # grating order strength


# find index of selected grating order 查找所选光栅阶次的索引
ni = find(n,Gn);
mi = find(m,Gm);

# convert spherical coordinates polarization into 
# S,P polarization and select grating order
# 将球坐标偏振转换为 S,P 偏振并选择光栅阶数
Gs=Gphi(ni,mi);
Gp=Gtheta(ni,mi);

# Calculate polarization ellipse 计算极化椭圆
kappa = linspace(0,360,400)*pi/180;
Gs = real( Gs*exp(1i*kappa) );
Gp = real( Gp*exp(1i*kappa) );

# measure parameters from ellipse 从椭圆测量参数
diameter = sqrt( (Gs)^2+(Gp)^2 );
major_axis = max( diameter);
minor_axis = min( diameter );
ratio = major_axis/minor_axis;

pos_major = find(diameter,max(diameter));
major_angle = atan2(Gs(pos_major),Gp(pos_major))*180/pi;
if(major_angle < -90) { major_angle = major_angle+180; }
if(major_angle > 90) { major_angle = major_angle-180; }
# 把角度限制在-90-90之间

Gs=Gs/major_axis;
Gp=Gp/major_axis;

theta0 = acos(sqrt(1-ux(ni)^2-uy(mi)^2))*180/pi;
phi0 = atan2(uy(mi),ux(ni))*180/pi; 


if (make_plots) {
  # plot grating order strenghts
  image(n,m,G ,"Grating number n","Grating number m","Grating order strength");


  # plot ellipse, and ellipse parameters
  plot(Gp,Gs,"P","S","polarization ellipse (N,M)=("+num2str(Gn)+","+num2str(Gm)+")" +endl+
                       "(theta,phi)=("+num2str(theta0)+","+num2str(phi0)+")" +endl+
                       "axis ratio = " + num2str(ratio) +endl+
                       "major axix angle = "+num2str(major_angle)  );
  setplot("x min",-1); # 设置图形属性
  setplot("x max", 1);
  setplot("y min",-1);
  setplot("y max", 1);
}

gratingpolar及相关函数

在这里插入图片描述

在这里插入图片描述

linspace

索引用kappa(1)，或者kappa(1:6)，kappa(1:2:6).

li*kappa的效果是把kappa的数据写到虚部，比如1变成0+1i

atan2
在这里插入图片描述
atan2()是对象限敏感的，因此需要两个参数

image
在这里插入图片描述
endl

1.1.6 sweep
在这里插入图片描述

1.2 结果

我们将查看两种 LC 方向的结果：第一种是 LC 导向器指向 z 轴（theta = 0，phi = 0），第二种是导向器指向 y 轴（theta = 90° , phi = 0)。在第一种情况下，沿 x 和 y 方向偏振的光仍将以相同的速度传播，因此我们看不到输出光的偏振有任何变化。在第二种情况下，在 y 方向上偏振的光将以与 x 不同的速度传播，我们将看到由于两个分量之间的相位差异而导致的偏振变化。该相位差与 LC 层的厚度成正比：

在这里插入图片描述
分析组绘图结果：

为了确定将偏振改变 90 度（即从 45 度到 -45 度）所需的最佳厚度，我们建立了一个参数扫描项目，将 LCD 层的厚度从 2 到 3 微米扫描，并跟踪椭圆率ellipticity （即长轴和短轴之间的比率）作为这种变化的函数。参数sweep的结果如下图（在sweep项目上右击，选择Visualize-ratio可以看到）。我们可以看到最佳厚度在2.75um左右。

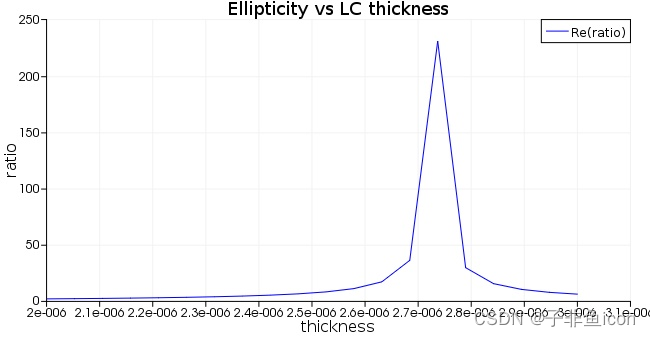
在这里插入图片描述
这也是对于 $\Delta\theta=\pi$ 所期待的结果，因为， $h=\frac{\lambda}{2\Delta n}=2.75\mu m$ .

PS：45度到-45度，难道不是应该90度， $\frac{\pi}{2}$ 吗

还有这里这个 $\Delta n=0.1$ ，查了查应该是双折射率差，1.6-1.5=0.1

二、螺旋扭曲液晶的偏振特性

在本例中，我们将对扭曲向列 LCD (TN-LCD) 进行建模。对于简单的单轴 LCD，请参阅简单 LCD。

在这里插入图片描述

2.1 模拟设置

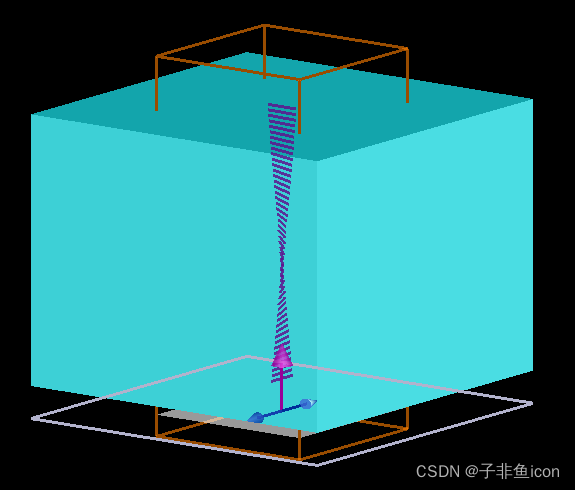
当 TN-LCD 上没有施加电压时，液晶以扭曲配置取向，并且 LC 导向器从 LC 层的底面到顶部均匀地旋转 90 度。由于光以平行于底部导向器（本例中的 x 轴）的偏振进入 LC，光的线性偏振将大致跟随导向器的旋转，因此透射的光将在 y 方向上偏振.当施加电压时，外电场迫使 LC 指向矢变得均匀且平行于传播方向，光的偏振态不会发生变化。

为了模拟 FDTD 中 LC 方向的 90 度扭曲，我们将使用各向异性材料与 LC 导入网格属性相结合。脚本 LCD_twist.lsf 设置螺旋扭曲配置中的 LC 方向，如文件 LCD_twist.fsp 中所示。我们从与底部 LC 导向器（沿 x 轴）具有相同偏振的平面波源开始，并使用 2D DFT 监视器跟踪光在传播通过 TN-LCD 时的偏振变化。

2.1.1 材料设置

各向异性材料和网格属性设置
在这里插入图片描述
这个LC attribute跟上一个案例的设置截面又不一样了

在这里插入图片描述

2.1.2 光源

550nm输入
在这里插入图片描述

2.1.3 脚本 LCD_twist.lsf

# delete existing attribute
select('LC attribute');
delete;  # 删除所选择的实体对象

# define x/y/z
x = 0;
y = 0;
z = linspace(0e-6,5e-6,100);

X = meshgrid3dx(x,y,z);
Y = meshgrid3dy(x,y,z);
Z = meshgrid3dz(x,y,z);
n = matrix(length(x),length(y),length(z),3); # 初始化一个矩阵

# define the orientation function 定义方向函数
n(1:length(x),1:length(y),1:length(z),1) = cos(Z*pi*1e5);
n(1:length(x),1:length(y),1:length(z),2) = sin(Z*pi*1e5);
n(1:length(x),1:length(y),1:length(z),3) = 0;

# create dataset containing orientation vectors and position parameters
# # 创建包含方向向量和位置参数的数据集
LC=rectilineardataset("LC",x,y,z);
LC.addattribute("u",n);

# add LC import grid attribute 添加 LC 导入网格属性
addgridattribute("lc orientation",LC); # lc orientation在attribute下拉栏里
setnamed("LC attribute","nz",50); # set resolution 设置分辨率

2.1.3.1 meshgrid3dx
在这里插入图片描述
2.1.3.2 rectilineardataset

2.1.3.3 addattribute

在这里插入图片描述
2.1.3.4 addgridattribute

2.2 结果

在这里，我们可以通过 TE 分数定义极化（沿 z 的每个点）：

$\frac{|Ex|^2}{|Ex|^2+|Ey|^2}$

脚本 LCD_twist_analysis.lsf 绘制了 TN-LCD 层中的“TE 分数与 z”：

在这里插入图片描述
实际操作时，TN-LCD层会夹在两个偏光片之间（偏光差为90度）。在没有外部场的情况下，光线将在 LCD 层中发生 90 度的偏振变化，因此将被允许通过顶部偏振器（因此处于“开启”状态）。当施加外场时，晶体将与场对齐，因此入射光的偏振不会发生变化，顶部偏光片将不允许任何光通过（因此“关闭” 状态）。

2.2.1 field的结果

Ex随着z的增加，而逐渐减小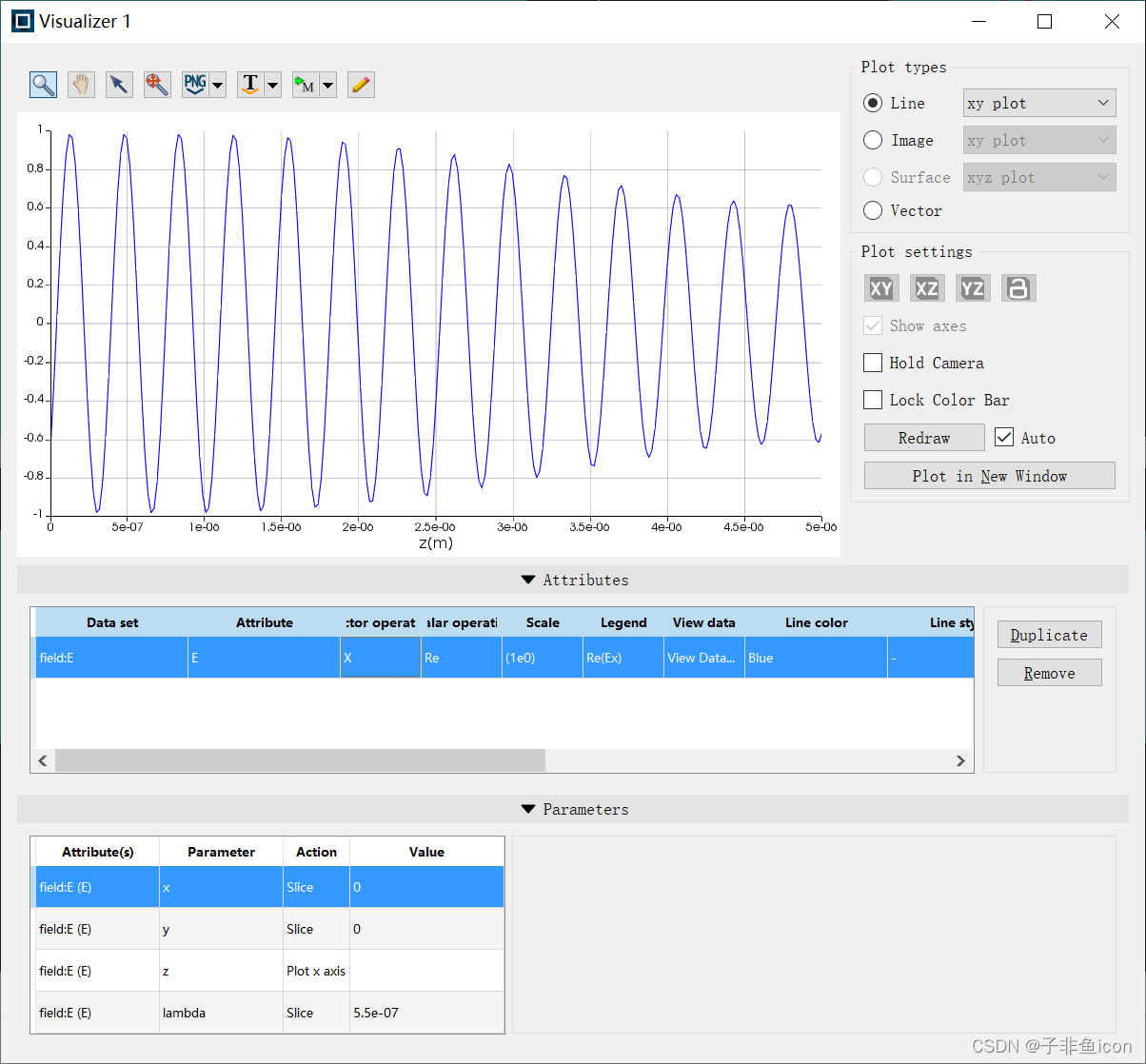在这里插入图片描述

Ey随着z的增加，而逐渐增大

在这里插入图片描述

2.2.2 脚本 LCD_twist_analysis.lsf

closeall;
clear;

E = getresult('field','E');
Ex = E.Ex;
Ey = E.Ey;
z = E.z;

# track the TE fraction in side the rotator 跟踪旋转器侧的 TE 分数
TE_frac = matrix(length(z));
for (i=1:length(z)){
  Ex_slice = pinch(Ex,3,i);
  Ey_slice = pinch(Ey,3,i);
  TE_frac(i) = abs(Ex_slice)^2/(abs(Ex_slice)^2+abs(Ey_slice)^2);
}
# plot results
plot(z*1e6,TE_frac,'z (um)','TE Fraction');