最小生成树的基础应用

注意

最小生成树一般是作用于无向图上的；

Prim&Kruskal的一个核心思想

Prim是每次选择距离最近的边，然后加进来；

Kruskal是将边权升序排序，每次连接两个不连通的点；

---

那如何证明这样选择边是正确的？

这两个算法的证明思路都是一样的；

假设不选当前这条边，最终得到了一棵树，我们将当前这条边加上，必然会形成环；在这个环上，一定可以找出一条长度不小于(因为按两个算法，我们这条边都是最小的)当前边的边，我们用当前这条边去替换找到的这条边，结果一定不会变差(最坏不变，可能变小)；

例题

Kruskal适用于稀疏图，Prim适用于稠密图；

局域网

传送门

题面

思路

注意这句话，两台计算机之间最多只会存在一条连接。

也就是说，可能有多个连通块；

先考虑一个连通块，因为连通块彼此之间是互不干扰的，有多个我们就重复求多个即可；

要删除的最大，也就是保留的最小，也就是求最小生成树；

然而这题因为有多个连通块，我们要求一个"最小生成森林"；

---

Kruskal有一个很好的性质，你求一小段，也是保证正确的；

也就是说，我们最终并不需要让整个图连通起来，在这个过程中，每个连通块内就求出最小生成树了；

也就是像一个进度条一样，求到多少就正确多少了；

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e2 + 10;
struct Edge{
    int u,v,w;
}e[N << 1];
int p[N];
int find(int x){
    if(x == p[x]) return x;
    return p[x] = find(p[x]);
}
void solve(){
    int n,m;
    cin >> n >> m;
    for(int i=1;i<=n;++i) p[i] = i;
    for(int i=1;i<=m;++i){
        int u,v,w;
        cin >> u >> v >> w;
        e[i] = {u,v,w};
    }
    sort(e+1,e+1+m,[](Edge p,Edge q)->bool{
        return p.w < q.w;
    });
    int ans = 0;
    for(int i=1;i<=m;++i){
        int u = e[i].u,v = e[i].v,w = e[i].w;
        int pu = find(u),pv = find(v);
        //merge
        if(pu != pv){
            p[pu] = pv;
        }
        else{
            //求最小生成树是在上面加
            //这题直接在这里加即可；
            //或者求出总权值 - 最小生成树的也可
            ans += w;
        }
    }
    cout << ans << '\n';
}

signed main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

繁忙的都市

传送门

题面

思路

由题干我们可以看出，这题是求一个另类的最小生成树；

要求最大边权最小；

我们发现$Kruskal$的流程用到本题上也是符合的；

因为边权是升序排序的，如果两个点之间是不连通的，那么假设当前边为$u$，我们不选择$u$，而选择后面的某条边$v$使得这两个点之间连通；

我们发现，我们用$u$去替换$v$结果只可能最好(最大的边权可能变小，且仍然连通)；

因此本题启发我们Kruskal不仅可以求传统意义上的最小生成树，也可以求最大边权最小的最小生成树；

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e4 + 10;
struct Edge{
    int u,v,w;
}e[N];
int p[N],sz[N];
int find(int x){
    if(x == p[x]) return x;
    return p[x] = find(p[x]);
}
void merge(int pu,int pv){
    p[pu] = pv;
}
void solve(){
    int n,m;
    cin >> n >> m;
    for(int i=1;i<=n;++i) p[i] = i;
    for(int i=1;i<=m;++i){
        int u,v,w;
        cin >> u >> v >> w;
        e[i] = {u,v,w};
    }
    sort(e+1,e+1+m,[](Edge p,Edge q)->bool{
        return p.w < q.w;
    });
    int ans;
    for(int i=1;i<=m;++i){
        int u = e[i].u,v = e[i].v,w = e[i].w;
        int pu = find(u),pv = find(v);
        if(pu == pv) continue;
        merge(pu,pv);
        ans = w;
    }
    cout << n-1 << ' ' << ans << '\n';
}

signed main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

联络员

传送门

题面

思路

这题已经连接上了一些边(必选)；

我们可以将这些连通块看成一个点，剩下可选的边看成是连通块之间的边，随后在新的图（看成新的点以后）上跑的图跑最小生成树即可；

现在考虑代码怎么写，最小生成树分为Prim和Kruskal；因为我们有一个缩点的过程(将连通块看成新的点)，我们知道并查集的一个集合只有一个唯一的代表元素，这就启发我们使用Kruskal来做；

只需要将必选的边这种关系提前搞好并查集即可；

随后就是常规的Kruskal了；

---

这题和上面局域网的思路中的进度条刚好是互补的；

在那题中，Kruskal只做前面一部分，是正确的；

在本题中，我们知道了Kruskal只做后一部分也是正确的，如下图；

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e4 + 10;
struct Edge{
    int u,v,w;
}e[N];
int p[N];
int find(int x){
    if(x == p[x]) return x;
    return p[x] = find(p[x]);
}
void merge(int pu,int pv){
    p[pu] = pv;
}
int cnt;
void solve(){
    int n,m;
    cin >> n >> m;
    for(int i=1;i<=n;++i) p[i] = i;
    int ans = 0;
    for(int i=1;i<=m;++i){
        int p,u,v,w;
        cin >> p >> u >> v >> w;
        if(p == 1){
            ans += w;
            int pu = find(u),pv = find(v);
            if(pu != pv) merge(pu,pv);
        }
        else e[++cnt] = {u,v,w};
    }
    sort(e+1,e+1+cnt,[](Edge p,Edge q)->bool{
        return p.w < q.w;
    });
    for(int i=1;i<=cnt;++i){
        int u = e[i].u,v = e[i].v,w = e[i].w;
        int pu = find(u),pv = find(v);
        if(pu != pv){
            merge(pu,pv);
            ans += w;
        }
    }
    cout << ans << '\n';
}

signed main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}

连接格点

传送门

题面

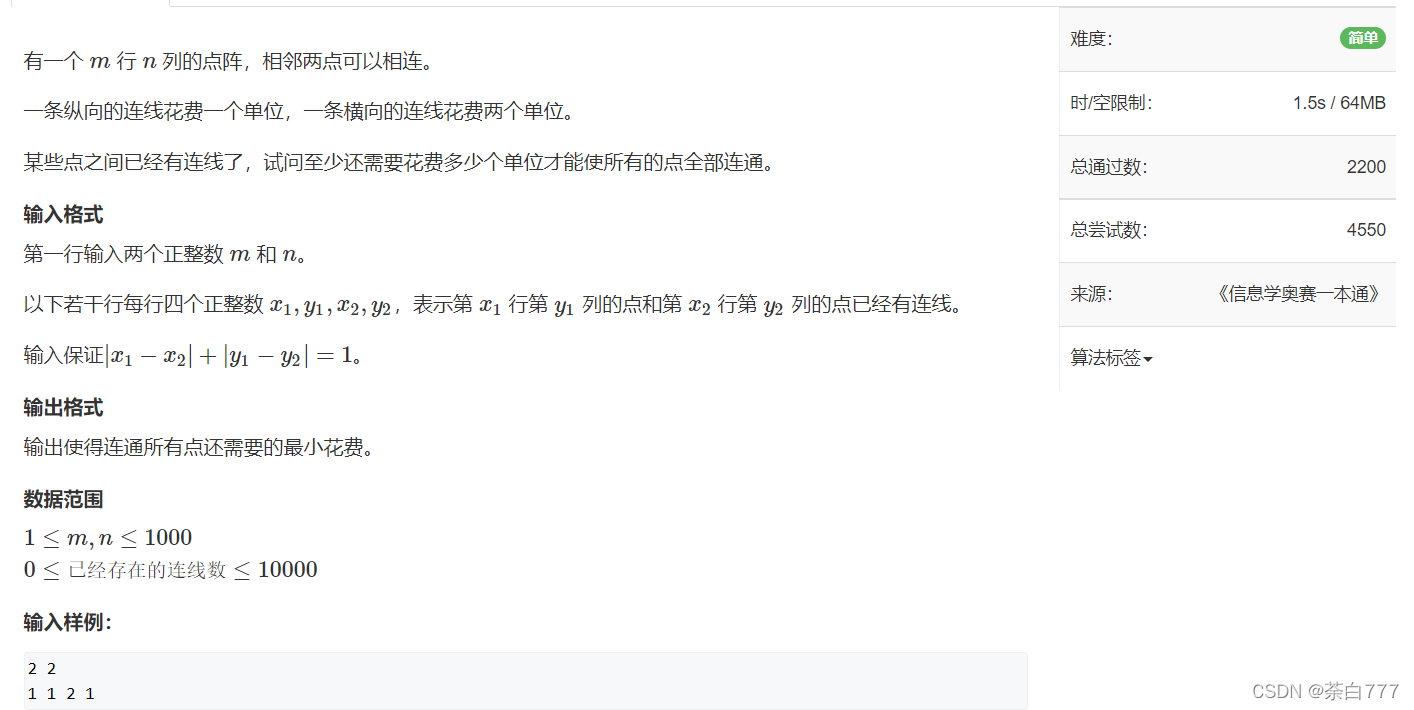
思路

注意这道题的边权都是非负数，如果题目改成这样，那就不是最小生成树的问题了；

因为假设所有的点都连通，并且边权都是负的，那么显然我们应该将所有的边全部选上，因为这样会使得答案更加优秀；

---

因为这题的边权是正的，因此如果边越多那么会使得代价越大，因此边越少越好；

因此我们建个图跑最小生成树即可，思路跟上题是一样的；

这题因为边权只有$1$和$2$，因此我们不需要排序，这样时间就优化成线性的了，先搞纵边再搞横向就行；

---

这题的点数和边数可以用方格去算一下，大致是$10^6$和$2\ast 10^6$；

完全图的话边数是$10^{12}$这个级别的，因此本题还算稀疏图，用Kruskal；

---

在上一题中，我们是只给可选边跑最小生成树；

但是本题中这样做很麻烦，我们又发现如果两个点之前存在必选边，那么这条边在初始化的时候就已经更新到并查集中了；

因此我们哪怕在要跑最小生成树的边中再放入这些必选边也是无所谓的，因为会被continue掉；

这样我们就可以不必考虑过滤这种麻烦事了；

Code

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e3 + 10,M = 1e6 + 10;
struct Edge{
    int u,v,w;
}e[M << 1];
int p[M],n,m;
int find(int x){
    if(x == p[x]) return x;
    return p[x] = find(p[x]);
}
void merge(int u,int v){
    int pu = find(u),pv = find(v);
    if(pu != pv)
        p[pu] = pv;
}
int ids[N][N];//二维坐标转一位
int dx[] = {0,0,1,-1};
int dy[] = {1,-1,0,0};
int dw[] = {2,2,1,1};
int cnt;
void build_edge(){
    //先竖边
    for(int i=1;i<=n;++i){
        for(int j=1;j<=m;++j){
            for(int k=2;k<4;++k){
                int x = i + dx[k],y = j + dy[k],w = dw[k];
                if(x && x <= n && y && y <= m){
                    int u = ids[i][j],v = ids[x][y];
                    if(u < v) e[++cnt] = {u,v,w};
                }
            }
        }
    }
    //再横边
    for(int i=1;i<=n;++i){
        for(int j=1;j<=m;++j){
            for(int k=0;k<2;++k){
                int x = i + dx[k],y = j + dy[k],w = dw[k];
                if(x && x <= n && y && y <= m){
                    int u = ids[i][j],v = ids[x][y];
                    if(u < v) e[++cnt] = {u,v,w};
                }
            }
        }
    }
}
void solve(){
    cin >> n >> m;
    for(int i=1,t=0;i<=n;++i)
        for(int j=1;j<=m;++j)
            ids[i][j] = ++t;
    for(int i=1;i<=n*m;++i) p[i] = i;
    int x1,y1,x2,y2;
    while(cin >> x1 >> y1 >> x2 >> y2){
        int u = ids[x1][y1],v = ids[x2][y2];
        merge(u,v);
    }
    build_edge();
    int ans = 0;
    for(int i=1;i<=cnt;++i){
        int u = e[i].u,v = e[i].v,w = e[i].w;
        if(find(u) == find(v)) continue;
        merge(u,v);
        ans += w;
    }
    cout << ans << '\n';
}

signed main(){
    std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    solve();
    return 0;
}