Energy-efficient Federated Learning via Stabilization-aware On-device Update Scaling 阅读笔记

Energy-efficient Federated Learning via Stabilization-aware On-device Update Scaling

通过支持稳定的设备上更新伸缩实现高效的联邦学习——阅读笔记

本篇文章为论文Energy-efficient Federated Learning via Stabilization-aware On-device Update Scaling阅读笔记

摘要

本篇论文针对联邦学习本地训练的效率优化：

• 联邦学习概述：一种使得多个设备能够在保证数据隐私的同时训练模型。
• 联邦学习缺点：在训练完成之前，在设备上进行了大量的计算密集型迭代，产生大量的能源消耗。随着模型参数的稳定，此类设备训练的迭代逐渐随着时间的推移而逐渐冗余。
• 本篇论文工作：
  • 随时间变化的整数程序（time-varying integer program），但受模型收敛的长期约束。
  • 设计了多项式时间在线算法，该算法基本上平衡了能耗和训练的模型质量。
• 结果：通过严格的证明，我们的方法与最优方法相比只产生次线性（sublinear）遗憾，并保证了相关模型的收敛性。

一、论文背景、动机、主要贡献

1.1 论文背景

​ FL背景介绍：FL是用于隐私保护的分布式学习范例。但是本地训练时涉及进一步的随机梯度下降或者批处理梯度下降，对于worker来说是计算密集的。并且考虑到FL的worker通常是手机、智能家居等电池容量有限的异质设备，对这些设备来说，这样密集的计算产生了大量能源消耗。

论文优化方式：Update Scaling

​ 在边缘网络设备上进行高效节能的联邦学习是非平凡的，而且面临诸多挑战：

• 本地的训练迭代次数与最终模型的质量直接相关

  本地的迭代数量直接关系到最终模型的收敛，节能高效的联邦学习需要在保证模型质量的前提下，减少训练的次数。即，节能的设备上联合学习应该保持梯度不变，同时减少更多的本地训练迭代。

  梯度不变？没懂

• 模型的状态是随着时间变化的，只有在本地训练完成后才能观察到。

  这里的状态包括两个方面：一是梯度的计算需要切实地经过本地训练；二是模型参数难以预估。
  $$难以确定最佳本地培训次数\{\begin{array}{l}梯度无法预估\\ 模型参数无法预估\end{array}$$

• 设备存在异质性进一步提升了减少本地训练次数的困难

​ 最近的工作或没有关注本地优化，关注的或是通信和设备选择；或关注了本地优化，但是对参与者的处理方式没有区别，未能利用来自不同设备的反馈。

1.2 主要贡献

本篇论文具有首创性，主要表现了几点：

• 实验证明了模型参数随时间逐渐稳定
• 制定了一个随时间变化的整数程序，以最大程度地减少设备上的累积能源消耗，但要受到模型结合的长期限制。
• 进行广泛的测试床实验，以评估论文提出的算法，并使用从现实世界中获得的数据集进行评估。

二、论文问题描述和定义

从模型稳定的研究开始。两个目标：

• 何时可以减少迭代次数
• 如何通过缩放来补偿

2.1 Motivation

2.1.1 参数稳定性

​ 随着训练的进行，模型的参数逐渐稳定。在早期，参数变化较大；后期参数较为稳定。两个实验的结果：

2.1.2 通过缩放来近似

​ 当参数逐渐趋于平稳时，每次迭代产生的更新就会变得很小。换句话说，经过两次连续的局部迭代得到的模型随着训练的进行越来越接近。如果一个模型落入另一个模型的近附近，则计算出的梯度可能相似，如下图所示：

​ 重要结论：参数更新与梯度成正比，当每次迭代的梯度往往相似时，只需要执行一部分迭代，其余部分是多余的，以便它们可以删除。

• 完整更新

  一轮完整迭代生成的更新

• 部分更新

  部分迭代相对应的更新称为部分更新

• 缩放更新

  缩放的部分更新称为缩放更新

缩放Scaling的精确定义？

2.1.3 目标和挑战

目标：在保证模型准确度的前提下，减少全局功耗。

问题：

• 有必要弄清减少迭代和扩展更新如何影响全局模型的收敛性

• 本地模型的状态具有时变和不确定性

  因此，只有在本地培训完成后才能观察到本地迭代的冗余，并且很难提前确定最佳的训练配置。

  事后诸葛亮

2.2 系统模型

2.2.1 边缘网络

描述了下面的边缘网络：

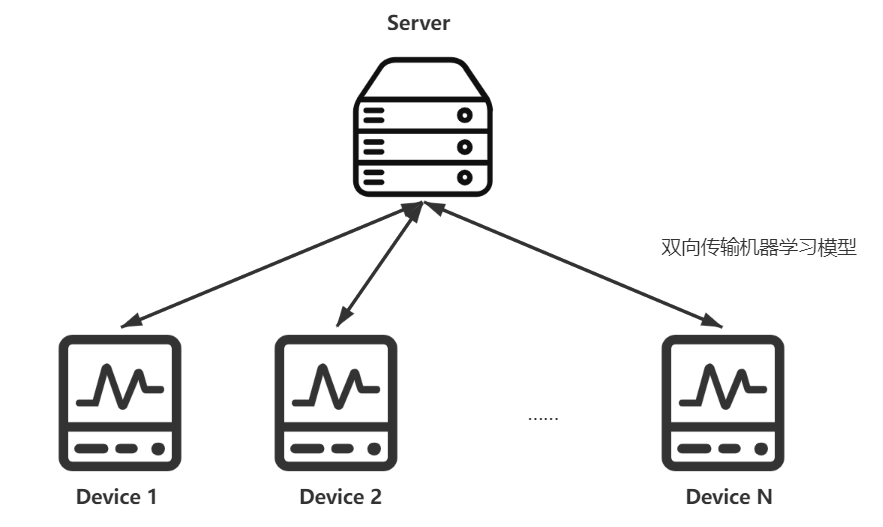
全局目标函数是最小化：

Pd：设备d的训练数据

Fd：设备d的目标函数

2.2.2 联邦学习

​ 论文由于采用了Scaling，故不遵守严格的FedAvg，模型的三个阶段如下：

• 模型准备：服务器广播模型

• 本地训练：使用SGD，随机梯度下降

• 模型聚合：缩放在聚合中，更新模型参数

  

2.2.3 模型收敛

​ 将Scaling Update加入FL。

• 基于一些假设来促进分析：三个假设

• 引理1

  

• 定理1：收敛速度计算

  [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hrYtX9S3-1666515214714)(https://cdn.jsdelivr.net/gh/Holmes233666/blogImage@main/img/image-20221023114446735.png)]

​ 直觉上：较大的训练迭代次数和较小的方差有利于最后模型的质量。由定理1：当参数值逐渐稳定时，方差渐渐变小，可以去掉一些迭代以节能。

2.2.4 能量损耗

​ 本地训练中的消耗包括两个部分：

• 计算消耗：若干轮迭代
• 等待消耗：模型需要聚合，需要等较慢的设备完成

2.3 问题公式化

建立优化问题模型：
P 1 : min ⁡ ∑ t = 1 T ( E t c + E t w )  s.t.  1 T 2 ∑ t = 1 T ∑ d = 1 N p d 2 σ t , d 2 x t , d ≤ ϵ ,  ( 5 )  var.  x t , d ∈ { 1 , … , S } , ∀ t , d , ( 6 ) \begin{aligned} &\mathscr{P}_1: \quad \min \sum_{t=1}^T\left(E_t^{\mathrm{c}}+E_t^{\mathrm{w}}\right)\\ &\text { s.t. } \frac{1}{T^2} \sum_{t=1}^T \sum_{d=1}^N \frac{p_d^2 \sigma_{t, d}^2}{x_{t, d}} \leq \epsilon \text {, }(5)\\ &\text { var. } \quad x_{t, d} \in\{1, \ldots, S\}, \forall t, d ,(6)\end{aligned} ​P1​:mint=1∑T​(Etc​+Etw​) s.t. T21​t=1∑T​d=1∑N​xt,d​pd2​σt,d2​​≤ϵ, (5) var. xt,d​∈{1,…,S},∀t,d,(6)​
约束（5）保证模型的收敛性，其中$ϵ$是模型质量

约束（6）限制决策变量的域

解决${\mathcal{P}}_1$的直接挑战是获得${\sigma }_{t,d}^2$的确切值，该值需要计算所有微型批次的随机梯度。

即要计算完所有的批次，才能获得该数据；而我们的目标是减少批次。

​ 为了解决这个问题，利用引理1在训练过程中实时估计${\sigma }_{t,d}^2$的上限。具体的，将${\sigma }_{t，d}^2$替换为${\hat{\sigma }}_{t，d}^2$，其中${\hat{\sigma }}_{t，d}^2$定义为：

​ 经过一些整合，模型重新转换为：
x t = [ x t , 1 ; … ; x t , d ] , X = { 1 , … , S } d f t ( x t ) = E t c + E t w , h t ( x t ) = ∑ d = 1 N p d 2 σ ^ t , d 2 x t , d − ϵ T . \begin{aligned} &\boldsymbol{x}_t=\left[x_{t, 1} ; \ldots ; x_{t, d}\right], \mathcal{X}=\{1, \ldots, S\}^d \\ &f_t\left(\boldsymbol{x}_t\right)=E_t^{\mathrm{c}}+E_t^{\mathrm{w}}, h_t\left(\boldsymbol{x}_t\right)=\sum_{d=1}^N \frac{p_d^2 \hat{\sigma}_{t, d}^2}{x_{t, d}}-\epsilon T . \end{aligned} ​xt​=[xt,1​;…;xt,d​],X={1,…,S}dft​(xt​)=Etc​+Etw​,ht​(xt​)=d=1∑N​xt,d​pd2​σ^t,d2​​−ϵT.​
Here $f_t$ corresponds to the objective function of ${\mathcal{P}}_1$, and $h_t$ corresponds to Constraint (5). Then, ${\mathcal{P}}_1$ is reformulated as:
$${\mathcal{P}}_2:\underset{{\mathbf{x}}_t\in \mathcal{X},\forall t}{\min }\sum _{t=1}^T{f}_t\left({\mathbf{x}}_t\right)\text{ s.t. }\sum _{t=1}^T{h}_t\left({\mathbf{x}}_t\right)\le 0.$$
${\mathcal{P}}_2$还是非平凡的，经过这样的转换还是存在一些问题：

• 在线的不稳定性

  直到第t轮，${\hat{\sigma }}_{t，d}^2$是未知的，这就意味着得每轮做实时决策。由于${\mathcal{P}}_2$是依赖于时间的，实时决策不可行。

• ${\mathcal{P}}_2$本身求解起来较为棘手

  属于Integer凸面编程，NP-Hard

三、算法设计

​ 本节为多项式在线算法的设计。算法由两个子例程组成：

​ 第一个子例程利用在线学习框架仅基于观察到的信息，以在线方式生成放松问题（relaxed problem）的真实决策。第二个子例程随机将真实决策随机解决，以保留预期的性能。

3.1 放松Relaxation

​ 为了减少问题的难度，通过删除完整性约束来放松问题。${\mathcal{P}}_2$转换为${\mathcal{P}}_3$：

引理：${\mathcal{P}}_3$是凸优化问题

3.2 在线学习例程

​ 利用OCO将问题在线分解为一系列的子问题。OCO强调减少能耗。因此，它在节省能源和提高准确性之间取得了平衡。

3.3 随机舍入子例程

​ 在线学习子例程为每轮生成真实决策，应将其转换为整数决策。

3.4 空灵算法Ethereal Algorithm

​ 结合在线学习子例程和随机舍入子例程，提出空灵算法。在每一轮中，首先要观察到能耗和模型质量。之后，为下一轮准备了真实的决定和虚拟队列。

四、总结

理论分析省略。主要两个工作：

• 随时间变化的整数程序
• 多项式时间在线算法