C/C++各数据类型大小和取值范围
| 类型名称 | 字节数 | 取值范围 |
|---|---|---|
| signed char | 1 | -2^7(-128) ~ 2^7-1(127) |
| unsigned char | 1 | 0 ~ 2^8-1(255) |
| short int 或 short | 2 | -2^15(-32 768) ~ 2^15-1(32 767) |
| unsigned short int 或 unsigned short | 2 | 0 ~ 2^16-1(65 535) |
| int | 4 | -2^31(-2 147 483 648) ~ 2^31-1(2 147 483 647) |
| long int 或 long | 4 | -2^31(-2 147 483 648) ~ 2^31-1(2 147 483 647) |
| unsigned int | 4 | 0 ~ 2^32-1(4 294 967 295) |
| unsigned long int 或 unsigned long | 4 | 0 ~ 2^32-1(4 294 967 295) |
| unsigned long long int 或 unsigned long long | 8 | 0 ~ 2^64-1(1.844674407371e+19) |
| long long int 或 long long | 8 | -2^63(-9.2233720368548e+18) ~ 2^63-1(9.2233720368548e+18) |
上面的简单,就是一个字节站8位,若占n个字节
无符号的就是
2
n
2^n
2n
有符号的把最前面一位拿出来,0代表+,1代表-,
±
2
n
−
1
±2^{n-1}
±2n−1
| 类型名称 | 字节数 | 取值范围 |
|---|---|---|
| float | 4 | ± 3.4 ∗ 1 0 38 ±3.4*10^{38} ±3.4∗1038(精确到6位小数) |
| double | 8 | ± 1.7 ∗ 1 0 308 ±1.7*10^{308} ±1.7∗10308(精确到15位小数) |
| long double | 12 | ± 1.19 ∗ 1 0 4932 ±1.19*10^{4932} ±1.19∗104932(精确到18位小数) |
float和double的精度和取值范围计算方法
float存储方式
首先我们知道常用科学计数法是将所有的数字转换成
(
±
)
a
.
b
∗
1
0
c
(±)a.b*10^c
(±)a.b∗10c 的形式,其中a的范围是1到9共9个整数,b是小数点后的所有数字,c是10的指数。
而计算机中存储的都是二进制数据,所以float存储的数字都要先转化成
(
±
)
a
.
b
∗
2
c
(±)a.b*2^c
(±)a.b∗2c
由于二进制中最大的数字就是1,所以表示法可以写成 ( ± ) 1. b ∗ 2 c (±)1.b *2^c (±)1.b∗2c 的形式,float要想存储小数就只需要存储(±),b和c就可以了。
float的存储正是将4字节32位划分为了3部分来分别存储正负号,小数部分和指数部分的:
- Sign(1位):用来表示浮点数是正数还是负数,0表示正数,1表示负数。
- Exponent(8位):指数部分。即上文提到数字c,但是这里不是直接存储c,为了同时表示正负指数,这里实际存储的是c+127。
- Mantissa(23位):尾数部分。也就是上文中提到的数字b。
float单精度浮点数的二进制表示时 指数为什么要加上127的偏移量?
计算机表示单精度浮点数时,是用8位去存储指数部分,在数值上面,表示 0 − 255 0 -255 0−255,但是我们同样需要有负指数,这就需要拿出一位来表示符号位,这样就变成了 − 127 − 128 -127-128 −127−128。但我们不想要符号位,储存时候会加上127,这样就刚刚好是0~255,就能很好的储存了,在编译时再做个转化就完事了,不然,不移量的话需要判断符号位来判断数值的正负。
例子
以数字6.5为例,看一下这个数字是怎么存储在float变量中的:
-
先来看整数部分,模2求余可以得到二进制表示为110。
-
再来看小数部分,乘2取整可以得到二进制表示为.1(如果你不知道怎样求小数的二进制,请主动搜索一下)。
-
拼接在一起得到110.1然后写成类似于科学计数法的样子,得到 1.101 ∗ 2 2 1.101 * 2^2 1.101∗22
-
从上面的公式中可以知道符号为正,尾数是101,指数是2。
符号为正,那么第一位填0,指数是2,加上偏移量127等于129,二进制表示为10000001,填到2-9位,剩下的尾数101填到尾数位上即可
| S | E | E | E | E | E | E | E | E | M | M | M | M | M | M | M | M | M | M | M | M | M | M | M | M | M | M | M | M | M | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
float最值计算
前面知float存储的数字可以写成 ;当b和c最大时候就是float的取值范围。
指数c,指数位数为11111111最大,因为这个数有特殊用途,所以要减去1得11111110
尾数b,可知当b全为1时,11111111111111111111111
此时为最大取值范围。
借助进制转换器:https://www.sojson.com/hexconvert.html
- 1.b = 1.11111111111111111111111 十进制表示为:1.9999998807907104
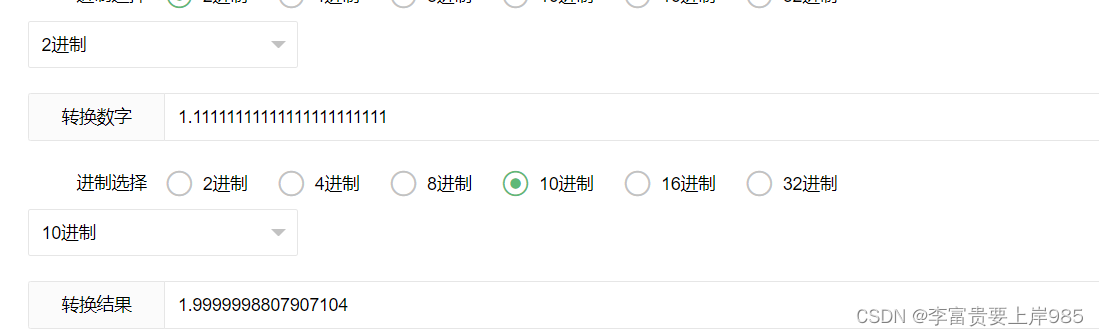
- ∵ c+127 = 11111110 = 256 ∴ c = 127

加上前面的符号位就是
±
3.4
∗
1
0
38
±3.4*10^{38}
±3.4∗1038
double一个意思,自行计算




























 5048
5048

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










