塔防游戏--2021Robocom复赛

题目:

有一种简单的塔防游戏是这样的：给定一张由 n 行 m 列个方格子构成的地图，玩家可以任选一个格子放置自己的大本营，还可以在任意一个格子里放置自己的防御堡垒。大本营和每个防御堡垒都有自己的防御能力值 d，表示可以抵御 d 个僵尸的攻击。每一轮游戏开始时，玩家在规定时间内将本级别可以用的防御堡垒布置在地图中，然后僵尸们就从地图边界涌入地图中，向着大本营发起攻击。每轮进攻持续一个固定的时长，结束后剩余的僵尸就原地蒸发。

每队僵尸可以向一个方格的上下左右四个方向移动。如果相邻的目标方格没有堡垒，它们就可以用 1 秒的时间移动过去，否则会被堡垒阻挡或者消灭。对每一队僵尸（从同一地点出发的所有僵尸）而言，每秒会被堡垒消灭 1 个队友，同时消耗掉该堡垒 1 个单位的防御能力。当防御能力降为 0，则该堡垒消失，剩下的僵尸则用 1 秒移动到这个方格继续行进。注意：如果有多支僵尸队都进入了同一个方格，它们并不会合并成一支队伍。

所有的僵尸队都会根据进攻开始时的地图选择被歼灭最少的到达大本营的路线，并且一直按照这个路线行进，中途不因为地图状态的改变而改变。当这样的进攻路径不唯一时，选择能最快到达大本营的路径。题目保证这样的路径所打掉的堡垒的布局是唯一的。

本题就要求你计算出一轮攻击结束时，地图上的布局情况。

输入格式：

输入首先在第一行中给出三个正整数：不超过 100 的 n 和 m，为地图的尺寸；不超过 1000 的 T，为一轮攻击持续的时长。

随后给出 n+2 行，每行给出 m+2 个数字，每行中的数字都用空格分隔，表示攻击开始前地图上的布局。其中第 1 行、第 1 列、第 n+2 行、第 m+2 列是地图边界外僵尸们出发的位置，这些位置上，0 表示没有僵尸，其他正整数表示从该位置出发的僵尸们的数量。而地图中的每个位置上，0 表示没有堡垒，其它正整数表示该位置上堡垒的防御能力值。大本营是一个特殊的建筑，我们用一个负数 −D 表示这里是大本营，其防御能力值为 D。这里的防御值和任一队僵尸的数量都不超过 100。

注意：僵尸不可在地图边界外移动，它们的第一个移动目标必须在地图中，所以四个角落里出现的僵尸可以被忽略，因为它们没有进入地图的途径。

输出格式：

输出 n 行，每行 m 个数字，对应攻击结束后地图上每个方格的状态。状态的表示与输入相同：没有堡垒的地方输出 0，有堡垒的地方输出其剩余防御值，大本营的位置上输出其剩余防御值的负值。

注意每行数字间以 1 个空格分隔，行首尾不得有多余空格。

当大本营被攻陷时，游戏即刻结束。此时应输出结束时的地图状态，并且在最后一行输出一句 Game Over。

输入样例 1：

7 5 17
0 0 0 0 13 0 0
0 0 0 0 0 0 0
0 0 0 8 0 0 0
0 0 0 0 2 1 0
0 0 0 7 5 3 0
8 0 1 4 -10 1 0
0 0 0 3 3 0 0
0 0 8 0 9 0 0
0 0 0 4 0 0 0

输出样例1:

0 0 0 0 0
0 0 8 0 0
0 0 0 2 0
0 0 7 5 0
0 0 0 -1 0
0 0 0 2 0
0 8 0 9 0

样例说明：

地图布局如下图所示。

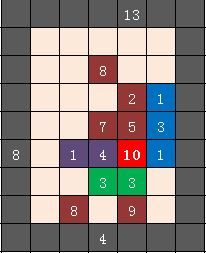
规模为 13 和 8 的两队僵尸都有两种选择，攻打蓝色或者紫色堡垒都是消耗最少的。在这种情况下，规模为 13 的僵尸队走蓝色比较快，需要 1+1+1+2+4+2=11 秒到达大本营边上；规模为 8 的僵尸队走紫色比较快，需要 1+2+5=8 秒到达大本营边上。

规模为 4 的僵尸队比较惨，只能选择绿色堡垒，最后被大本营边上的绿色堡垒消灭。注意到在攻击过程中，其实它们可以等到紫色堡垒被攻陷之后走紫色原始值为 4 的方格，但是因为路径是在初始状态下选定就不能改的，所以它们不能这样选择。

攻打大本营时，规模为 8 的僵尸队剩下了 3 只先到达，在第 11 秒被大本营消灭。此时大本营还剩 7 个单位的防御值，同时规模为 13 的僵尸队剩下的 8 只进入了大本营相邻的方格，开始攻击。但此时距离本轮结束只剩 6 秒，结果大本营在结束时还剩 1 个单位的防御值，玩家胜。

代码:

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <string>
#include <queue>
#include <map>
#include <vector>
#include <cmath>
#include <stack>
#include <utility>
#include <algorithm>
using namespace std;

typedef pair<int,int> PII;
typedef pair<PII,int> PPI;

const int N=105;
int n,m,t;
int sx,sy;
int mp[N][N];
PII ne[N][N];
int dis[N][N];
bool vis[N][N];
vector<PPI> zombie;
int _next[4][2]={{0,1},{1,0},{0,-1},{-1,0}};
typedef struct Node{
	int x,y,w;
	bool operator <(const Node &A)const{
		return w>A.w;
	}
}Node;
priority_queue<Node> pq;
map<PII,vector<int>> ud;
bool judge(int xx,int yy){
	if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&!vis[xx][yy])
		return true;
	return false;
}
void dijkstra(){
	memset(dis,0x3f,sizeof(dis));
	memset(vis,0,sizeof(vis));
	dis[sx][sy]=0;
	pq.push({sx,sy,0});
	while(!pq.empty()){
		Node tmp=pq.top();
		pq.pop();
		int x=tmp.x,y=tmp.y;
		if(vis[x][y])
			continue;
		vis[x][y]=true;
		for(int i=0;i<4;i++){
			int tx=x+_next[i][0];
			int ty=y+_next[i][1];
			if(judge(tx,ty)&&dis[x][y]+mp[tx][ty]<dis[tx][ty]){
				dis[tx][ty]=dis[x][y]+mp[tx][ty];
//				cout<<"("<<tx<<","<<ty<<") ("<<x<<","<<y<<")"<<endl;
				ne[tx][ty]=make_pair(x,y);
				pq.push({tx,ty,dis[tx][ty]});
			}
		}
	}
}
void printMap(){
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			printf("%d",mp[i][j]);
			if(j==m)
				printf("\n");
			else
				printf(" ");
		}
	}
}
int main(){
	scanf("%d%d%d",&n,&m,&t);
	for(int i=0;i<=n+1;i++){
		for(int j=0;j<=m+1;j++){
			scanf("%d",&mp[i][j]);
			if(mp[i][j]<0){
				sx=i,sy=j;
			}
		}
	}
	for(int i=1;i<=n;i++){
		if(mp[i][0]!=0){
			ne[i][0]=make_pair(i,1);
			zombie.push_back(make_pair(make_pair(i,0),mp[i][0]));
		}
		if(mp[i][m+1]!=0){
			ne[i][m+1]=make_pair(i,m);
			zombie.push_back(make_pair(make_pair(i,m+1),mp[i][m+1]));
		}
	}
	for(int j=1;j<=m;j++){
		if(mp[0][j]!=0){
			ne[0][j]=make_pair(1,j);
			zombie.push_back(make_pair(make_pair(0,j),mp[0][j]));
		}
		if(mp[n+1][j]!=0){
			ne[n+1][j]=make_pair(n,j);
			zombie.push_back(make_pair(make_pair(n+1,j),mp[n+1][j]));
		}
	}
	dijkstra();
	bool flag=false;
	for(int i=1;i<=t;i++){
		ud.clear();
		for(int j=0;j<zombie.size();j++){
			if(zombie[j].second==0)
				continue;
			PII nep=ne[zombie[j].first.first][zombie[j].first.second];
			int x=nep.first,y=nep.second;
			if(mp[x][y]==0){
				zombie[j]=make_pair(make_pair(x,y),zombie[j].second);
			}
			else{
				ud[make_pair(x,y)].push_back(j);
			}
		}
		map<PII,vector<int>>::iterator iter=ud.begin();
		for(;iter!=ud.end();iter++){
			int ttx=iter->first.first,tty=iter->first.second;
			for(int j=0;j<iter->second.size();j++){
				
//				cout<<"tt:"<<ttx<<" "<<tty<<endl;
				if(mp[ttx][tty]>0){
					mp[ttx][tty]--;
					zombie[iter->second[j]].second--;
				}
				if(mp[ttx][tty]<0){
					mp[ttx][tty]++;
					zombie[iter->second[j]].second--;
				}
			}
		}
		if(mp[sx][sy]==0){
			flag=true;
			break;
		}
	}
	printMap();
	if(flag)
		printf("Game Over");
}