第五周作业——最大矩形

最大矩形

一、题目
　　给一个直方图，求直方图中的最大矩形的面积。例如，下面这个图片中直方图的高度从左到右分别是2, 1, 4, 5, 1, 3, 3, 他们的宽都是1，其中最大的矩形是阴影部分。

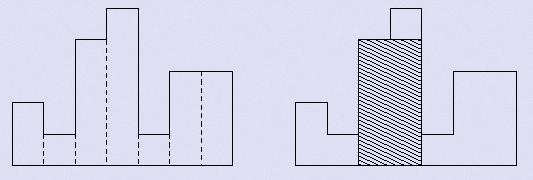
二、输入
　　输入包含多组数据。每组数据用一个整数n来表示直方图中小矩形的个数，你可以假定1 <= n <= 100000. 然后接下来n个整数h1, …, hn, 满足 0 <= hi <= 1000000000. 这些数字表示直方图中从左到右每个小矩形的高度，每个小矩形的宽度为1。 测试数据以0结尾。

三、输出
　　对于每组测试数据输出一行一个整数表示答案。

四、样例输入输出

Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Output

8
4000

五、解题思路
　　单调栈思想。
　　维护一个单调栈，当读入一个比栈尾元素小的元素时，将栈中比它大的元素弹出，再将其入栈，维持栈始终单调递增。初始时读入第一个矩形的高度，之后从左往右逐个读入每个矩形的高度，当读入高度比栈尾元素小时，对栈中比读入元素大的元素进行出栈操作，在出栈时记录当前读入矩形的序号与出栈矩形序号的差值，该值即为出栈矩形往右查找比它高的连续的矩形的数目。之后将矩形的高度数组逆序操作一遍，即可得到每个矩形向左查找的比它高的连续的矩形的数目。这样就可以求出每个矩形左右两边比它高的连续的矩形的数目，乘这个矩形的高度就可以得到面积。求出每个面积后，选出最大的，即为最大矩形的面积。
　　
六、样例代码

#include<stdio.h>
#include<iostream>
using namespace std;
struct point
{
	long long int x,y;
	operator > (const point &p)
	{
		return y > p.y;
	}
}; 

point q[110000];//栈
point a[110000];
point b[110000];

long long int ans1[110000];
long long int ans2[110000]; 
int n;

int main()
{
while(1)
{
    cin>>n;
    if(n==0) break;
    
    for(int i=0;i<110000;i++) //初始化 
    {
    	a[i].x=0;a[i].y=0;
    	b[i].x=0;b[i].y=0;
    	ans1[i]=0;
    	ans2[i]=0;
    	q[i].x=0;q[i].y=0;
	}
    
	for(int i=0;i<n;i++)    //正着存放，倒着存放 
	{
		cin>>a[i].y;
		a[i].x=i;
		b[n-1-i].y=a[i].y;
		b[n-1-i].x=n-1-i;
	} 
	
	q[0]=a[0];
	int r=0;   //栈尾
	
	for(int i=1;i<n;i++)
	{
	    
		if(q[r]>a[i])
		{
			
			while(q[r]>a[i])
			{
				ans1[q[r].x]=i-q[r].x;
				q[r].x=0;
				q[r].y=0;
				r--;
			}
		}
		q[r+1]=a[i];
		r++;		
	}
	
	while(r!=-1) //栈里都弹出 
	{
		ans1[q[r].x]=n-q[r].x;
		q[r].x=0;
		q[r].y=0;
		r--;
	}
	
//	for(int i=0;i<n;i++) printf("%d",ans1[i]);      //结果一 
	
	q[0]=b[0];
	r=0;   //栈尾
	
	for(int i=1;i<n;i++)
	{
	    
		if(q[r]>b[i])
		{
			
			while(q[r]>b[i])
			{
				ans2[q[r].x]=i-q[r].x;
				q[r].x=0;
				q[r].y=0;
				r--;
			}
		}
		q[r+1]=b[i];
		r++;		
	}
	
	while(r!=-1) //栈里都弹出 
	{
		ans2[q[r].x]=n-q[r].x;
		q[r].x=0;
		q[r].y=0;
		r--;
	}	
//	cout<<endl;
//	for(int i=0;i<n;i++) printf("%d",ans2[i]);
	
	
	long long int max=0;
	for(int i=0;i<n;i++)
	{
		long long int s=(ans1[i]+ans2[n-i-1]-1)*a[i].y;
		if(s>max) max=s;
	}
//	cout<<endl;
	cout<<max<<endl;
}	
}