FFT---（递归版和迭代版）( H. Needleand 和H.Rock Paper Scissors)

最新推荐文章于 2023-11-24 13:25:40 发布

axtices

最新推荐文章于 2023-11-24 13:25:40 发布

阅读量981

点赞数 1

分类专栏：数论文章标签：傅立叶分析

本文链接：https://blog.csdn.net/weixin_45819197/article/details/114890441

版权

数论专栏收录该内容

18 篇文章 0 订阅

订阅专栏

文章目录

FFT快速傅里叶变换(加速多项式乘法)

传送门：Rock Paper Scissors

多项式乘多项式常规想法：时间o( $n^2$ ) FFT时间缩减至o( $n l o g n$ );

多项式： $f(x)=a_0x^0+ a_1 x^1 +a_2x^2+........+a_nx^n;$

前置知识

1.点值表示法：f(点，点值) 表示一对

适用 $x_0,f(x_0)),x_1,f(x_1)) ,x_2,f(x_2)) , .......,(x_n,f(x_n)) )$ 就可以完整描述出这个多项式,这就是多项式的点值表示法。

2.多项式相乘

对于 $f (x), g (x)$ 多项式相乘:思路是这样先多项式转为点值表达式，两多项式乘积，再拆解成一项一项。
f[x]= $x_0,f(x_0)),(x_1,f(x_1)) ,(x_2,f(x_2)) , .......,(x_n,f(x_n)) )$
g[x]= $x_0,g(x_0)),(x_1,g(x_1)) ,(x_2,g(x_2)) , .......,(x_n,g(x_n)) )$
f[x]*g[x]= $x_0,f(x_0)*g(x_0)),(x_1,f(x_1)*g(x_1)) ,(x_2,f(x_2)*g(x_2)) , .......,(x_n,f(x_n)*g(x_n)) )$
通过 f[x]*g[x]的点值表达式逆推多项式的系数。

3.欧拉公式

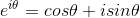
在这里插入图片描述
完美：巧妙将虚数与弧度制关联了。
含义：不难发现：a+bi= $c o s (p)$ +i $s i n (p)$ ; a = $c o s (p)$ b= $s i n (p)$
而且虚数模长刚好是1。对应到坐标系那就是一条与x轴夹角为p的直线！！！。
不难发现： $cos(p)+isin(p) )^2$ = $e^ {2ip}$ = $(c o s (2 * p) + i s i n (2 * p))$
结论：已知p，求np的cos，sin ，就是 $cos(p)+isin(p) )^n$ 分别对应的实数和虚数部分。

4.单位根

首先是一个圆，半径为1。在这里插入图片描述
复数满足 $w^n$ =1称w作是n次单位根. (ps:所以单位根是复数).
将单位圆分成n等分，
单位根就是：( $W_n^0$ ) ( $W_n^1$ )( $W_n^2$ )( $W_n^3$ )…( $W_n^(n-1))$ ).
结合欧拉公式：

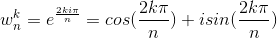
所以本质上单位根也就是模长为夹角为k2(π)/n.
ps:为什么是这样的呢? 圆分成n等分，每等分的角度是：2* $\frac{π}{n}$ 。( $W_n^0$ ) (对应到坐标系是(1,0)) ,( $W_n^1$ ) 对应的直线与x轴的正方向成夹角2* $\frac{π}{n}$ ，( $W_n^2$ ) 22 $\frac{π}{n}$ …以次都是这样的。
单位根性质：
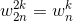
在这里插入图片描述
这个等式也是很好理解的。想成夹角就对了:
第一个夹角2k $\frac{2*π}{2*n}$ 化简就是第二个。

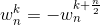
这个也好理解：在原来的夹角添加π，所以实数，虚数去相反数咯。

且满足： $($ W_n^k $^n$ =1；

FFT的实现过程：

FFT就是将系数表示法转化成点值表示法相乘，再由点值表示法转化为系数表示法的过程，第一个过程叫做求值(DFT)，第二个过程叫做插值(IDFT)
设 $A_0$ (X)为x的指数为偶数次的， $A_1$ (X)为x的指数为奇数次的。
可得：
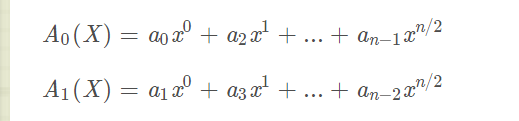
在这里插入图片描述
即得：

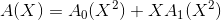
可以发现 $A_0$ ( $X^2$ )与 $A_1$ ( $X^2$ )是两个长度为原来一半的多项式，
然后就分而治之。（两个长度为原来的一半，且长度一样，这点必须，至于为什么
提一下：点值表达式）。
现在就把单位根带进去：
由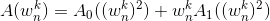：在这里插入图片描述
得到：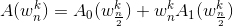
代码先放这：a[i] = a0[i] + w1 * a1[i];
由：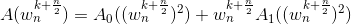
得到：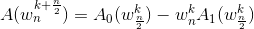
这： a[i + (len >> 1)] = a0[i] - w1 * a1[i];
所以只要考虑1~ $\frac{n}{2}$ 就行了。

a[i] = a0[i] + w1 * a1[i];
       a[i + (len >> 1)] = a0[i] - w1 * a1[i];

ps：蝴蝶变换移位操作 ------以后补

IFFT（逆傅里叶变换） //拆解的过程

我们已经将两个多项式从系数表示法转化成点值表示法相乘后，还要将结果从点值表示法转化为系数表示法，也就是IFFT（快速傅里叶逆变换）

首先思考一个问题，为什么要把
（单位根）作为x代入？
当然是因为离散傅里叶变换特殊的性质，而这也和IFFT有关。

补一个小前置知识： $\displaystyle\sum_{i=1}^{n} a_i^2$ $\displaystyle\sum_{j=1}^{n} b_j^2$ = $\displaystyle\sum_{j=1}^{n} b_j^2$ $\displaystyle\sum_{i=1}^{n} a_i^2$ 方便看懂后面的运算证明。
证明参考：blog
在这里插入图片描述

H. Needleand

题意：三条间距相等的平行直线上各有一些点，在每条直线各选一点，求三点共线的直线条数。

思路：所以我只要a+b=mid*2就行了
a数组的值看成次数，默认的系数为1 b数组也是如此。
因为数组是-30000~30000 所以所有的值都右移动30000用FFT算法求解

代码实现FFT（递归版）: 详解

#include<iostream>
#include<algorithm>
#include<math.h>
#include<cstring>
#include<vector>
#include<queue>
#define ll long long
const double PI = acos(-1.0);
ll gcd(ll a,ll b){ return b? gcd(b,a%b):a;}
const int N=5e5+10;
const ll mod=1e9+7;
ll read(){
    ll s = 0, f = 1; char ch = getchar();
    while(!isdigit(ch)){
        if(ch == '-') f = -1;
        ch = getchar();
    }
    while(isdigit(ch)) s = (s << 3) + (s << 1) + (ch ^ 48), ch = getchar();
    return s * f;
}
using namespace std;
struct zw{
    double x, y; //实数 虚数
    zw(double  a=0 ,double  b=0 ){
        x = a;
        y = b;
    }
}a[N],b[N];
//结构体zw的运算符(- + *)定义. 
zw operator - (zw a, zw b) { return zw(a.x - b.x, a.y - b.y); }
zw operator + (zw a, zw b) { return zw(a.x + b.x, a.y + b.y); }
zw operator * (zw a, zw b) { return zw(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x); }

int n,m,q;
int sum[N];   //存多项式相乘后的结果----系数   eg：sum[6]=12;就是x的6次方的系数是12 
int mid[N];   //存值。 
void ttf(zw *a,int len,int o){  
    //这里的len都是2的次方(必须保证)。这样才能 保证每次分而治之的奇数项和偶数项长度相同。
	//o为1 FFT o为-1 IFFT  
	// o -1 的含义： 前面给出了证明(目录：IFFT) 
   //递归出口
   if(len==1)
       return;
    
   zw a0[len >> 1], a1[len >> 1];//创建偶 奇 次项式 
   //cout<<"usb"<<endl;
   for (int i = 0; i < len; i+=2){
   	
       a0[i >> 1] = a[i]; // 0 2 4 6 8 10  
       a1[i >> 1] = a[i + 1]; // 1 3 5 7 9 11
   }
   //分而治之 
   ttf(a0, len >> 1, o);
   ttf(a1, len >> 1, o);
   //单位角性质
   zw w1 = zw(1, 0);  //初始态 
   zw w0 = zw(cos(2 * PI / len), o * sin(2 * PI / len));
    //欧拉公式。什么意思呢？ 2π分成len份，在这个圆中单位角2*π/len 
   for (int i = 0; i < (len >> 1);i++){
       a[i] = a0[i] + w1 * a1[i]; //A(X)=A0(X^2)+XA1(X^2); 只是这里的x是单位根(见目录单位根详解) 
       a[i + (len >> 1)] = a0[i] - w1 * a1[i];
       w1 = w1*w0; // 有序增加夹角读数 从0 p 2*p 3*P 4*p.....2*π. 
   }
}
int main(){
    
    n = read();
    int ans = 0;
	int maxs=0;//得出a，b数组里最大数 
	int base=30000;
    for (int i = 0; i < n;i++){
        ans = read() + base;
        a[ans].x++;
        maxs = max(maxs, ans);
    }
    m = read();
    for (int i = 0; i < m;i++){
       mid[i]=read()+base;
    }
    q = read();
    for (int i = 0; i < q;i++){
        ans = read() + base;
        b[ans].x++;
        maxs = max(ans, maxs);
    }
    int len = 1;
    for (; len <(maxs<<1);len<<=1)
        ;
        //cout<<len<<endl;
    //进行点值表达式 FFT 
    ttf(a, len, 1);
    ttf(b, len, 1);
    //乘积 -->聚集 也就是g(x)*f(x) 知识这里都是虚数表示。 
    for (int i = 0; i < len;i++){
        a[i] = a[i] * b[i];     //虚数的乘法
    }
    //拆解 IFFT 
    ttf(a, len, -1);
    for (int i = 0; i < len;i++){
    	//浮点四舍五入 转int 
        sum[i] = (int)(a[i].x/len + 0.5);
         //cout<<"i:"<<i<<" "<<sum[i]<<endl;
    }
    ans = 0;
    for (int i = 0; i < m;i++){
        ans += sum[mid[i] << 1];
    }
    cout << ans << endl;
    getchar();
    getchar();
    return 0;
}

--------------------------------------------------------------------蝴蝶变换来啦来啦--------------------------------------------------------------------------------------------

蝴蝶变换:

引入理由：递归版的FFT常数巨大，实现起来比较复杂，于是又有了迭代的写法
前面的递归每层有这样特点：
原数组：(0,1,2,3,4,5,6,7)
step1:(0,2,4,6) (1,3,5,7)
step2: (0,4) (2,6) (1,5) (3,7)
step3: 0 4 2 6 1 5 3 7 （rev数组）
对比原数组和rev数组：每个原数组元素他的二进制颠倒过来就是rev数组。
在这里插入图片描述
观察容易发现: rev[2]右移一位就是rev[4], rev[2]右移一位并加1就是rev[5];
l：二进制位数上图为3.
结论：rev[i]=rev[i>>1]>>1) |((1&i)<<(l-1))。（可证明一般性,感兴趣可以想想~）
(数位dp)
多项式乘法的（次数从0开始）
code: （配有详细解释）
在这里插入图片描述

#include<iostream>
#include<algorithm>
#include<math.h>
#include<cstring>
#include<vector>
#include<queue>
#define ll long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
ll gcd(ll a,ll b){ return b? gcd(b,a%b):a;}
const int N=1e7+10;
const ll mod=1e9+7;
const double PI = acos(-1.0);
ll read(){
    ll s = 0, f = 1; char ch = getchar();
    while(!isdigit(ch)){
        if(ch == '-') f = -1;
        ch = getchar();
    }
    while(isdigit(ch)) s = (s << 3) + (s << 1) + (ch ^ 48), ch = getchar();
    return s * f;
}
using namespace std;
struct zw{
	double r,i;
	zw(double x = 0,double y=0){
		r = x;
		i = y;
	}
}a[N],b[N];
zw operator *(zw x,zw y){
	return zw(x.r * y.r - x.i * y.i, x.i * y.r + x.r * y.i);
}
zw operator +(zw x,zw y){
	return zw(x.r + y.r, x.i + y.i);
}
zw operator -(zw x,zw y){
	return zw(x.r - y.r, x.i - y.i);
}
ll rev[N];
ll n, m,len;
void FFT(zw *a,int len,int o){
	rep(i,1,len-1){
		if(i<rev[i]){
			//蝴蝶变换，二进制颠倒：比如3 ，6 二进制颠倒。。。
			//所以只要变换一次就可以了。
			swap(a[i], a[rev[i]]);
		}
	}
	// h:1, 2, 4 ,8 16
	for (int h = 1; h < len; h *= 2){
		//注意这里PI/h  不是PI*2/h.
		//h的含义即是：奇和偶的项式的个数。
		//因为这是逆操作， 通过奇数(h项式)和偶数项(h)的值，合并求出2*h项式
		//w1：单位角。
		zw w1 = zw(cos(PI / h), o * sin(PI / h));
		for (int j = 0; j < len;j+=2*h){
			//j:0 2 4 6 
			//(0,1) (2,3) (4,5) (6,7)成一对.
			zw w0 = zw(1, 0);
			//j+h 只需要求一半即可。
			for (int k = j; k < j + h;k++){
				//偶数项
				zw x = a[k];
				//奇数项乘以w0  
				zw y = w0*a[k+h];
				a[k] = x + y;
				a[k + h] = x - y;
				w0 = w1 * w0;
			}
		}
	}
	return;
}
int main (){
	n = read();
	m = read();
	//for 循环
	rep(i, 0, n - 1) a[i].r = read();
	rep(i, 0, m - 1) b[i].r = read();
	len = 1;
	int l = 0;
	while(len<(n+m)){
		len <<= 1;
		l++;
	}
	//cout << l << len <<endl;
	//蝴蝶变换
	rep(i,0,len-1){
		//上文已解释
		rev[i] = (rev[i >> 1] >> 1) | ((i & 1) <<(l-1));
	}
	//rep(i, 0, len - 1) cout << rev[i] << " ";
	cout << endl;
	FFT(a, len, 1);
	FFT(b, len, 1);
	rep(i,0,len){
		a[i] = a[i] * b[i];
	}
	FFT(a, len, -1);
	rep(i,0,n+m-2){
		int qs = (int)(a[i].r / len + 0.5);
		cout << qs << " ";
	}
	getchar();
	getchar();
	return 0;
}

来一题：这题特点卡时，如果用FFT的递归版超时。 FFT迭代版可AC~。

传送门：Rock Paper Scissors

题意：原串和模式串，在原串中选出一子串与模式串进行石头剪刀布，希望模式串赢的次数最大。

思路：1.R>S S>P P>R 先将模式串进行预处理：如RRRR ----->SSSS 这样只需要与原串的子串进行相等的匹配即可。
2.那这和多项式又有什么关系呢？预处理的模式串再转一下。如下图：
这样可以得知：多项式相乘后K $x^3$ 的k含义即是：选中原串的子串(下标0~3)与处理后的模式串的成功匹配次数。
3.这里需要三次FFT ，分别是R，S，P处理。
原串的R的系数为1，其余为0。模式串同理。
原串的S的系数为1，其余为0。模式串同理。
原串的P的系数为1，其余为0。模式串同理。
所有第二条还不够准确，成功匹配次数应该是：三次FFT得到的k的和(sum= $k_R$ + $k_S$ + $k_P$ )。然后求出sum的最大值.
在这里插入图片描述
code:

#include<iostream>
#include<algorithm>
#include<math.h>
#include<cstring>
#include<vector>
#include<queue>
#include<set>
#define ll long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
ll gcd(ll a,ll b){ return b? gcd(b,a%b):a;}
const int N=9e5+10;
const ll mod=1e9+7;
const double PI = acos(-1.0);
ll read(){
    ll s = 0, f = 1; char ch = getchar();
    while(!isdigit(ch)){
        if(ch == '-') f = -1;
        ch = getchar();
    }
    while(isdigit(ch)) s = (s << 3) + (s << 1) + (ch ^ 48), ch = getchar();
    return s * f;
}
using namespace std;
struct zw{
    double r;
    double i;  //????
    zw(double a=0,double b=0){
        r = a;
        i = b;
    }
}a[N],b[N],c[N];
zw operator * (zw x,zw y){
    return zw(x.r * y.r - x.i * y.i, x.r * y.i + x.i * y.r);
}
zw operator + (zw x,zw y){
    return zw(x.r + y.r, x.i + y.i);
}
zw operator -(zw x,zw y){
    return zw(x.r - y.r, x.i - y.i);
}
char s[N]; 
char d[N],mo[N];
int sum[N];
int n, m;
int len=1;
int rev[N];
void  FFT(zw *a,int len,int o){
	rep(i,1,len-1){
		if(i<rev[i]){
			swap(a[i], a[rev[i]]);
		}
	}
	for (int h = 1; h < len; h *= 2){
		zw w1 = zw(cos(PI / h), o * sin(PI / h));
		for (int j = 0; j < len;j+=2*h){
			zw w0 = zw(1, 0);
			for (int k = j; k < j + h;k++){
				zw x = a[k];
				zw y = w0*a[k+h];
				a[k] = x + y;
				a[k + h] = x - y;
				w0 = w1 * w0;
			}
		}
	}
	return;
}
//ch: 传入 R S P
void solve(char ch){
	//初始化 
    for (int i = 0; i <len;i++){
        a[i] = zw(0, 0);
        b[i] = zw(0, 0);
        c[i] = zw(0, 0);
    }
    //a原串 
    for (int i = 0; i < n;i++){
        if(s[i]==ch)
            a[i].r = 1;
    }
    //b模式串 
    for (int i = 0; i < m;i++){
        if(mo[i]==ch)
            b[i].r= 1;
    }
    //rep(i,0,m-1) cout<<b[i].r<<" ";cout<<endl;
    FFT(a, len, 1);
    FFT(b, len, 1);
    for (int i = 0; i < len;i++){
        c[i] = a[i] * b[i];
    }
    FFT(c, len, -1);
    for (int i = 0; i<len;i++){
    	//cout<<(int)((c[i].r/len)+0.5)<<" ";
    	//sum=k_R+k_S+k_P  三次 
        sum[i] += (int)((c[i].r/len)+0.5);
    }
   // cout<<endl;
}
int main(){
   
    n = read();
    m = read();
    cin >> s >> d;
    //模式串预处理+反串 
    for (int i = m - 1; i >= 0;i--){
        int j = m - i - 1;
        if(d[j]=='R'){
            mo[i] = 'S';
        }else if(d[j]=='P'){
            mo[i] = 'R';
        }else if(d[j]=='S'){
            mo[i] = 'P';
        }
    }
   // rep(i,0,m-1) cout<<mo[i]<<" ";cout<<endl;
   int l=0;
    for (; len <n + m;len<<=1)
        l++;
    rep(i,0,len-1){
		rev[i] = (rev[i >> 1] >> 1) | ((i & 1) <<(l-1));
	}
   // cout<<len<<endl;
    solve('R');
    solve('S');
    solve('P');
    int ans = 0;
    //得出最大值 
    for (int i = m - 1; i <=n+m-2;i++){
        ans = max(sum[i], ans);
    }
    cout << ans << endl;
    getchar();
    getchar();
    return 0;
}

参考资料：
浅谈 FFT （终于懂一点了~~）
超详细易懂FFT（快速傅里叶变换）及代码实现
 FFT算法讲解——麻麻我终于会FFT了！
从多项式乘法到快速傅里叶变换

axtices

关注

1
点赞
踩
5

收藏

觉得还不错? 一键收藏
打赏
0
评论
FFT---（递归版和迭代版）( H. Needleand 和H.Rock Paper Scissors)

FFT快速傅里叶变换(加速多项式乘法)传送门多项式乘多项式常规想法：时间o(n2n^2n2) FFT时间缩减至o(nlognnlognnlogn);多项式：f(x)=a0x0+a1x1+a2x2+........+anxn;f(x)=a_0x^0+ a_1 x^1 +a_2x^2+........+a_nx^n;f(x)=a0x0+a1x1+a2x2+........+anxn;前置知识1.点值表示法：f(点，点值) 表示一对适用(x0,f(x0)),x1,f(x1)),x2,f(x
复制链接

扫一扫