文章目录
磨磨唧唧写了半个月,想起来就写点喽,ACM必备数论基础知识已全部讲完了,这只是我对数论的总结和理解,发现文章中有错误,可以指正,仅供参考,谢谢。撒花啦。
组合计数
排列数
从 n n n个不同的元素中依次取出 m m m个元素排成一列,产生的不同排列的数量为: A n m A_n^m Anm= n ! ( n − m ) ! \frac{n!}{(n-m)!} (n−m)!n! ###
组合数
从n个不同的元素中取出m个组成一个集合(不考虑顺序),产生不同集合的数量为: C n m C_n^m Cnm= n ! ( n − m ) ! m ! \frac{n!}{(n-m)!m!} (n−m)!m!n!
一些简单性质:
1. C n m = C n n − m C_n^m=C_n^{n-m} Cnm=Cnn−m
2. C n m = C n − 1 m + C n − 1 m − 1 C_n^m=C_{n-1}^m+C_{n-1}^{m-1} Cnm=Cn−1m+Cn−1m−1
3. C n 0 + C n 1 + C n 2 + . . . . . + C n n = 2 n C_n^0+C_n^1+C_n^2+.....+C_n^n=2^n Cn0+Cn1+Cn2+.....+Cnn=2n
多重集的排列数 设 S = S= S={ n 1 ⋅ a 1 , n 2 ⋅ a 2 , n 3 ⋅ a 3 , . . . . . , n k ⋅ a k n_1\cdot a_1, n_2\cdot a_2, n_3\cdot a_3,....., n_k\cdot a_k n1⋅a1,n2⋅a2,n3⋅a3,.....,nk⋅ak}是由 n 1 n_1 n1个 a 1 a_1 a1, n 2 n_2 n2个 a 2 a_2 a2… n k n_k nk个 a k a_k ak组成的多重集。
S S S 的全排列个数为: n ! n 1 ! n 2 ! n 3 ! . . . . n k ! \frac{n!}{n_1!n_2!n_3!....n_k!} n1!n2!n3!....nk!n! 多重集的组合数
这里有一个小小的扩展:在上面的约束条件中再添加选取 a 1 a_1 a1个数不少于 n 0 n_0 n0,并保证 n 0 < r n_0<r n0<r,问可以产生多重集的数量为:
思路: 选取不少于 n 0 n_0 n0 ,意味着什么呢:在插入(k-1)个挡板时有了约束,我们不妨把插完挡板后,
第一个挡板前的元素个数视为从 a 1 a_1 a1选取的个数。
这样就有了 [ n 0 n_0 n0 和 剩下的 ( r − n 0 ) (r-n_0) (r−n0)], 然后挡板要求只能被落在"剩下的 ( r − n 0 ) (r-n_0) (r−n0)"。
这样就满足了选取 a 1 a_1 a1个数不少于 n 0 n_0 n0的约束。
然后就能迎刃而解啦。 ( r − n 0 ) + ( k − 1 ) = r − n 0 + k − 1 (r-n_0)+(k-1)=r-n_0+k-1 (r−n0)+(k−1)=r−n0+k−1
产生多重集的数量是: C r − n 0 + k − 1 k − 1 C_{r-n_0+k-1}^{k-1} Cr−n0+k−1k−1
这个结论在求更为一般的r的情况,会用到。
例题:Counting swaps
传送门
题意:给定一个n的排列P,问进行若干次操作,每次选择两个整数
x
,
y
x,y
x,y交换
P
x
,
P
y
P_x,P_y
Px,Py
问用最少的操作次数将给定排列变成单调上升的序列
1
,
2....
n
1,2....n
1,2....n有多少种方式。对结果
1
e
9
+
9
1e9+9
1e9+9取模。
思路:
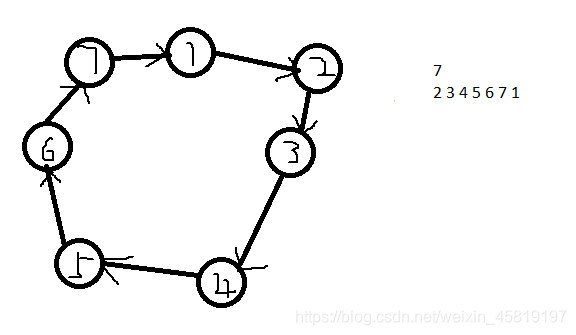
最少操作次数??怎么实现?对于P排列,可以看成一个图。 花出来的图,对于每个点都是入度和出度是1.可知道这个图一定一个环或者多个环。
而且环是一个完整的环,不存在环包含环。而得到单调上升序列,那么图就成了每个点成一个自环。 现在我们需要考虑 原图变成各个点成自环的过程。
两个位置 i , j i,j i,j交换,对图的效果是怎么样的呢。 对没有错, i , j i,j i,j指向的点交换了。 如图:
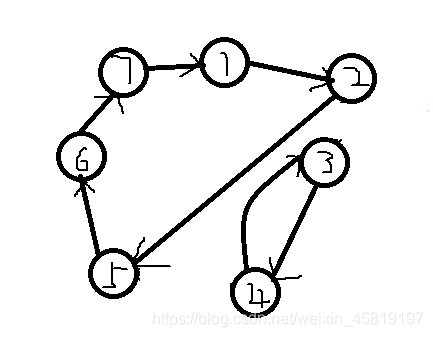
对位置 2 , 4 2,4 2,4交换一下,得到的图是这样的。
这里交换了两个位置,使得一个环变成了两个环。数学归纳法,到最后各个点都成了自环。一个环的点有k个。
那么要交换 k − 1 k-1 k−1次后,k个点成了闭环。(这里可能有人就要问了,为啥我要选一个环上的两点呢,我选不在一个环两个点
进行不行吗?题意有说明,执行交换操作的最小次数,所以我们的操作时要最优的)。
这里我们知道了最少的操作次数,现在我们就来求结果吧。
令一个环长度是n,将该换拆成长度为
x
x
x和
y
y
y的两个环。
那么我们拆成长度
x
,
y
x,y
x,y的环的方式有
n
n
n种。
(
n
−
2
)
!
(
x
−
1
)
!
(
y
−
1
)
!
\frac{(n-2)!}{(x-1)!(y-1)!}
(x−1)!(y−1)!(n−2)!,为啥呢。
x
x
x环,需要交换
x
−
1
x-1
x−1次,
y
y
y环,需要交换
y
−
1
y-1
y−1次,然后现在我们已经具体一种方式了,
在一种具体方式中,就是多重集排列数了。
F
(
n
)
=
n
n
−
2
F(n)=n^{n-2}
F(n)=nn−2我们可以通过打表得到结果。

ACcode
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define ull unsigned long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
ll gcd(ll a,ll b){ return b? gcd(b,a%b):a;}
const int N=2e5+10;
const ll P=1e9+9;
ll read(){
ll s = 0, f = 1; char ch = getchar();
while(!isdigit(ch)){
if(ch == '-') f = -1;
ch = getchar();
}
while(isdigit(ch)) s = (s << 3) + (s << 1) + (ch ^ 48), ch = getchar();
return s * f;
}
using namespace std;
ll qpow(ll a,ll x){
ll ans=1;
while(x){
if(x&1){
ans=(ans*a)%P;
}
x>>=1;
a=(a*a)%P;
}
return ans;
}
ll jie[N],nv[N];
void pre(){
jie[0]=1;
for(int i=1;i<=1e5;i++){
jie[i]=(jie[i-1]*i)%P;
}
}
int a[N];
bool flag[N];
int cnt,c[N];
void solve(){
int n=read();
rep(i,1,n){
a[i]=read();flag[i]=false;
}
cnt=0;
rep(i,1,n){
if(flag[i]==0){
int k=0;
int j=i;
while(flag[j]==0){
flag[j]=1;
k++;
j=a[j];
}
c[++cnt]=k;
}
}
// rep(i,1,cnt){
// printf("%d\n",c[i]);
// }
// f_n=n^{n-2}
ll sum=jie[n-cnt];
rep(i,1,cnt){
// sum=sum*nv[c[i]-1]%P;
sum=sum*qpow(jie[c[i]-1],P-2)%P;
}
rep(i,1,cnt){
if(c[i]==1) continue;
sum=sum*qpow(c[i],c[i]-2)%P;
}
printf("%lld\n",sum);
return ;
}
int main (){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
pre();
int T=read();
while(T--)
solve();
getchar();
getchar();
return 0;
}
Lucas定理 C n m ≡ C n m o d p m m o d p ∗ C n / p m / p ( m o d p ) C_n^m\equiv C_{n\ mod\ p}^{m\ mod\ p}*C_{n/p}^{m/p}(mod\ p) Cnm≡Cn mod pm mod p∗Cn/pm/p(mod p)
若p是质数,则对于任意整数
1
<
=
m
<
=
n
1<=m<=n
1<=m<=n,有:
C
n
m
≡
C
n
m
o
d
p
m
m
o
d
p
∗
C
n
/
p
m
/
p
(
m
o
d
p
)
C_n^m\equiv C_{n\ mod\ p}^{m\ mod\ p}*C_{n/p}^{m/p}(mod\ p)
Cnm≡Cn mod pm mod p∗Cn/pm/p(mod p)
证明:

例题:古代猪文
题
意
:
给
定
整
数
q
,
n
(
1
<
=
q
,
n
<
=
1
e
9
)
题意:给定整数q,n(1<=q,n<=1e9)
题意:给定整数q,n(1<=q,n<=1e9)计算
q
∑
d
∣
n
C
n
d
m
o
d
999911659
q^{\sum_{d|n} C_n^d}mod999911659
q∑d∣nCndmod999911659.
思路:
q
∑
d
∣
n
C
n
d
m
o
d
999911659
=
q^{\sum_{d|n} C_n^d}mod999911659=
q∑d∣nCndmod999911659=
q
∑
d
∣
n
C
n
d
m
o
d
999911658
m
o
d
999911659
q^{\sum_{d|n} C_n^d\ mod\ 999911658}mod999911659
q∑d∣nCnd mod 999911658mod999911659
首先质因数分解9999116658=234679*35617.
然后根据中国剩余定理: 求
x
m
o
d
9999116658
x\ mod\ 9999116658
x mod 9999116658,当然这里x很被计算出来。如果模的是质数就能快得出结果。
M
=
999911658
,
M
i
=
M
P
[
i
]
M=999911658, M_i=\frac{M}{P[i]}
M=999911658,Mi=P[i]M
x
≡
a
1
(
m
o
d
2
)
x\equiv a_1(mod\ 2)
x≡a1(mod 2)
x
≡
a
2
(
m
o
d
3
)
x\equiv a_2(mod\ 3)
x≡a2(mod 3)
x
≡
a
3
(
m
o
d
4679
)
x\equiv a_3(mod\ 4679)
x≡a3(mod 4679)
x
≡
a
4
(
m
o
d
35617
)
x\equiv a_4(mod\ 35617)
x≡a4(mod 35617)
M
i
t
i
≡
1
(
m
o
d
m
i
)
M_it_i\equiv 1(mod\ m_i)
Miti≡1(mod mi)
这里的
t
i
=
M
i
m
i
−
2
t_i=M_i^{m_i-2}
ti=Mimi−2
这里不多赘述啦。 直接
x
=
∑
i
=
1
n
a
i
M
i
t
i
m
o
d
M
x=\sum_{i=1}^n a_iM_it_i\mod M
x=∑i=1naiMitimodM。
然后这里注意一下细节千万别想当然的认为
M
i
t
i
=
M
i
m
i
−
1
M_it_i=M_i^{m_i-1}
Miti=Mimi−1 。
因为这里的模数不是同一个,
M
i
t
i
=
M
i
m
i
−
1
M_it_i=M_i^{m_i-1}
Miti=Mimi−1这样写,我们就默认模数是
m
i
m_i
mi
可是实际的
M
i
t
i
M_it_i
Miti的模数是
M
M
M.所以
t
i
=
M
i
m
i
−
2
t_i=M_i^{m_i-2}
ti=Mimi−2还是老老实实写上。
拆解了四个质数,那就分开来进行计算咯。
ACcode
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define ull unsigned long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
ll gcd(ll a,ll b){ return b? gcd(b,a%b):a;}
const int N=2e5+10;
const ll P=999911659;
ll read(){
ll s = 0, f = 1; char ch = getchar();
while(!isdigit(ch)){
if(ch == '-') f = -1;
ch = getchar();
}
while(isdigit(ch)) s = (s << 3) + (s << 1) + (ch ^ 48), ch = getchar();
return s * f;
}
using namespace std;
ll qpow(ll a,ll x,ll mod){
ll ans=1;
while(x){
if(x&1){
ans=ans*a%mod;
}
a=a*a%mod;
x>>=1;
}
return ans;
}
ll jie[N];
ll a[4];
ll mo[4]={2,3,4679,35617};
void init(int m){
jie[0]=1;
for(int i=1;i<=m;i++){
jie[i]=jie[i-1]*i%m;
}
return ;
}
ll C(ll n,ll m,ll mod){
if(n<m) return 0; // 注意一下这里。小心一点。lucas(8,2,7)=0;
return (jie[n]*qpow(jie[m],mod-2,mod))%mod * qpow(jie[n-m],mod-2,mod)%mod;
}
ll lucas(ll n,ll m,ll mod){
if(n<mod and m<mod){
return C(n,m,mod);
}
return C(n%mod,m%mod,mod)*lucas(n/mod,m/mod,mod)%mod;
}
ll M=P-1;
void solve(){
ll q,n;
n=read();
q=read();
if(q%P==0){
printf("0\n");
return ;
}
for(int i=0;i<4;i++){
init(mo[i]);
ll ans=0;
// cout<<"i:"<<i+1<<endl;
for(int j=1;j*j<=n;j++){
//n的约数j,n/j
if(n%j==0){
// cout<<j<<" "<<lucas(n,j,mo[i])<<endl;
ans=(ans+lucas(n,j,mo[i]))%mo[i];
if(n/j!=j){
// cout<<n/j<<" "<<lucas(n,n/j,mo[i])<<endl;
ans=(ans+lucas(n,n/j,mo[i]))%mo[i];
}
}
}
// cout<<"ans:"<<ans<<endl;
a[i]=ans; //存放在不同模数下的结果。
}
ll sum=0;
// 中国剩余定理
for(int i=0;i<4;i++){
ll Mi=M/mo[i];
// 注意模数 mo[i] 和M。
ll t=Mi*qpow(Mi,mo[i]-2,mo[i])%M;
// cout<<t<<endl;
// cout<<qpow(Mi,mo[i]-1,mo[i])<<endl;
sum= (sum+a[i]*t)%M;
//Mi%M*t%M
}
// cout<<sum<<endl;
printf("%lld\n",qpow(q,sum,P));
return ;
}
int main (){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
solve();
getchar();
getchar();
return 0;
}
Catalan数列
给
定
n
个
0
和
n
个
1
,
排
成
长
度
为
2
n
的
序
列
给定n个0和n个1,排成长度为2n的序列
给定n个0和n个1,排成长度为2n的序列
满足序列任意前缀0的个数都不少于1的个数的序列的数量为:
C
a
t
n
=
C
2
n
n
n
+
1
Cat_n=\frac{C_{2n}^n}{n+1}
Catn=n+1C2nn
证明:n个0和n个1,排成长度为2n的序列,若S不满足序列任意前缀0的个数都不少于1,则存在一个最小的
位置
2
P
+
1
2P+1
2P+1 ,使得前
2
P
+
1
2P+1
2P+1 有P个0和(P+1)个1.而把
S
[
2
P
+
2
,
2
n
]
S[2P+2,2n]
S[2P+2,2n] 的所有数字去反,得到2n的序列有(n-1)个0
和(n+1)个1.
同理对于(n-1)个0和(n+1)个1任意排成的一个长度的2n序列,必然存在一个位置(
2
P
+
1
2P+1
2P+1 )使得,
P
P
P个0和
P
+
1
P+1
P+1个1,
对后面数字取反,得到的2n序列是n个0和n个1。
在上面中就可以得到了一一对应的关系,
即是
"
S
不
满
足
序
列
任
意
前
缀
0
的
个
数
都
不
少
于
1
"
=
=
"
(
n
−
1
)
个
0
和
(
n
+
1
)
个
1
任
意
排
成
的
一
个
长
度
的
2
n
序
列
个
数
"
"S不满足序列任意前缀0的个数都不少于1" == "(n-1)个0和(n+1)个1任意排成的一个长度的2n序列个数"
"S不满足序列任意前缀0的个数都不少于1"=="(n−1)个0和(n+1)个1任意排成的一个长度的2n序列个数"
而对于(n-1)个0和(n+1)个1的排列个数是
C
2
n
n
−
1
C_{2n}^{n-1}
C2nn−1
所以给定n个0和n个1,排成长度为2n的序列,
满足序列任意前缀0的个数都不少于1的个数的序列的数量是
C
2
n
n
−
C
2
n
n
−
1
=
(
2
n
)
!
n
!
n
!
−
(
2
n
)
!
(
n
−
1
)
!
(
n
+
1
)
!
C_{2n}^{n}-C_{2n}^{n-1}=\frac{(2n)!}{n!n!}-\frac{(2n)!}{(n-1)!(n+1)!}
C2nn−C2nn−1=n!n!(2n)!−(n−1)!(n+1)!(2n)!=
(
2
n
)
!
(
n
+
1
−
n
)
n
!
(
n
+
1
)
!
\frac{(2n)!(n+1-n)}{n!(n+1)!}
n!(n+1)!(2n)!(n+1−n)=
C
2
n
n
n
+
1
\frac{C_{2n}^n}{n+1}
n+1C2nn
该推论的一些性质还有:
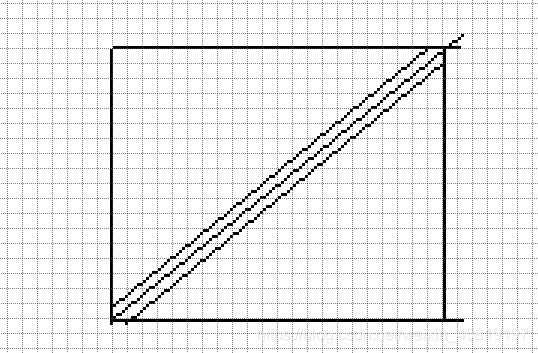
解释一下第四个推论: 要求有些不一样,因为行动的时候不能经过y=x直线,意思就是要么0>1或1<0的有多少次数。
那么我们在对角线画上他旁边的对角线,就可以得知封闭的三角形即是可以有Catalan性质的,
然后0和1是(n-1)个即是(2n-2)序列,两条对角线,所以两种情况, 乘2. 得到 2 C a t n − 1 2Cat_{n-1} 2Catn−1
容斥原理
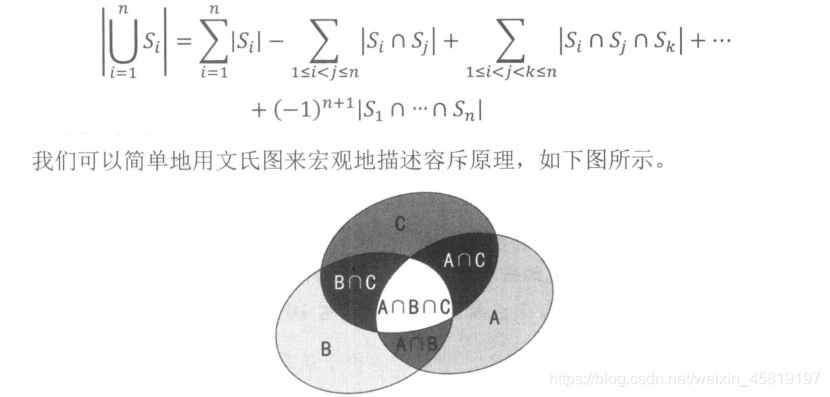
设 S 1 , S 2 , . . . . S n S_1,S_2,....S_n S1,S2,....Sn为有限集合, ∣ S ∣ |S| ∣S∣表示S的大小,则:
∣ U S i ∣ = ∑ i = 1 n ∣ S i ∣ − ∑ 1 < = i < j < = n ∣ S i ∩ S j ∣ + ∑ 1 < = i < j < k < = n ∣ S i ∩ S j ∩ S k ∣ + . . . . + ( − 1 ) n + 1 ∣ S 1 ∩ . . . . ∩ . . . S n ∣ |U_{S_i}|=\sum_{i=1}^n|S_i|-\sum_{1<=i<j<=n}|S_i \cap S_j|+\sum_{1<=i<j<k<=n}|S_i \cap S_j \cap S_k|+....+(-1)^{n+1}|S_1 \cap .... \cap ...S_n| ∣USi∣=∑i=1n∣Si∣−∑1<=i<j<=n∣Si∩Sj∣+∑1<=i<j<k<=n∣Si∩Sj∩Sk∣+....+(−1)n+1∣S1∩....∩...Sn∣
解释一下 ∣ S i ∩ S j ∣ |S_i\cap S_j| ∣Si∩Sj∣,还是挡板的思路,不过一点小区别是, [ n i + n j + 2 , 剩 下 的 元 素 ] [n_i+n_j+2,剩下的元素] [ni+nj+2,剩下的元素].
那么 [ 第 一 个 挡 板 前 的 个 数 − ( n j + 1 ) ] [第一个挡板前的个数-(n_j+1)] [第一个挡板前的个数−(nj+1)]就是 a i a_i ai的个数,然后 第 一 个 和 第 二 个 挡 板 之 间 的 个 数 + n j + 1 第一个和第二个挡板之间的个数+n_j+1 第一个和第二个挡板之间的个数+nj+1就是 a j a_j aj的个数。 后面的 ∣ S i ∩ S j ∩ S k ∣ |S_i\cap S_j \cap S_k| ∣Si∩Sj∩Sk∣等,都是这样得出来的。
莫比乌斯反演 (大部分和容斥原理一起用 )
设正整数N按照算术基本定理分解质因数为
N
=
p
1
c
1
p
2
c
2
.
.
.
.
p
m
c
m
N=p_1^{c_1}p_2^{c_2}....p_m^{c_m}
N=p1c1p2c2....pmcm,定义函数
μ
(
N
)
=
{
0
∃
i
∈
[
1
,
m
]
,
c
i
>
1
1
m
≡
0
(
m
o
d
2
)
,
∀
i
∈
[
1
,
m
]
,
c
i
=
1
−
1
m
≡
1
(
m
o
d
2
)
,
∀
i
∈
[
1
,
m
]
,
c
i
=
1
\mu(N)=\begin{cases} 0 & \exists i\in[1,m],c_i>1 \\ 1 & m\equiv 0(mod\ 2),\forall i \in[1,m],c_i=1 \\ -1 & m\equiv 1(mod\ 2),\forall i\in[1,m],c_i=1\\ \end{cases}
μ(N)=⎩⎪⎨⎪⎧01−1∃i∈[1,m],ci>1m≡0(mod 2),∀i∈[1,m],ci=1m≡1(mod 2),∀i∈[1,m],ci=1
称
μ
\mu
μ为莫比乌斯函数。
通俗地讲,当
N
N
N包含相等的质因子时,
μ
(
N
)
=
0
\mu(N)=0
μ(N)=0.
当
N
N
N的所有的质因子各不相等时.
若N有偶数个质因子,
μ
(
N
)
=
1
\mu(N)=1
μ(N)=1,若
N
N
N有奇数个质因子,
μ
(
N
)
=
−
1
\mu(N)=-1
μ(N)=−1
模板
int V[N],prime[N],miu[N] //最小质因数 素数 μ(N)
void get_miu(int n){
// 用欧拉筛的方式筛
int m=0;
miu[1]=1;
for(int i=2;i<=n;i++){
if(v[i]==0){
v[i]=i,prime[++m]=i;
miu[i]=-1;
}
for(int j=1;j<=m;j++){
if(prime[j]>v[i] || prime[j]*i>n) break;
v[i*prime[j]]=prime[j];
if(miu[i]==0) miu[i*prime[j]]=0;
if(v[i]==prime[j]) miu[i*prime[j]]=0;
else miu[i*prime[j]]=-miu[i];
}
}
rep(i,1,100){
printf("i:%d miu:%d\n",i,miu[i]);
}
return ;
}
例题:Zap
题意:
思路:根据题意要求:可以等价为:多少对二元组 ( x , y ) (x,y) (x,y),满足 x < = a / k , y < = b / k x<=a/k,y<=b/k x<=a/k,y<=b/k,并且x,y互质。 用到容斥原理:(ps:怎么用容斥呢?当发现求解的问题中,转为至少要多少的时候,很得出。就可以往容斥方向思考。)
ACcode
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define ull unsigned long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
ll gcd(ll a,ll b){ return b? gcd(b,a%b):a;}
const int N=2e5+10;
const ll P=1e9+7;
ll read(){
ll s = 0, f = 1; char ch = getchar();
while(!isdigit(ch)){
if(ch == '-') f = -1;
ch = getchar();
}
while(isdigit(ch)) s = (s << 3) + (s << 1) + (ch ^ 48), ch = getchar();
return s * f;
}
using namespace std;
int v[N],prime[N],miu[N];
void get_miu(int n){
int m=0;
miu[1]=1;
for(int i=2;i<=n;i++){
if(v[i]==0){
v[i]=i,prime[++m]=i;
miu[i]=-1;
}
for(int j=1;j<=m;j++){
if(prime[j]>v[i] || prime[j]*i>n) break;
v[i*prime[j]]=prime[j];
if(miu[i]==0) miu[i*prime[j]]=0;
if(v[i]==prime[j]) miu[i*prime[j]]=0;
else miu[i*prime[j]]=-miu[i];
}
}
// 求和
rep(i,1,n){
miu[i]+=miu[i-1];
}
return ;
}
void solve(){
ll x,y,d;
x=read();
y=read();
d=read();
ll a,b;
a=x/d; b=y/d;
ll sum=0;
ll mins=min(a,b);
ll r=0;
for(int i=1;i<=mins;i=r+1){
// a,b区间的左端点为i
// 在两个区间中,得到右端点最小的那个。
r=min(a/(a/i),b/(b/i));
sum+=(miu[r]-miu[i-1])*(a/i)*(b/i);
}
printf("%lld\n",sum);
return ;
}
int main (){
// freopen("in.txt","r",stdin);
// freopen("zap.txt","w",stdout);
get_miu(5e4+10);
int T;
T=read();
while(T--)
solve();
getchar();
getchar();
return 0;
}
概率与数学期望
例题:Rainbow的信号
题意:在 1 N 的 N 个 数 中 , 等 概 率 的 选 取 两 个 数 l 和 r , 如 果 l > r , 则 交 换 l , r 1~N的N个数中,等概率的选取两个数l和r,如果l>r,则交换l,r 1 N的N个数中,等概率的选取两个数l和r,如果l>r,则交换l,r,把 [ l , r ] 的 数 取 出 来 构 成 一 个 P 数 列 [l,r]的数取出来构成一个P数列 [l,r]的数取出来构成一个P数列
思路:数据在 1 e 9 1e9 1e9的范围内,按位来思考,最多32位。对每一位分析结果,和概率期望值。
这里需要明确一点,等概率选取l,r,事件的总和是 N 2 N^2 N2,选取的 l = = r l==r l==r,概率是 1 N 2 \frac{1}{N^2} N21
当l!=r时,这里的l,r并没有要求谁左谁右,概率为 2 N 2 \frac{2}{N^2} N22(ps:假如我等概率选取三个数。 l = r ! = k l=r!=k l=r!=k确定位置的概率为 A 3 3 N 3 \frac{A_3^3}{N^3} N3A33。又或者在前提条件下, l = r ! = k l=r!=k l=r!=k,确定位置的概率是 C 3 2 N 3 ) \frac{C_3^2}{N^3}) N3C32)
(以下都是对位操作来实现,最终结果就是32次位操作之和)操作第k位。 ( k ∈ [ 0 , 31 ] ) (k\in[0,31]) (k∈[0,31])
1.考虑或操作,假如确定了右端点r,想知道那些l可以得到值呢,结果很显然,假设距离r最近的1的位置就是L。 那么 [ 1 , L ] [1,L] [1,L]都可以是l. 还要思考一点r本身就是l。那么前 [ 1 , r − 1 ] [1,r-1] [1,r−1]的概率期望是 P o r + = ( r − 1 ) ∗ 2 N 2 ∗ 2 k P_{or}+=(r-1)*\frac{2}{N^2}*2^k Por+=(r−1)∗N22∗2k
然后是l==r.即是本身 P o r + = 1 N 2 ∗ 2 k P_{or}+=\frac{1}{N^2}*2^k Por+=N21∗2k
2.考虑且操作,同理,固定 r r r,考虑 l l l, [ L , r ] [L,r] [L,r]连续的1是,那么 l l l可以为 l ∈ [ L , r − 1 ] l\in[L,r-1] l∈[L,r−1] 同理 l = r l=r l=r本身.
3.异或操作,固定r,寻找合适的l,满足条件. 如:001000100101考虑最后一个1是r,黑色加粗的即是符合的l.呈现出一个
很显然的规律,这个时候呢,l会是以1为间隔的出现。即是奇数段或者偶数段
Accode
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define ull unsigned long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
ll gcd(ll a,ll b){ return b? gcd(b,a%b):a;}
const int N=2e5+10;
const ll P=1e9+7;
ll read(){
ll s = 0, f = 1; char ch = getchar();
while(!isdigit(ch)){
if(ch == '-') f = -1;
ch = getchar();
}
while(isdigit(ch)) s = (s << 3) + (s << 1) + (ch ^ 48), ch = getchar();
return s * f;
}
using namespace std;
ll a[N];
ld suma,sumo,sumx;
ll c1,c2;
ll last[2];
ld p1,p2;
ll n;
void pre(int k,ll ans){
last[0]=last[1]=0;
c1=c2=0;
int t=1;
ll cnt=0;
for(int i=1;i<=n;i++){
int flag;
if(a[i]&(1<<k)) flag=1;
else flag=0;
// and
if(flag==1){
suma+=ans*p1+cnt*p2*ans;
cnt++;
}else{
cnt=0;
}
// or
if(flag==1){
sumo+=p1*ans+ans*p2*(i-1);
}else{
sumo+=last[1]*p2*ans;
}
// xor
if(flag==1){
sumx+=ans*p1;
if(t==0)
sumx+=c2*p2*ans,c2++;
else sumx+=c1*p2*ans,c1++;
t^=1;
}else{
if(t==0)
sumx+=c1*p2*ans,c2++;
else sumx+=c2*p2*ans,c1++;
}
//位置
if(flag==1)
last[1]=i;
else last[0]=i;
}
// printf("%.3LF %.3LF %.3LF\n",sumx,suma,sumo);
}
void solve(){
n=read();
rep(i,1,n){
a[i]=read();
}
p1=1.0/(n*n);
p2=p1*2;
ll bits=1;
rep(i,0,31){
if(i==0) bits=1;
else bits*=2;
pre(i,bits);
}
printf("%.3LF %.3LF %.3LF\n",sumx,suma,sumo);
}
int main (){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
solve();
getchar();
getchar();
return 0;
}
例题: 绿豆蛙的归宿
题意:
思路:
总结,随便敲敲图的前向性构图方式,图中取反,执行拓扑排序的思想,入队列的点的要求是已经得出了该点u到终点n的期望。
Accode
#include<bits/stdc++.h>
#define ll long long
#define ld long double
#define ull unsigned long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
ll gcd(ll a,ll b){ return b? gcd(b,a%b):a;}
const int N=2e5+10;
const ll P=1e9+7;
ll read(){
ll s = 0, f = 1; char ch = getchar();
while(!isdigit(ch)){
if(ch == '-') f = -1;
ch = getchar();
}
while(isdigit(ch)) s = (s << 3) + (s << 1) + (ch ^ 48), ch = getchar();
return s * f;
}
using namespace std;
ll n,m;
ll ver[N],edge[N],nex[N],head[N];
ll cnt;
void addedge(int x,int y,int value){
ver[++cnt]=y;
edge[cnt]=value;
nex[cnt]=head[x];
head[x]=cnt;
return ;
}
ll in[N],deg[N];
double value[N];
void pre(){
queue<int> q;
q.push(n);
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u];i;i=nex[i]){
int v=ver[i];
// printf("v:%d in:%d\n",v,in[v]);
value[v]+=(value[u]+edge[i])/deg[v];
in[v]--;
if(in[v]==0){
// printf("%d\n",v);
q.push(v);
}
}
}
printf("%.2f\n",value[1]);
return ;
}
void solve(){
//
n=read();
m=read();
ll u,v;
rep(i,1,m){
u=read();
v=read();
addedge(v,u,read());
deg[u]++;
in[u]++;
}
value[n]=0;
pre();
return ;
}
int main (){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
solve();
getchar();
getchar();
return 0;
}
博弈论之SG函数
NIM博弈
用在一推事件是相等的,且博弈的双方都是同等机会公平的选择
结论&定理:NIM博弈先手必胜,当且仅当 A 1 x o r A 2 x o r . . . . . . . x o r A n ≠ 0 A_1\ xor A_2\ xor.......xor\ A_n\neq 0 A1 xorA2 xor.......xor An=0
证明:首先知道a^b=x, 可以得到 x^b=a;
1.当全是0时,0 ^ 0 ^ 0 ^ 0…^ =0
2.如果当前a1^ a2^ a3^ ai…^ an=x; 则可通过一次操作从某堆中取出石子将其转变为 a1^ a2^ a3^ ai’…^an=0;
3.如果当前a1^ a2^ a3^ ai’…^ an=0;则不能通过一次操作再使a1^ a2^ a3^ ai’…^ an=0。 对②证明:由于异或值为x,那么对于a1~an中一定存在ai(二进制)的最高位为1(因为对于异或只有存在1和0才能得1).
那么我们就可以去ai堆,使ai堆只剩下ai^ x(显然:ai>ai^ x 因为ai和x的最高位都为1,异或后为0,比如:a^
b=x,a^ b^x=0,)
现在我们由以上的3个定理,给出石子a1~an,假设此时a1a2a3…an=x(非0);根据定理②我们就可以
操作一步使a1a2a3…an=0;根据定理③对手只能将当前结果变为x(非0);重复执行以上的操作,一定会存在我执行完操作后,每堆石子都为0;对手不能操作,我们胜利。
SG函数
注意:这里的mex(S)是得到不属于集合S的最小非负整数
例题 Cutting game
传送门
题意:

思路:典型的SG算法。必败的初始有(2,2) or (2,3) or (3,2).


ACcode
#include<iostream>
#include<cstring>
#define ll long long
#define ld long double
#define ull unsigned long long
#define rep(i,a,b) for(int i=a;i<=b;i++)
ll gcd(ll a,ll b){ return b? gcd(b,a%b):a;}
const int N=2e5+10;
const ll P=1e9+7;
ll read(){
ll s = 0, f = 1; char ch = getchar();
while(!isdigit(ch)){
if(ch == '-') f = -1;
ch = getchar();
}
while(isdigit(ch)) s = (s << 3) + (s << 1) + (ch ^ 48), ch = getchar();
return s * f;
}
using namespace std;
ll n,m;
int a[205][205];
int dfs(int x,int y){
if(a[x][y]!=-1) return a[x][y];
if((x==2 and (y==2 or y==3)) or (x==3 and y==2)){
a[x][y]=0;
return 0;
}
bool b[250];
memset(b,0,sizeof(b));
for(int i=2;i<=x-i;i++){
b[dfs(i,y)^dfs(x-i,y)]=true;
}
for(int j=2;j<=y-j;j++){
b[dfs(x,j)^dfs(x,y-j)]=true;
}
for(int i=0;;i++){
if(b[i]==0){
a[x][y]=i;
return i;
}
}
}
void solve(){
memset(a,-1,sizeof(a));
// cout<<a[2][3]<<endl;
while(scanf("%d %d",&n,&m)!=EOF){
dfs(n,m);
if(a[n][m]) printf("WIN\n");
else printf("LOSE\n");
}
}
int main (){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
solve();
getchar();
getchar();
return 0;
}





































 1572
1572











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










