一、背景描述
在罗马人占领乔塔帕特后,39 个犹太人与约瑟夫及他的朋友躲到一个洞中,39个犹太人决定宁愿死也不要被敌人抓到,于是决定了一个自杀方式,41个人排成一个圆圈,由第1个人开始报数,每报数到第3人该人就必须自杀,然后再由下一个重新报数,直到所有人都自杀身亡为止。然而约瑟夫和他的朋友并不想遵从。于是,约瑟夫要他的朋友先假装遵从,他将朋友与自己安排在第16个与第31个位置,于是逃过了这场死亡游戏。
二、问题转换
总共有41个人坐成一圈,第一个人的编号为1,第二个人的编号为2,第N个人的编号为N。报数时从编号为1的人开始,编号为1的人报1,编号为2的人报2,依次向后,当出现报数为3的人时,此人退出,然后从退出的下一个人开始重新从1开始报数,以此类推,求出最后退出的人的编号。
三、问题解决
3.1 基础的解决方法
3.1.1 解决思路
此问题可以使用数据结构中的单向循环链表结构来解决。每个结点存储对应的编号,然后从第一个结点开始向后遍历m个结点,然后将第m个结点从此单向循环链表中删除,然后从被删除结点的下一个结点开始继续向后遍历m个结点,以此类推,最后剩余的一个结点的值即为所求的编号。
3.1.2 实现代码
public class BasicSolutions {
//内部结点类
class Node {
//存储编号
private final int number;
//指向下一个结点
private Node next;
public Node(int number, Node node) {
this.number = number;
this.next = node;
}
}
//头节点
private Node head;
//链表长度
private int length;
//类初始化
public BasicSolutions() {
this.head = null;
this.length = 0;
}
/**
* 创建指定长度的链表
*
* @param length 链表长度
*/
public void createLinkList(int length) {
//设置链表的长度
this.length = length;
//初始化头结点
Node node = new Node(1, null);
head = node;
//循环添加结点
for (int i = 2; i <= length; i++) {
node.next = new Node(i, null);
node = node.next;
}
//将末尾结点的next指针指向头结点,实现循环链表
node.next = head;
}
/**
* 按照指定步长删除结点,并返回最后一个结点的值
*
* @param step 步长
* @return 返回删除结点后,链表中剩下的那一个结点的值
*/
public int removeNode(int step) {
Node node = head;
//循环删除结点,直到链表长度为1
while (length > 1) {
//找到需要删除结点的前一个结点
for (int i = 1; i < step - 1; i++) {
node = node.next;
}
//删除节点
node.next = node.next.next;
length--;
//node指向下一次报数为1的结点
node = node.next;
}
return node.number;
}
public static void main(String[] args) {
BasicSolutions list = new BasicSolutions();
list.createLinkList(41);
System.out.println(list.removeNode(3));
}
}3.1.3 算法分析
(1) 时间复杂度分析
设循环链表长度为n,报数步长为m,则创建循环链表需要n,删除结点需要n*m,则时间复杂度为O(n*m+n) ---> O(n*m)
(2) 空间复杂度分析
循环链表的长度为n,则空间复杂度为O(n)
3.2 递归的解决方法
上述基础的模拟循环链表思路比较简单,但是其时间复杂度为O(n*m),当n,m的取值为百万级甚至更大时,其运行时间将会非常大,并消耗大量的资源。而接下来所讲述的递归思路则对该问题做了进一步的优化,所花费的时间与资源会更少。
3.2.1 解决思路
首先讲一下大致的构思。我们将移除一个编号作为一次删除操作,那么对于给定的一个含有n个编号的循环队列总共需要进行 n-1次的删除操作,然后最终会剩下一个编号,而此编号在每一次的删除操作中,该编号在队列中的顺序是不一样的,即队列下标不同,因此只要找到含有n个编号队列的下标与进行一次删除操作后含有n-1个编号队列的下标之间的映射关系,那么就能够进行递归操作,当递归到n为1时,则返回1,递归结束,从而得到最终剩余的那个编号在原本n个编号循环队列中的下标,该下标即为最终所求的编号。
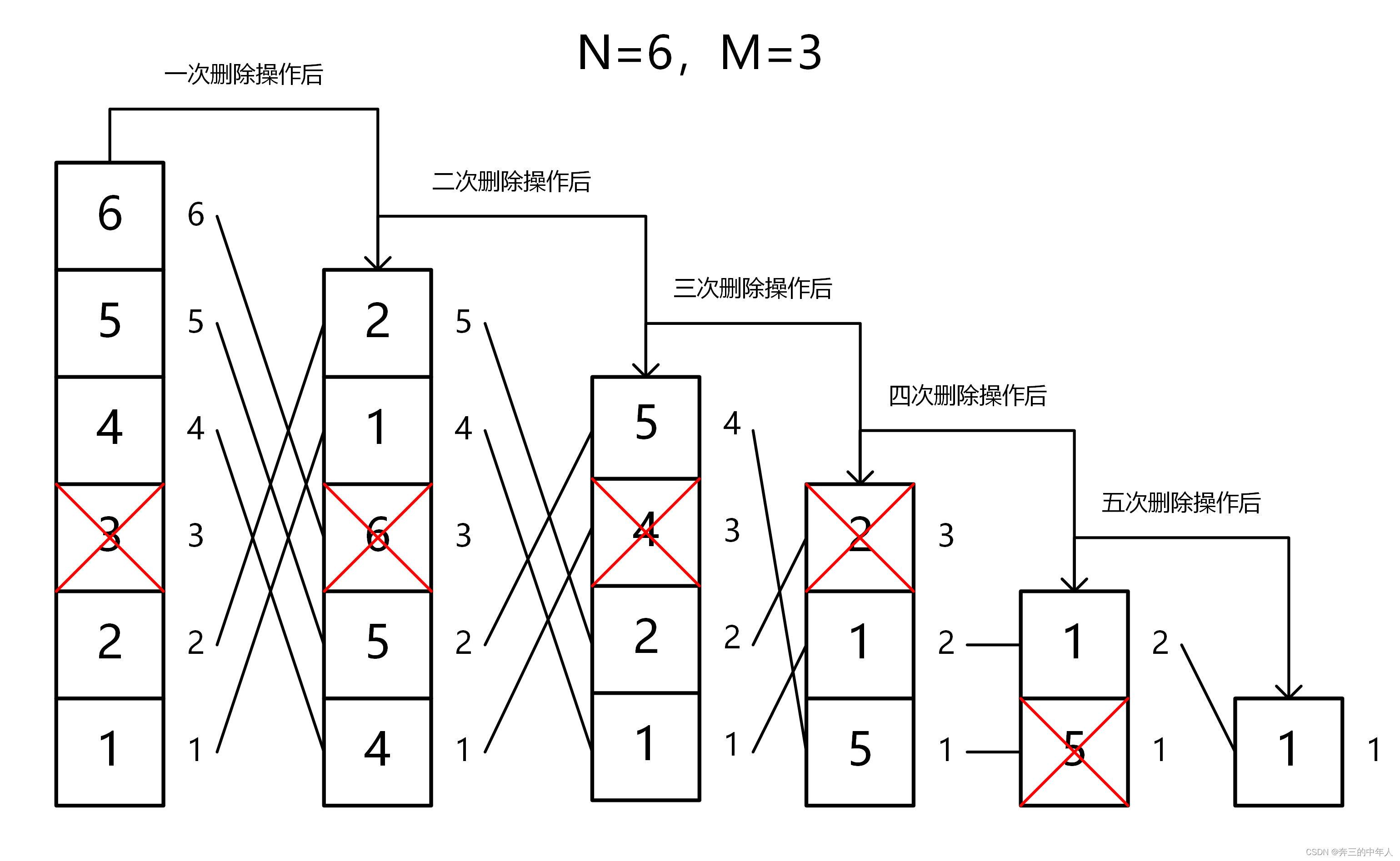
以上图n=6,m=3为例,最终剩余的编号为1,由图可得到编号1的下标变换为1--4--1--2--2--1。
下面进行具体的分析。
设 f(n,m)函数,该函数的返回值为队列中某个未被移除的编号的下标,则可得出固定的 f(1,m)=1。
首先,对于一个含有n个编号,步长为m的队列,可以得出队列的编号如下图所示(队列的编号与下标一致便没有给出)
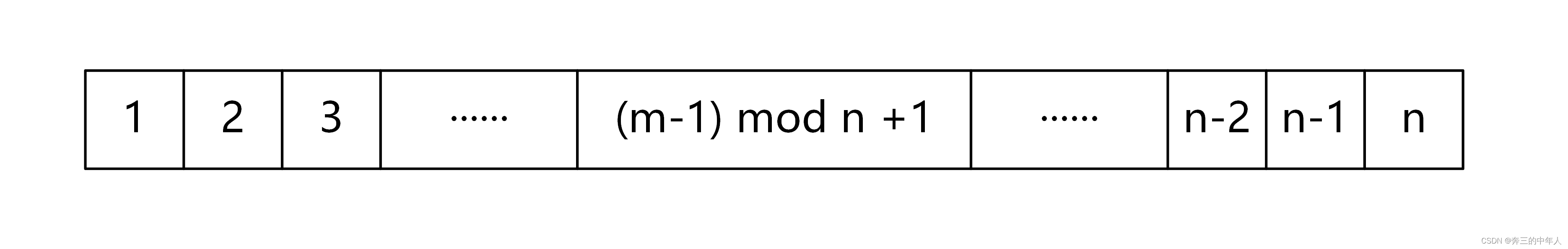
其中(m-1)mod n + 1 处的编号即为我们需要移除的编号,推导过程如下:
当 m <= n 时,移除的编号直接为 m,但是当 m > n 时,便需要对 m进行求余操作,而编号的开始为1,不为0,所以需要先对 m 进行减 1 操作,解决当 m=k*n (k为正整数) 时求余为0的情况,然后再用队列长度求余,再把最后得到的结果加上队列的第一个编号1,最终就能够得到待移除编号为(m-1)mod n + 1,最后通过验证,得出(m-1)mod n + 1同样适用于 m <= n 的情况。
设 M =(m-1)mod n + 1,然后对进行一次删除操作后的队列进行重新排序,可得到下图所示队列 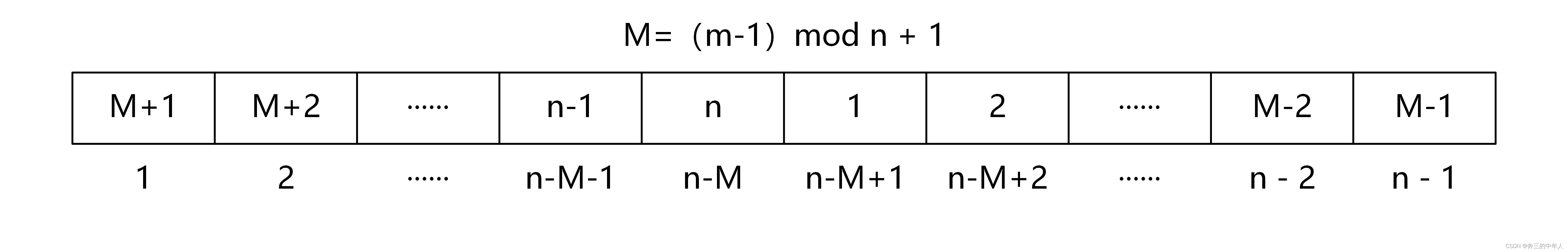
为了便于得出映射关系,将队列按照编号而非下标进行重新排序,可得到下图所示队列

由上图便很容易看出只要下标向左循环平移M个单位便和队列的编号一致。(画×标志表示队列中并不存在此编号,只是为了方便观察下标与编号之间的映射)
因此,设 x 为删除操作后的队列的下标,y 为删除操作后的队列的编号(即原始队列的下标),其中 1 <= x <= n-1,1<= y <= n,然后我们就可以推导出 y =(x + M - 1)mod n + 1 的映射关系式,然后我们将y,x,M用f(n,m),f(n-1,m)和(m-1)mod n + 1替换,就可以得到映射关系f(n, m)=( f(n-1, m) + (m - 1) mod n ) mod n + 1,再将关系式进行化简,便可得到最终的映射关系
f(n, m) = (f(n-1, m) + m - 1) mod n + 1
然后我们来验证下该映射关系式,以上述n=6,m=3为例
最终剩余的编号为1,编号1在每次删除操作中的队列下标变化为1 -- 4 -- 1 -- 2 -- 2 -- 1。然后我们从最后的下标1进行回溯,f(1, 3) = 1,
第一次回溯后下标为 f(2, 3) = (f(1, 3) + 3 - 1) mod 2 + 1 = 2;
第二次回溯后下标为 f(3, 3) = (f(2, 3) + 3 - 1) mod 3 + 1 = 2;
第三次回溯后下标为 f(4, 3) = (f(3, 3) + 3 - 1) mod 4 + 1 = 1;
第四次回溯后下标为 f(5, 3) = (f(4, 3) + 3 - 1) mod 5 + 1 = 4;
第五次回溯后下标为 f(6, 3) = (f(5, 3) + 3 - 1) mod 6 + 1 = 1;
最终的结果 f(6, 3) = 1与我们所期望的结果一致
至此,我们便可以根据此映射关系便可进行递归操作的代码编写了
3.2.2 代码实现
/**
* 递归解决约瑟夫问题
* 映射关系式为 f(n, m) = (f(n-1, m) + m - 1) mod n + 1
*
* @param n 为队列长度
* @param m 为步长
* @return 返回值为队列中某个未被移除的编号的下标
*/
int f(int n, int m) {
return n == 1 ? n : (f(n - 1, m) + m - 1) % n + 1;
}3.2.3 算法分析
(1) 时间复杂度分析
该算法总共进行了 n - 1次递归操作,因此其时间复杂度为O(n)
(2) 空间复杂度分析
一次递归所使用的空间为1,而递归进行了n次,故空间复杂度为O(n)




















 1655
1655











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








