为随机信号x(n)是由白噪激励某一确定系统的响应,只要白噪的参数确定了,研究随机信号就可以转化成研究产生随机信号的系统。
三种参数模型
MA模型(滑动平均模型 Moving average model)
随机信号x(n)由当前的激励w(n)和若干次过去的激励w(n-k)线性组合产生:
x
(
n
)
=
∑
k
=
0
q
b
k
w
(
n
−
k
)
x(n)=\sum_{k=0}^{q}b_{k}w(n-k)
x(n)=k=0∑qbkw(n−k)
该模型的系统函数是:
H
(
z
)
=
X
(
z
)
W
(
z
)
=
∑
k
=
0
q
b
k
z
−
k
H(z)=\frac{X(z)}{W(z)}=\sum_{k=0}^{q}b_{k}z^{-k}
H(z)=W(z)X(z)=k=0∑qbkz−k
q表示系统阶数,系统函数只有零点,没有极点,所以该系统一定是稳定的系统,也称为全零点模型,用 MA( q )来表示。
AR模型(自回归模型 Auto-regression model)
随机信号由本身的若干次过去值x(n-k)和当前的激励值w(n)线性组合产生:
x
(
n
)
=
w
(
n
)
−
∑
k
=
1
p
a
k
x
(
n
−
k
)
x(n)=w(n)-\sum_{k=1}^{p}a_{k}x(n-k)
x(n)=w(n)−k=1∑pakx(n−k)
该模型的系统函数是:
H
(
z
)
=
1
1
+
∑
k
=
1
p
a
k
z
−
k
H(z)=\tfrac{1}{1+\sum_{k=1}^{p}a_{k}z^{-k}}
H(z)=1+∑k=1pakz−k1
p是系统阶数,系统函数中只有极点,无零点,也称为全极点模型,系统由于极点的原因,要考虑到系统的稳定性,因而要注意极点的分布位置,用 AR ( p )来表示。
ARMA模型(自回归滑移平均模型 Auto-regression-Moving average model)
ARMA 是 AR 与 MA 模型的结合:
x
(
n
)
=
∑
k
=
0
q
b
k
w
(
n
−
k
)
−
∑
k
=
1
p
a
k
x
(
n
−
k
)
x(n)=\sum_{k=0}^{q}b_{k}w(n-k)-\sum_{k=1}^{p}a_{k}x(n-k)
x(n)=k=0∑qbkw(n−k)−k=1∑pakx(n−k)
该模型的系统函数是:
H
(
z
)
=
∑
k
=
0
q
b
k
z
−
k
1
+
∑
k
=
1
p
a
k
z
−
k
H(z)=\tfrac{\sum_{k=0}^{q}b_{k}z^{-k}}{1+\sum_{k=1}^{p}a_{k}z^{-k}}
H(z)=1+∑k=1pakz−k∑k=0qbkz−k
它既有零点又有极点,所以也称极零点模型,要考虑极零点的分布位置,保证系统的稳定,用 ARMR( p ,q )表示。
AR 模型参数的估计
AR模型参数和自相关函数的关系
例7.2 已知自回归信号模型 AR(3)为:
x ( n ) = 14 24 x ( n − 1 ) + 9 24 x ( n − 2 ) − 1 24 x ( n − 3 ) + w ( n ) x(n)=\frac{14}{24}x(n-1)+\frac{9}{24}x(n-2)-\frac{1}{24}x(n-3)+w(n) x(n)=2414x(n−1)+249x(n−2)−241x(n−3)+w(n)
式中w(n)是具有方差 σ w 2 = 1 \sigma _{w}^{2}=1 σw2=1的平稳白噪声,求
a. 自相关序列 R x x ( m ) R_{xx}(m) Rxx(m), m=0,1,2,3,4,5。
b. 用 a 求出的自相关序列来估计 AR(3)的参数{ a ^ k \hat{a}_k a^k},以及输入白噪声的方差 σ ^ w 2 \hat{\sigma}_{w}^{2} σ^w2大小。
c. 利用给出的 AR 模型,用计算机仿真给出 32 点观测值 x(n)=[0.4282 1.1454
1.5597 1.8994 1.6854 2.3075 2.4679 1.9790 1.6063 1.2804 -0.2083 0.0577 0.0206 0.3572 1.6572 0.7488 1.6666 1.9830 2.6914 1.2521 1.8691 1.6855 0.6242 0.1763 1.3490 0.6955 1.2941 1.0475 0.4319 0.0312 0.5802 -0.6177],用观测值的自相关序
列直接来估计 AR(3)的参数{ a ^ k \hat{a}_k a^k}以及输入白噪声的 σ ^ w 2 \hat{\sigma}_{w}^{2} σ^w2。
解:使用MATLAB验证
a.
a
1
=
−
14
24
a_{1}=-\frac{14}{24}
a1=−2414 ,
a
2
=
−
9
24
a_{2}=-\frac{9}{24}
a2=−249 ,
a
3
=
1
24
a_{3}=\frac{1}{24}
a3=241
[ R ( 0 ) R ( 1 ) R ( 2 ) R ( 3 ) R ( 1 ) R ( 0 ) R ( 1 ) R ( 2 ) R ( 2 ) R ( 1 ) R ( 0 ) R ( 1 ) R ( 3 ) R ( 2 ) R ( 1 ) R ( 0 ) ] [ 1 a 1 a 2 a 3 ] = [ 1 0 0 0 ] \begin{bmatrix} R(0) & R(1) & R(2) & R(3)\\ R(1) & R(0) & R(1) & R(2)\\ R(2) & R(1) & R(0) & R(1)\\ R(3) & R(2) & R(1) & R(0) \end{bmatrix} \begin{bmatrix} 1\\ a_{1}\\ a_{2}\\ a_{3} \end{bmatrix} = \begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix} ⎣⎢⎢⎡R(0)R(1)R(2)R(3)R(1)R(0)R(1)R(2)R(2)R(1)R(0)R(1)R(3)R(2)R(1)R(0)⎦⎥⎥⎤⎣⎢⎢⎡1a1a2a3⎦⎥⎥⎤=⎣⎢⎢⎡1000⎦⎥⎥⎤
整理得:
[ 1 a 1 a 2 a 3 a 1 1 + a 2 a 3 0 a 2 a 1 + a 3 1 0 a 3 a 2 a 1 1 ] [ R ( 0 ) R ( 1 ) R ( 2 ) R ( 3 ) ] = [ 1 0 0 0 ] \begin{bmatrix} 1 & a_{1} & a_{2} & a_{3}\\ a_{1} & 1+a_{2} & a_{3} & 0\\ a_{2} & a_{1}+a_{3} & 1 & 0\\ a_{3} & a_{2} & a_{1} & 1 \end{bmatrix} \begin{bmatrix} R(0)\\ R(1)\\ R(2)\\ R(3) \end{bmatrix} = \begin{bmatrix} 1\\ 0\\ 0\\ 0 \end{bmatrix} ⎣⎢⎢⎡1a1a2a3a11+a2a1+a3a2a2a31a1a3001⎦⎥⎥⎤⎣⎢⎢⎡R(0)R(1)R(2)R(3)⎦⎥⎥⎤=⎣⎢⎢⎡1000⎦⎥⎥⎤
借助MATLAB计算:
a = [-14 / 24, -9 / 24, 1 / 24];
A = [1, a(1), a(2), a(3);...
a(1), 1 + a(2), a(3), 0;...
a(2), a(1)+a(3), 1, 0;...
a(3), a(2), a(1), 1];
b = [1; 0; 0; 0];
Rxx = A \ b
结果:
Rxx =
4.9377
4.3287
4.1964
3.8654
对于R(4)、R(5),根据公式 R x x ( m ) = − ∑ k = 1 p a k R x x ( m − k ) R_{xx}(m)=-\sum_{k=1}^{p}a_{k}R_{xx}(m-k) Rxx(m)=−∑k=1pakRxx(m−k):
for m = 5 : 6
Rxx(m) = 0;
for k = 1 : 3
Rxx(m) = Rxx(m) - a(k) * Rxx(m - k);
end
end
Rxx
结果:

b.
[ R ( 0 ) R ( 1 ) R ( 2 ) R ( 3 ) R ( 1 ) R ( 0 ) R ( 1 ) R ( 2 ) R ( 2 ) R ( 1 ) R ( 0 ) R ( 1 ) R ( 3 ) R ( 2 ) R ( 1 ) R ( 0 ) ] [ 1 a ^ 1 a ^ 2 a ^ 3 ] = [ σ ^ w 2 0 0 0 ] \begin{bmatrix} R(0) & R(1) & R(2) & R(3)\\ R(1) & R(0) & R(1) & R(2)\\ R(2) & R(1) & R(0) & R(1)\\ R(3) & R(2) & R(1) & R(0) \end{bmatrix} \begin{bmatrix} 1\\ \hat{a}_{1}\\ \hat{a}_{2}\\ \hat{a}_{3} \end{bmatrix} = \begin{bmatrix} \hat{\sigma}_{w}^{2}\\ 0\\ 0\\ 0 \end{bmatrix} ⎣⎢⎢⎡R(0)R(1)R(2)R(3)R(1)R(0)R(1)R(2)R(2)R(1)R(0)R(1)R(3)R(2)R(1)R(0)⎦⎥⎥⎤⎣⎢⎢⎡1a^1a^2a^3⎦⎥⎥⎤=⎣⎢⎢⎡σ^w2000⎦⎥⎥⎤
借助MATLAB计算:
注意 R x x ( 0 ) = 4.9377 R_{xx}(0)=4.9377 Rxx(0)=4.9377,在MATLAB中表示为Rxx(1)
R =[ Rxx(1) Rxx(2) Rxx(3) Rxx(4);...
Rxx(2) Rxx(1) Rxx(2) Rxx(3);...
Rxx(3) Rxx(2) Rxx(1) Rxx(2);...
Rxx(4) Rxx(3) Rxx(2) Rxx(1)];
b = [1; 0; 0; 0];
R \ b
结果:

即
σ
w
2
=
1
\sigma _{w}^{2}=1
σw2=1,
a
1
=
−
14
24
a_{1}=-\frac{14}{24}
a1=−2414 ,
a
2
=
−
9
24
a_{2}=-\frac{9}{24}
a2=−249 ,
a
3
=
1
24
a_{3}=\frac{1}{24}
a3=241 ,
可以得到结论:对AR模型参数是无失真的估计,因为已知 AR 模型,我们可以得到完全的输出观测值,因而求得的自相关函数没有失真,当然也就可以不失真的估计。
c.
样本自相关定义 R x x ( m ) = 1 n ∑ i = 1 n x i x i + m R_{xx}(m)=\frac{1}{n}\sum_{i=1}^{n}x_ix_{i+m} Rxx(m)=n1∑i=1nxixi+m
借助MATLAB计算 R x x ( m ) R_{xx}(m) Rxx(m):
clear; clc;
xn = [0.4282 1.1454 1.5597 1.8994 1.6854 2.3075 2.4679 1.9790...
1.6063 1.2804 -0.2083 0.0577 0.0206 0.3572 1.6572 0.7488...
1.6666 1.9830 2.6914 1.2521 1.8691 1.6855 0.6242 0.1763...
1.3490 0.6955 1.2941 1.0475 0.4319 0.0312 0.5802 -0.6177];
Rxx = xcorr(xn) ./ length(xn);
Rxx = Rxx(length(xn) : end)
结果:

将
R
x
x
(
0
)
=
1.9271
R_{xx}(0)=1.9271
Rxx(0)=1.9271,
R
x
x
(
1
)
=
1.6618
R_{xx}(1)=1.6618
Rxx(1)=1.6618,
R
x
x
(
2
)
=
1.5381
R_{xx}(2)=1.5381
Rxx(2)=1.5381,
R
x
x
(
3
)
=
1.3545
R_{xx}(3)=1.3545
Rxx(3)=1.3545,代入计算
[
R
(
0
)
R
(
1
)
R
(
2
)
R
(
3
)
R
(
1
)
R
(
0
)
R
(
1
)
R
(
2
)
R
(
2
)
R
(
1
)
R
(
0
)
R
(
1
)
R
(
3
)
R
(
2
)
R
(
1
)
R
(
0
)
]
[
1
a
^
1
a
^
2
a
^
3
]
=
[
σ
^
w
2
0
0
0
]
\begin{bmatrix} R(0) & R(1) & R(2) & R(3)\\ R(1) & R(0) & R(1) & R(2)\\ R(2) & R(1) & R(0) & R(1)\\ R(3) & R(2) & R(1) & R(0) \end{bmatrix} \begin{bmatrix} 1\\ \hat{a}_{1}\\ \hat{a}_{2}\\ \hat{a}_{3} \end{bmatrix} = \begin{bmatrix} \hat{\sigma}_{w}^{2}\\ 0\\ 0\\ 0 \end{bmatrix}
⎣⎢⎢⎡R(0)R(1)R(2)R(3)R(1)R(0)R(1)R(2)R(2)R(1)R(0)R(1)R(3)R(2)R(1)R(0)⎦⎥⎥⎤⎣⎢⎢⎡1a^1a^2a^3⎦⎥⎥⎤=⎣⎢⎢⎡σ^w2000⎦⎥⎥⎤
借助MATLAB计算:
R =[ Rxx(1) Rxx(2) Rxx(3) Rxx(4);...
Rxx(2) Rxx(1) Rxx(2) Rxx(3);...
Rxx(3) Rxx(2) Rxx(1) Rxx(2);...
Rxx(4) Rxx(3) Rxx(2) Rxx(1)];
b = [1; 0; 0; 0];
R' \ b
结果:
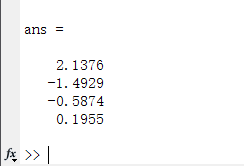

σ
w
2
=
1
2.1376
=
0.4678
\sigma _{w}^{2}= \frac{1}{2.1376} =0.4678
σw2=2.13761=0.4678
a
1
=
−
0.6984
a_{1}=-0.6984
a1=−0.6984 ,
a
2
=
−
0.2748
a_{2}=-0.2748
a2=−0.2748 ,
a
3
=
0.0915
a_{3}=0.0915
a3=0.0915
与真实的AE模型的误差为 e 1 = 0.1151 e_1=0.1151 e1=0.1151, e 2 = 0.1002 e_2=0.1002 e2=0.1002, e 3 = 0.0498 e_3=0.0498 e3=0.0498,原因在于我们只有一部分的观测数据,使得自相关序列值与理想的完全不同。
输入信号的方差误差比较大: e σ = 0.5322 e_\sigma=0.5322 eσ=0.5322,造成的原因比较多,计算机仿真的白噪声由于只有 32 点长,32 点序列的方差不可能刚好等于 1。给出一段观测值求 AR 模型参数这样直接解方程组,当阶数越高时直接解方程组计算就越复杂,因而要用特殊的算法使得计算量减小且精确度高。






















 387
387











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








