275-最长回文字串

问题描述：给你一个字符串 s，找到 s 中最长的回文子串

示例 1：
输入：s = “babad”
输出：“bab”
解释：“aba” 同样是符合题意的答案

示例 2：
输入：s = “cbbd”
输出：“bb”

方法一：动态规划

思路与算法

对于一个子串而言，如果它是回文串，并且长度大于 2，那么将它首尾的两个字母去除之后，它仍然是个回文串，例如对于字符串 "ababa’’，如果我们已经知道 “bab” 是回文串，那么"ababa"一定是回文串，这是因为它的首尾两个字母都是 “a”

根据这样的思路，我们就可以用动态规划的方法解决本题。我们用 P(i,j)P(i,j) 表示字符串 s 的第 i 到 j 个字母组成的串（下文表示成 s[i:j]）是否为回文串：

这里的「其它情况」包含两种可能性：

s[i,j]本身不是一个回文串
i > j，此时 s[i,j] 本身不合法

那么我们就可以写出动态规划的状态转移方程：
P(i,j)=P(i+1,j−1)∧(Si==S j ）

也就是说，只有 s[i+1:j-1]s[i+1:j−1] 是回文串，并且 ss 的第 ii 和 jj 个字母相同时，s[i:j]s[i:j] 才会是回文串。

上文的所有讨论是建立在子串长度大于 2 的前提之上的，我们还需要考虑动态规划中的边界条件，即子串的长度为 1 或 2。对于长度为 1 的子串，它显然是个回文串；对于长度为 2 的子串，只要它的两个字母相同，它就是一个回文串。因此我们就可以写出动态规划的边界条件

在状态转移方程中，我们是从长度较短的字符串向长度较长的字符串进行转移的，因此一定要注意动态规划的循环顺序

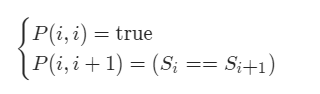
时间复杂度：O(n^2)，其中 n 是字符串的长度
空间复杂度：O(n^2) ，即存储动态规划状态需要的空间，申请的二维数组

当ve[i][j]的长度大于2且s[i]==s[j]时，只需要看s[i+1][j-1]是否为回文串即可，图的填充是往左下角进行填充的

string longestPalindrome(string s) 
{
    int n = s.size();
    if (n <= 1) //如果长度为1，一定是一个回文串,空串也是回文串
    {
        return s;
    }
    int maxLen = 1;//用来保存最大长度
    int begin = 0;//用来保存回文串的起始下标
    // dp[i][j] 表示 s[i..j] 是否是回文串
    vector<vector<int>> dp(n, vector<int>(n));
    // 初始化：所有长度为 1 的子串都是回文串
    for (int i = 0; i < n; i++)
    {
        dp[i][i] = true;
    }
    // 递推开始
    // 先枚举子串长度
    for (int L = 2; L <= n; L++)
    {
        // 枚举左边界，左边界的上限设置可以宽松一些
        for (int i = 0; i < n; i++)
        {
            // 由 L 和 i 可以确定右边界，即 j - i + 1 = L 得
            int j = L + i - 1;
            // 如果右边界越界，就可以退出当前循环
            if (j >= n) break;
            if (s[i] != s[j])//如果左右边界的值不相等，就不是回文串
            {
                dp[i][j] = false;
            }
            else //如果左右边界的值相等并且长度小于等于2，那么一定是，比如aa这种情况
            {
                if (j - i + 1 <= 2)
                {
                    dp[i][j] = true;
                }
                else//只需要看dp[i+1][j-1]是否为回文串
                {
                    dp[i][j] = dp[i + 1][j - 1];
                }
            }
            //只要 dp[i][L] == true 成立，就表示子串 s[i,L] 是回文，此时记录回文长度和起始位置
            if (dp[i][j] && j - i + 1 > maxLen)
            {
                maxLen = j - i + 1;
                begin = i;
            }
        }
    }
    return s.substr(begin, maxLen);
}
int main()
{
    Solution a;
    string b = a.longestPalindrome1("ababcdedf");
    cout << b;
    return 0;
}

方法二：中心扩展法

回文中心的两侧互为镜像。因此，回文可以从他的中心展开，并且只有 2n-1 个这样的中心（一个元素为中心的情况有 n 个，两个元素为中心的情况有 n-1 个）

时间复杂度O(n^2)，空间复杂度O(1)，每个回文中心最多会向外扩展 O(n)O(n) 次

int expendaroundcenter(string s, int left, int right)
//计算以left和right为中心的回文串长度
{
    while (left >= 0 && right < s.size() && s[right] == s[left])
    {
        --left;
        ++right;
    }
    return right - left - 1;
}
string longestPalindrome(string s)
{
    int len = s.size();
    if (len <= 1)//空串也是回文串
        return s;
    int start = 0;//记录回文子串起始位置
    int end = 0;//记录回文子串终止位置
    int maxlen = 0;//记录最大回文子串的长度
    for (int i = 0; i < len; i++)
    {
        int len1 = expendaroundcenter(s, i, i);//一个元素为中心
        int len2 = expendaroundcenter(s, i, i + 1);//两个元素为中心
        maxlen = max(max(len1, len2), maxlen);
        if (maxlen > end - start + 1)
        {
            start = i - (maxlen - 1) / 2;
            end = i + maxlen / 2;
        }
    }
    //该函数的意思是获取从start开始长度为mlen长度的字符串
    return s.substr(start, maxlen);
} 
int main()
{
    string b = longestPalindrome("abcdcba");
    cout << b;
    return 0;
}

方法三：Manacher 算法

时间复杂度：O(n)，空间复杂度：O(n)