填空概念题
- 周期信号频谱的特点 离散性 、收敛性、 谐波性 。
(离手波) - 离散系统要稳定,需要系统函数的所有极点均在 单位圆内 。
(级数收敛) - 频率选择性滤波器的四种基本类型有:( 高通)滤波器、(低通)滤波器、(带通)滤波器和带阻滤波器。
(高通低通、带通带阻) - 当信号是脉冲信号时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿
(信号的能量主要集中在低频分量中,高频细节) - 若f(t)是t的实奇函数,则其F(jw)是w的 虚奇函数
(奇偶虚实性) - 卷积是连续时间系统时域分析的重要手段,请简要叙述两个连续函数进行时域卷积的步骤。
换元,翻转,时移相乘,积分 - 已知信号的拉普拉斯变换为 1 s − α \frac{1}{s-\alpha} s−α1,若实数 α \alpha α 大于零 ,则信号的傅里叶变换不存在.
- 根据Parseval能量守恒定律,计算
∫
−
∞
∞
(
sin
t
t
)
2
d
t
\int_{-\infty}^{\infty}\left(\frac{\sin t}{t}\right)^{2} d t
∫−∞∞(tsint)2dt =π

S a ( t ) < − > π g 2 ( w ) Sa(t)<->\pi g_{2}(w) Sa(t)<−>πg2(w)是一个宽2高 π \pi π的门函数 - 若
f
(
t
)
f(t)
f(t)最高角频率为
w
m
w_{m}
wm,则对
y
(
t
)
=
f
(
t
4
)
f
(
t
2
)
y(t)=f(\frac{t}{4})f(\frac{t}{2})
y(t)=f(4t)f(2t)取样,其频谱不混迭的最大间隔是 .
(时域相乘,频域卷积) ω max = ω m 4 + ω m 2 = 3 4 ω m \omega_{\max }=\frac{\omega_{m}}{4}+\frac{\omega_{m}}{2}=\frac{3}{4} \omega_{m} ωmax=4ωm+2ωm=43ωm
于是 T max = π ω max = 4 π 3 ω m T_{\max }=\frac{\pi}{\omega_{\max }}=\frac{4 \pi}{3 \omega_{m}} Tmax=ωmaxπ=3ωm4π
简单题
- 请给出傅里叶变换、拉普拉斯变换、Z变换的定义式,并简要叙述三者之间的关系?
要点:傅里叶变换是一种特殊的拉式变换,前者要求信号绝对可积。
拉式变换实际上为傅里叶变换的扩展,在收敛域内使得待变换的信号可积。
Z变换是由离散信号的拉式变换而来。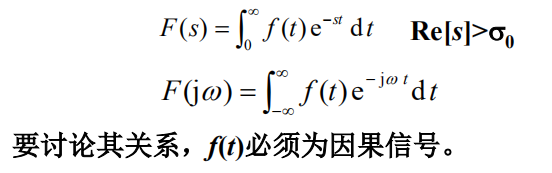
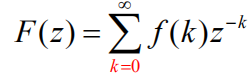
并要简单叙述在Z平面和S平面之间的关系:
在z平面上
θ
\theta
θ每变化
2
π
2\pi
2π,相应于s平面上w变化
2
π
T
\frac{2\pi}{T}
T2π
因此从z平面到s平面的映射是多值的
- 什么是离散信号?
采分关键点:时间域上的定义是离散的。 - 零状态响应的概念是什么?
采分关键点:由输入信号作用下,系统的初始状态为0, - 什么是冲激响应?
采分关键点:由单位冲击信号作为激励,0状态响应 - Z变换存在的充要条件是什么?何为收敛域?
采分关键点:Z变换的级数收敛,使得Z变换存在的z的取值范围 - 如何判断周期性?




- 傅里叶级数





- 抽样定理





























 3359
3359

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








