01背包问题,多重背包问题-分组背包问题-完全背包问题-总结-内含4种经典背包问题

01背包问题：

例题：传送门
01背包问题的特点：背包容量有限，物品只有一个，具有确定的体积和价值，我们的目标就是在不超过背包最大体积的情况下装入价值尽可能大的物品，让我们输出最大总价值

对于背包问题我们可以采用类似的思考方式：

以此为：

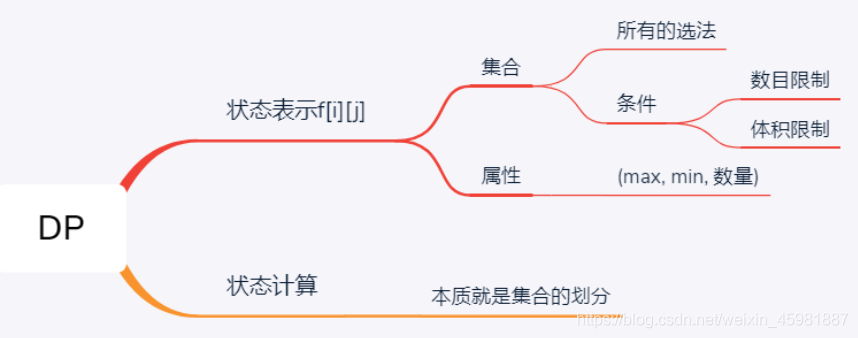
1. 状态表示 考虑所有不同情况的结果存储方式
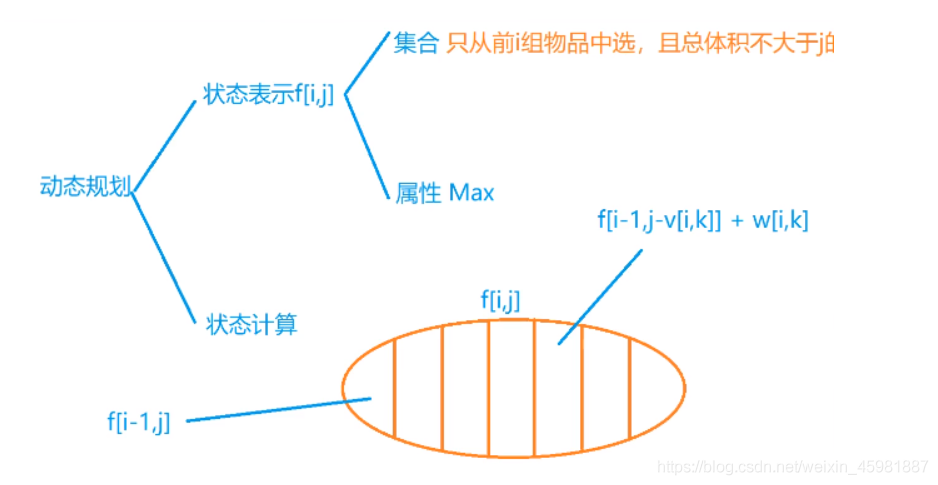
2. 用集合表示背包问题的所有不同选法 f [ i ][ j ] 表示从0 ~ i 这些物品中选，最大背包容量为 j 的最大价值
3. 然后考虑集合选法的条件， 数量 i 小于等于 物品总数 ， 体积 j 小于等于 背包最大体积 V
4. 至于背包问题的属性有已知几个情况：最大值，最小值， 数量
5. 状态计算： 本质就是考虑如何根据上面的条件限制进行合理的集合划分 ， 最终根据集合划分 进行状态转移方程的推导。

01 背包问题实例：

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N,V≤1000
0<vi,wi≤1000
输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

8

我们首先用二维数组的方式来表示背包集合的状态：
对于f [ i ] [ j ] 的值我们可以从第 i 个物品选不选入手，如果第 i 个物品不选那么 f [ i ] [ j ] = f [ i -1 ] [ j ] 即等于上一层的最大价值 即从0~ i-1 个物品中选 且背包容量不超过 j 的最大值 ， 如果在保证不超过背包容量 j 来选第 i 个物品 那么 f [ i ] [ j ] = f [ i -1 ] [ j - v [ i ] +w [ i ]这样我们就得到了容量不超过 j 而且海选则了 第 i 件物品的情况， f [ i ] [ j ] = max （ f [ i -1 ] [ j ]， f [ i -1 ] [ j - v [ i ] + w[ i ]）用循环依次进行这样的操作就得到了所有的状态下的最大价值，最后 f [ n ] [ V ] （n代表 n 个物品 数组的下标从0~ n ，V是背包最大容量） 就是最大价值。

01 背包代码：

#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
const int N=1010;
int n,V;
int v[N];
int w[N];
int dp[N][N];
int maxn;
int main(){
	cin>>n>>V;
	for(int i=1;i<=n;i++){
		scanf("%d%d",&v[i],&w[i]);
	}
	for(int i=1;i<=n;i++){
		for(int vj=1;vj<=V;vj++){
		    if(vj<v[i]) dp[i][vj]=dp[i-1][vj];
			else dp[i][vj]=max(dp[i-1][vj],dp[i-1][vj-v[i]]+w[i]);
		}
	}
	cout<<dp[n][V]<<endl;
	return 0;
}
 

时空复杂度分析和优化：

时间复杂度为O （ n^2 ）主要体现在得到所有状态的过程，这个目前没有更好的优化方式，空间复杂度为 O( n^2 ) 主要体现在我们用一个二维数组存储所有的状态的最大价值，但是通过观察代码我们可以发现每个 dp [ i ] [ j ] 只与 i -1 层的 dp [ i -1] [ j ] 和它之前的 dp [ i- v [ i ] ] [ j ] 有关所以我们没有必要对于i-1 层之前的数值进行存储 ， 我们可以将空间缩小到一维数组， 但是要注意的是如果用一维数组（滚动数组方式）存储第二层的循环 将要逆序循环， 这是因为：如果正序循环，等到循环到 j 时 dp[ j ]用的是i层的数据，这是不符合我们的思路的，当逆序循环是用的就是i-1 层的了。
下面是优化后的代码：

#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
const int N=1010;
int n,V;
int v[N];
int w[N];
int dp[N];
int maxn;
int main(){
    cin>>n>>V;
    for(int i=1;i<=n;i++){
        scanf("%d%d",&v[i],&w[i]);
    }
    for(int i=1;i<=n;i++){
        for(int j=V;j>=v[i];j--){ // 逆序循环 保证dp[j]用到的是上一层的数据
               dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
        }
    }
    cout<<dp[V]<<endl;
    return 0;
}
 

完全背包问题：

例题：传送门
01背包问题的升级版：每种物品有无限个了，而不是01背包问题中的一个，其他说明和01背包相同。

我们依然用闫式dp分析法按照步骤求解，
状态表示：集合 f[ i ][ j ] 表示从第1~i个物品中选 在背包容量不超过j的情况下物品的总最大价值
属性：最大价值
状态划分：可以将f[ i ][ j ]划分为好多种状态，即根据第i个物品选几个。
f[ i ][ j ]=max（f[ i -1 ][ j ]， f[ i -1][ j - v[i]]+w[i]…,f[i-1][j-s*v[i]+w[i]]…）; 1
f [ i ] [ j - v [ i ] ]= max(f[ i-1 ][ j ], f[ i - 1 ] [ j-v[i]] *w[i] …); 2

我们可以用2 式子加上w【i】从第一式的第二项开始替换
从而得到一个比较普遍的式子，
然后我们通过观察对比，这个式子和01背包问题的式子很像，所以可以用滚动数组来优化空间，
由于01 背包每一项用的是上一层（i-1） 的数值，但是完全背包问题由下标可得，是由本层中的前几项获得，所以
状态转移公式为：

//注意v要正序循环
f[j]=max(f[j],f[j-v[i]]+w[i]);

Code:

#include <iostream>
#include <stdio.h>
#include <vector>
#include <cmath>
#include <algorithm> 
#include <map>
#include <string.h>
using namespace std;
const int maxn=1010;
int w[maxn],v[maxn];
int n,m; 
int f[maxn];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		scanf("%d%d",&v[i],&w[i]);
	}
	for(int i=1;i<=n;i++){
		for(int j=v[i];j<=m;j++){
			f[j]=max(f[j],f[j-v[i]]+w[i]);
		}
	}
	cout<<f[m]<<endl;
}

时空复杂度分析：

时间复杂度是O（n^2）空见复杂度为 O（n）n为10^4时都是可以接受的

多重背包问题：

例题：传送门
多重背包问题就是每种物品由多个，不是无限也不是一个，我们可以把它转化为01 背包问题做，思路是：将多个物品拆分成一个一个的，当然这样一定有点麻烦，第二种想法是在数据量小的时候：加一层循环从0循环到s【i】(我们用s【i】来存储第i种物品的个数)；
然后套01背包的代码就可以了

Code：

#include <iostream>
#include <stdio.h>
#include <vector>
#include <cmath>
#include <algorithm> 
#include <map>
#include <string.h>
using namespace std;
const int maxn=110;
int w[maxn],v[maxn],s[maxn];
int n,m; 
int f[maxn];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		scanf("%d%d%d",&v[i],&w[i],&s[i]);
	}
	for(int i=1;i<=n;i++){
		for(int j=m;j>=v[i];j--){
			for(int k=0;k<=s[i] && k*v[i]<=j;k++){
				f[j]=max(f[j],f[j-k*v[i]]+k*w[i]);
			}
		}
	}
	cout<<f[m]<<endl;
}

时空复杂度分析：

时间复杂度O( n ^3) 空间复杂度O( n ) 时间复杂度确实不小，只能承受n不超过100的情况哦

二进制优化降低时间复杂度：

例题：传送门
这道题的数据就加强了，N最坏情况为1000，V是2000，v，w，s都不超过2000，显然用上面的直接暴力做法一定超时，
这里介绍一种二进制的优化方式，降低时间复杂度
对于大数n从1到n进行枚举的这种情况优化明显。
思路：
对于每一个s[ i ] ，从1~ s[ i ] 可以用用几位二进制数进行表示，当表示的最大二进制数小于s[ i ] 时 最后可以用s[ i ]- 最大二进制数表示最后一项数字。
这样我们就把一个大数分成了多组小的数字，用这写小的数字的组合可以组成1~ s[ i ]的任何一个数字。

Code：

#include <iostream>
#include <stdio.h>
#include <vector>
#include <cmath>
#include <algorithm> 
#include <map>
#include <string.h>
using namespace std;
const int maxn=12010;
int w[maxn],v[maxn],s;
int n,V;
int a,b;
int f[maxn];
int main(){
	int cnt=1;
	cin>>n>>V;
	for(int i=1;i<=n;i++){
		scanf("%d%d%d",&a,&b,&s);
		int m=1;
		while(m<=s){
			s-=m;
			v[cnt]=m*a,w[cnt++]=m*b;//分成用每次乘二表示的数打包成一件物品成一项加入数组
			m*=2;
		}
		if(s>0){
			v[cnt]=s*a,w[cnt++]=s*b;//剩下的单成以项，加入数组
		}
	}
	for(int i=1;i<cnt;i++){
		for(int j=V;j>=v[i];j--){
				f[j]=max(f[j],f[j-v[i]]+w[i]);
		}
	}
	cout<<f[V]<<endl;
}

时空复杂度分析：

时间复杂度O（ n^2logn） 在n小于1000时是可以接受的
空间复杂度为O（n）

分组背包问题：

概念：分组背包问题就是，在每一物品组中只选择一个物品
例题：传送门

Code：

#include <cstdio>
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N=110;
const int maxn=24010;
int dp[N];
int n,V; 
int s[N],v[N][N],w[N][N];
int main(){
	cin>>n>>V;
	for(int i=0;i<n;i++){
		cin>>s[i];
		for(int j=0;j<s[i];j++){
			cin>>v[i][j]>>w[i][j];
		}
	}
	for(int i=0;i<n;i++){
		for(int j=V;j>=0;j--){
			for(int k=0;k<s[i];k++){
				if(j>=v[i][k]) dp[j]=max(dp[j],dp[j-v[i][k]]+w[i][k]);
			}
		}
	}
	cout<<dp[V]<<endl;
}