算法与数据结构-动态规划

1 动态规划概述

1.1 从求解斐波那契数列看动态规划法

求解斐波那契数列的递归算法计算过程中存在大量的重复计算

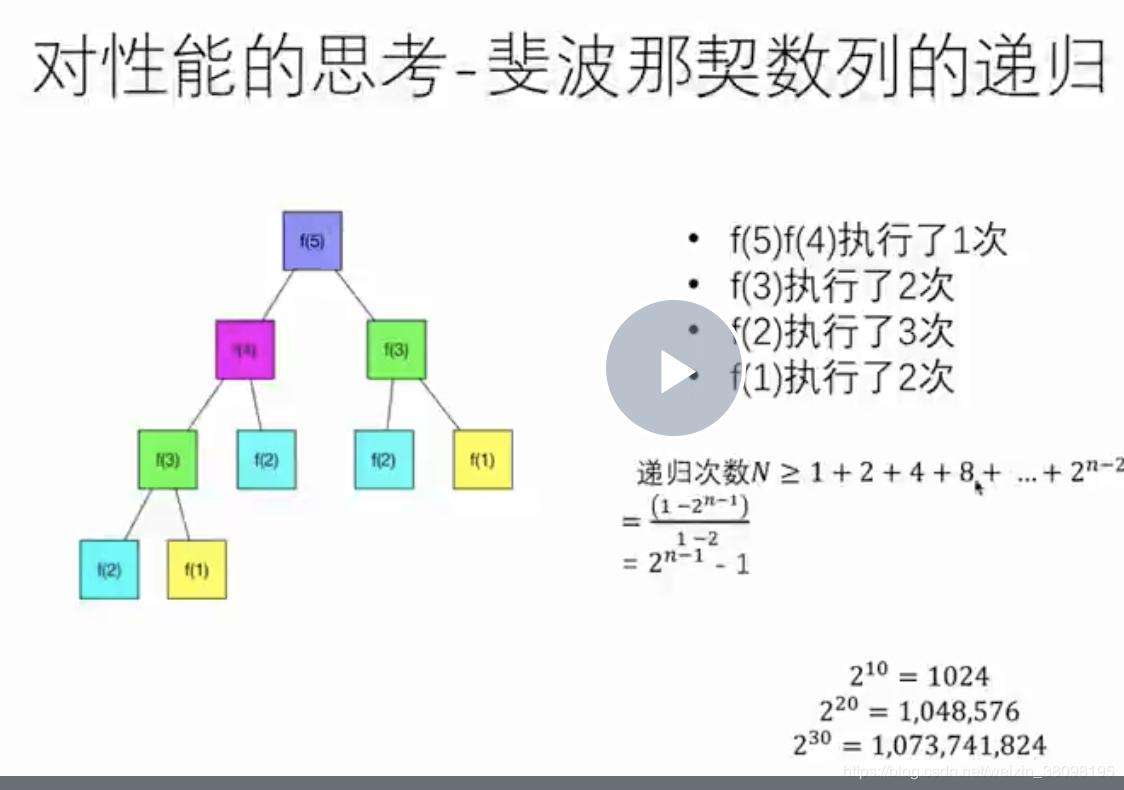
为此避免重复设计，设计一个dp数组，dp[i]存放Fib(i)的值，首先设置dp[1]和dp[2]均为1，再让i从3到n循环以计算dp[3]到dp[n]的值，最后返回dp[n]即Fib1(n)。对应的算法1如下：

int dp[MAX];				//所有元素初始化为0
int count=1;				//累计调用的步骤
int Fib1(int n)			//算法1
{  dp[1]=dp[2]=1;
   printf("(%d)计算出Fib(1)=1\n"，count++);
   printf("(%d)计算出Fib(2)=1\n"，count++);
   for (int i=3;i<=n;i++)
   {  dp[i]=dp[i-1]+dp[i-2];
      printf("(%d)计算出Fib(%d)=%d\n"，count++，i，dp[i]);
   }
   return dp[n];
}

执行Fib1(5)时的输出结果如下：

（1）计算出Fib1(1)=1

（2）计算出Fib1(2)=1

（3）计算出Fib1(3)=2

（4）计算出Fib1(4)=3

（5）计算出Fib1(5)=5

其执行过程改变为自底向上，即先求出子问题解，将计算结果存放在一张表中，而且相同的子问题只计算一次，在后面需要时只有简单查表，以避免大量的重复计算。

上述求斐波那契数列的算法1属于动态规划法，其中数组dp（表）称为动态规划数组。动态规划法也称为记录结果再利用的方法。

1.2 动态规划的原理

动态规划是一种解决多阶段决策问题的优化方法，把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解。

1.3 动态规划的相关概念

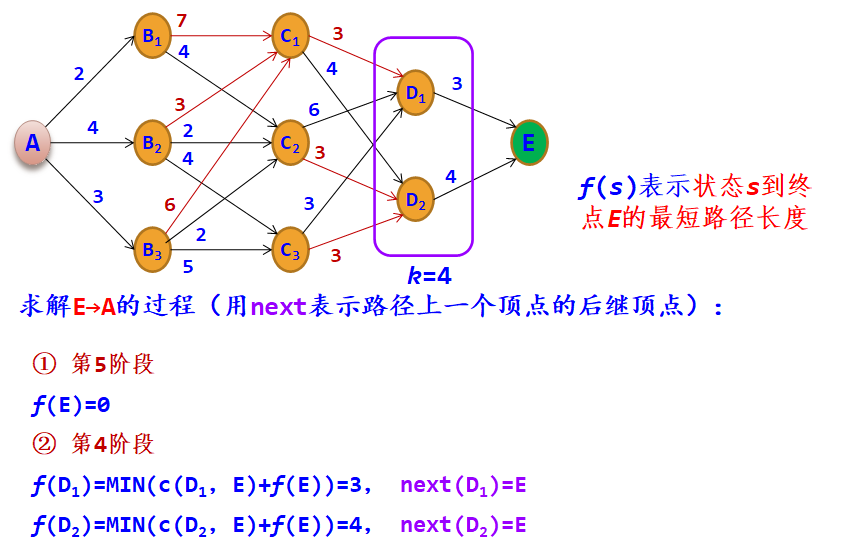
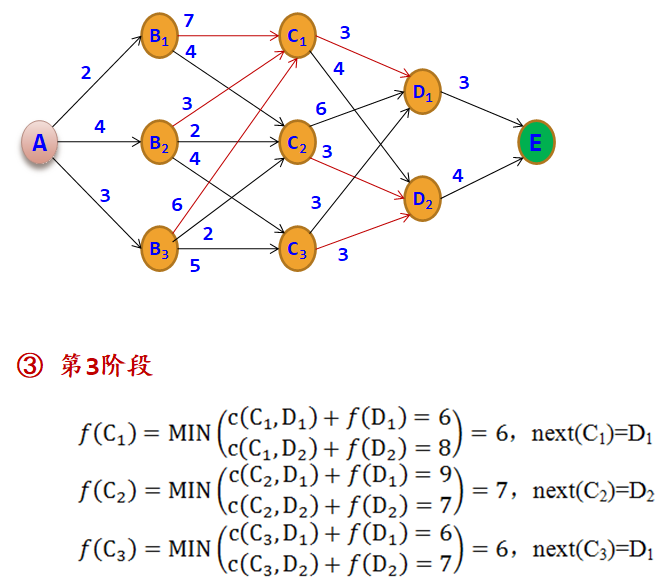
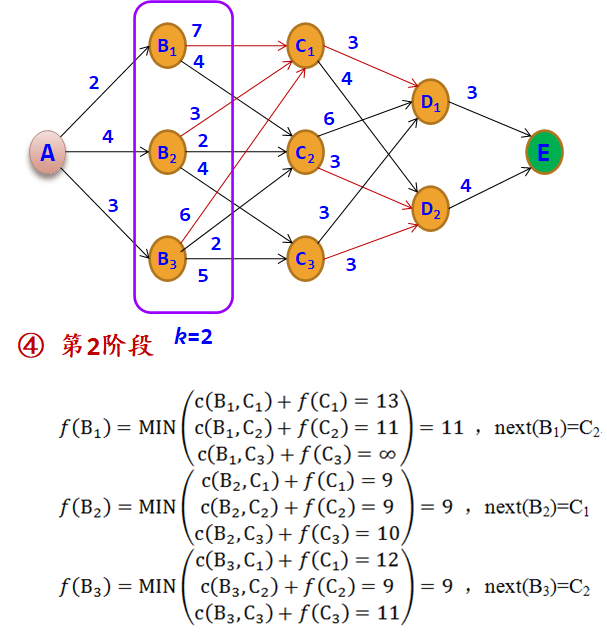
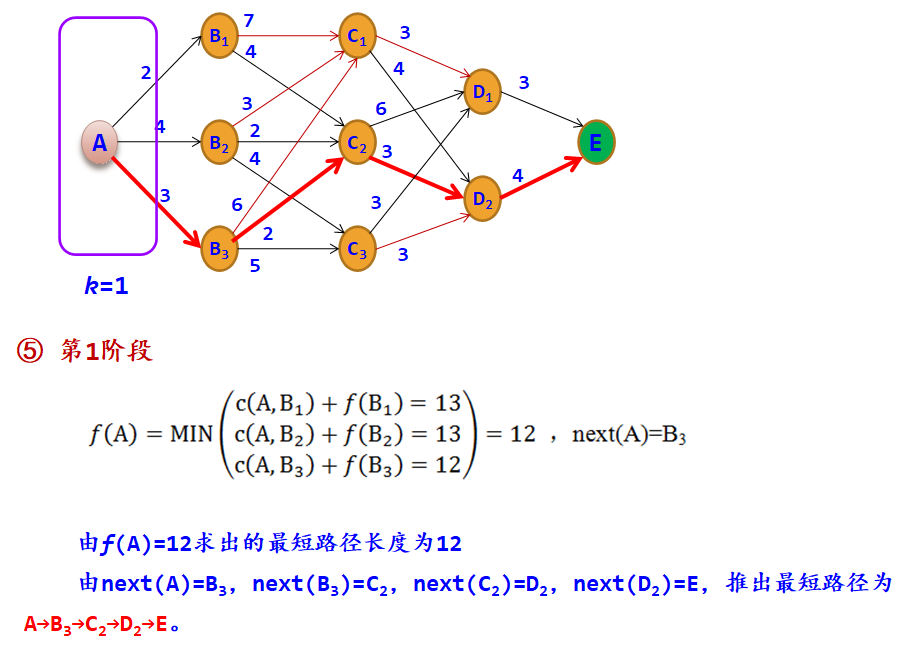
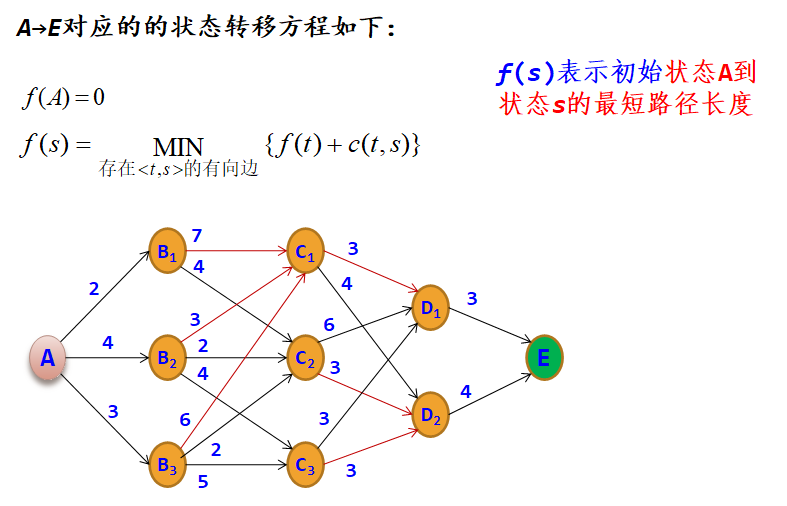
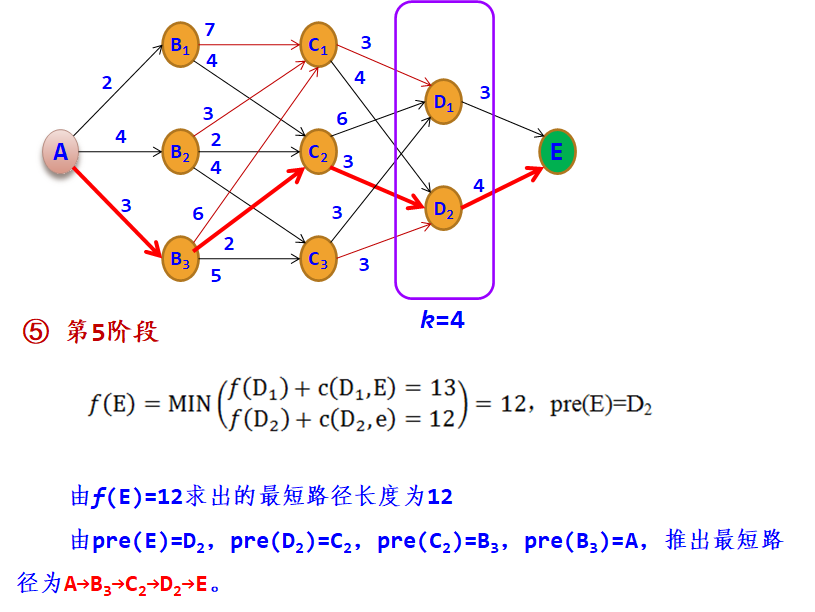
示例：在A处有一水库，现需要从A点铺设一条管道到E点，边上的数字表示与其相连的两个地点之间所需修建的管道长度，用c数组表示，例如c(A，B1)=2。现要找出一条从A到E的修建线路，使得所需修建的管道长度最短。

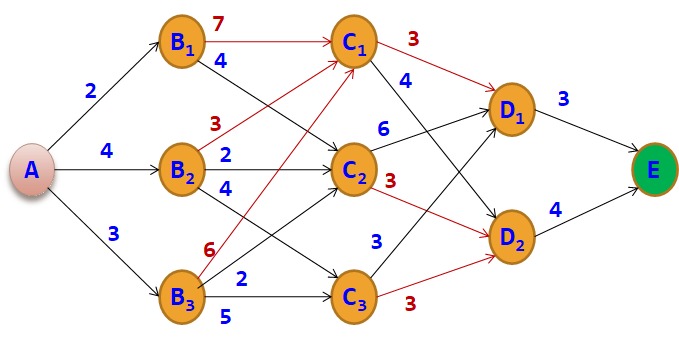
在从A～E的过程中，依据按位置所做的决策的次数及所做决策的先后次序，将问题分为5个阶段，阶段变量用于表示各阶段，这里阶段变量k为1～5，图中第5阶段是虚拟的一个边界阶段。

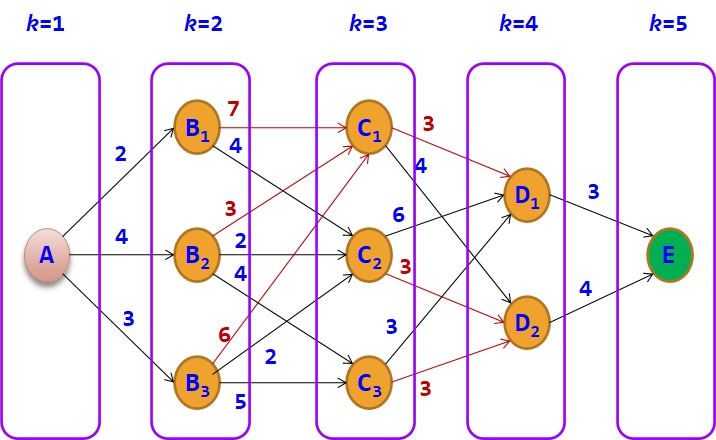
设最优指标函数f(s)表示状态s到终点E的最短路径长度，用k表示阶段，则对应的状态转移方程如下：

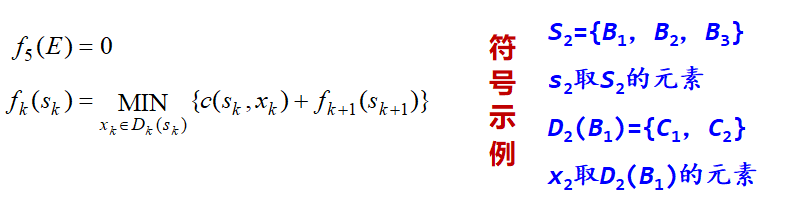
1.4 动态规划问题的解法

逆序解法
顺序解法

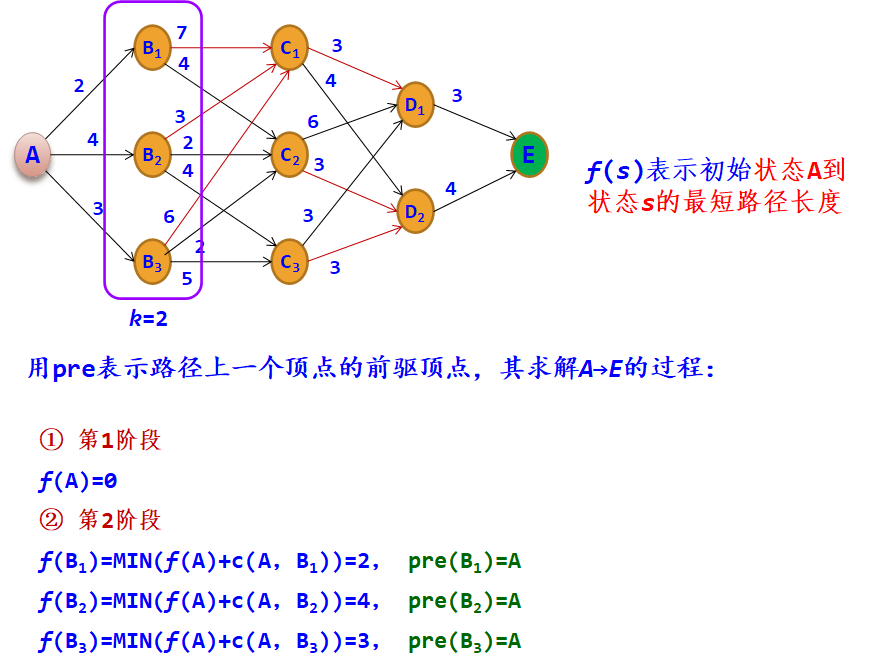
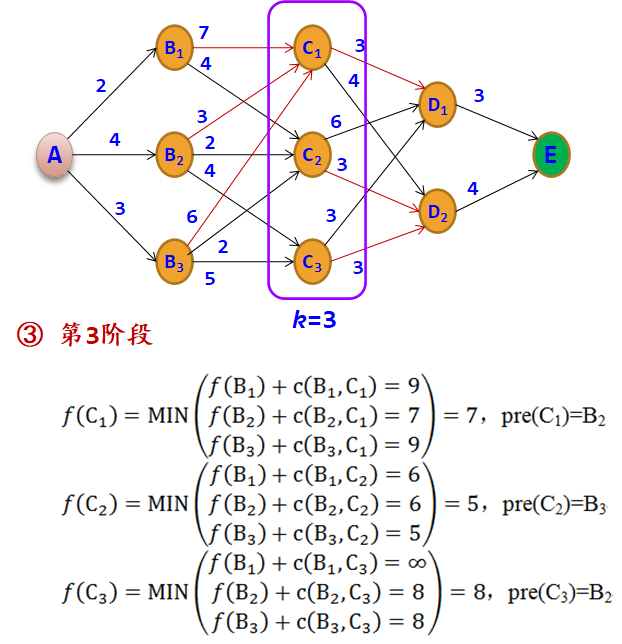
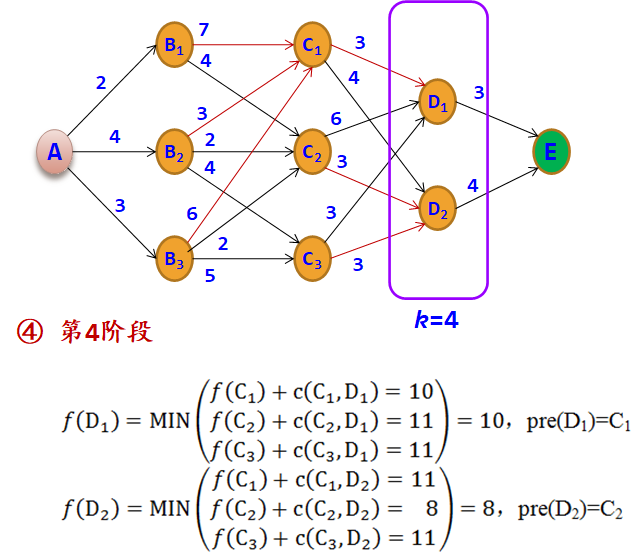
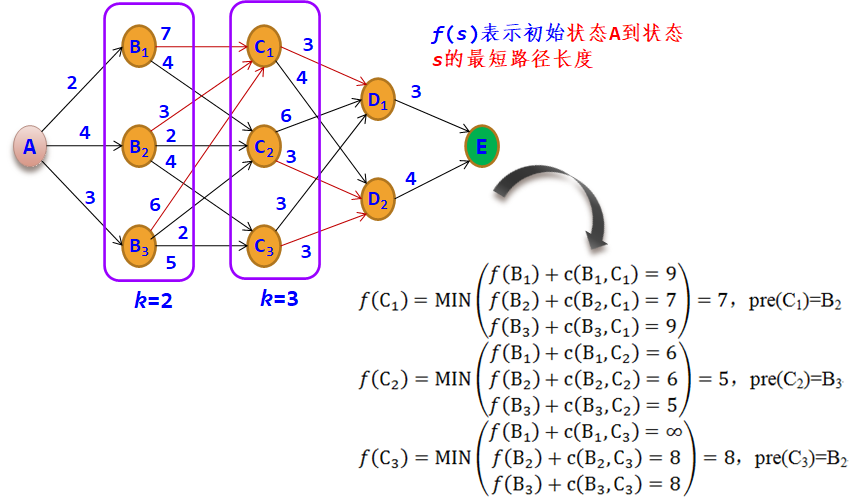
1.4.1 动态规划问题的逆序解法

1.4.2 动态规划问题的顺序解法

1.5 动态规划求解的基本步骤

能采用动态规划求解的问题的一般要具有3个性质：

最优性原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优性原理。

无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。

有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）。

求斐波那契数列

f(1)=1

f(2)=1

f(n)=f(n-1)+f(n-2) n>2

实际应用中简化的步骤：

① 分析最优解的性质，并刻画其结构特征。

② 递归的定义最优解。

③ 以自底向上或自顶向下的记忆化方式计算出最优值。

④ 根据计算最优值时得到的信息，构造问题的最优解。

1.6 动态规划与其他方法的比较

动态规划的基本思想与分治法类似，也是将待求解的问题分解为若干个子问题（阶段），按顺序求解子阶段，前一子问题的解，为后一子问题的求解提供了有用的信息。

在求解任一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其他局部解。依次解决各子问题，最后一个子问题就是初始问题的解。

动态规划方法又和贪心法有些相似，在动态规划中，可将一个问题的解决方案视为一系列决策的结果。

不同的是，在贪心法中，每采用一次贪心准则便做出一个不可回溯的决策，还要考察每个最优决策序列中是否包含一个最优子序列。

2 求解整数拆分问题

【问题描述】求将正整数n无序拆分成最大数为k（称为n的k拆分）的拆分方案个数，要求所有的拆分方案不重复。

【问题求解】设n=5，k=5，对应的拆分方案有：

① 5=5
② 5=4+1
③ 5=3+2
④ 5=3+1+1
⑤ 5=2+2+1
⑥ 5=1+1+1+1
⑦ 5=1+1+1+1+1

为了防止重复计数，让拆分数保持从大到小排序。正整数5的拆分数为7。

采用动态规划求解整数拆分问题。设f(n，k)为n的k拆分的拆分方案个数：

（1）当n=1，k=1时，显然f(n，k)=1。

（2）当n<k时，有f(n，k)=f(n，n)。

（3）当n=k时，其拆分方案有将正整数n无序拆分成最大数为n-1的拆分方案，以及将n拆分成1个n（n=n）的拆分方案，后者仅仅一种，所以有

​ f(n，n)=f(n，n-1)+1。

（4）当n>k时，根据拆分方案中是否包含k，可以分为两种情况：

​ ① 拆分中包含k的情况：即一部分为单个k，另外一部分为{x1，x2，…，xi}，后者的和为n-k，后者中可能再次出现k，因此是（n-k）的k拆分，所以这种拆分方案个数为f(n-k，k)。

​ ② 拆分中不包含k的情况：则拆分中所有拆分数都比k小，即n的（k-1）拆分，拆分方案个数为f(n，k-1)。

​ 因此，f(n，k) = f(n-k，k) + f(n，k-1)

状态转移方程：

f(n，k)= 1 , 当n=1或者k=1

f(n，k)= f(n，n) ,当n<k

​ f(n，k)= f(n，n-1)+1 , 当n=k

​ f(n，k)= f(n-k，k) + f(n，k-1) , 其他情况

显然，求f(n，k)满足动态规划问题的最优性原理、无后效性和有重叠子问题性质。所以特别适合采用动态规划法求解。设置动态规划数组dp，用dp[n][k]存放f(n，k)。

int maxN = 9999;
int[][] dp = new int[maxN][maxN];

void split(int n, int k) {
  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= k; j++) {
      if (i == 1 || j == 1) {
        dp[i][j] = 1;
      } else if (i < j) {
        dp[i][j] = dp[i][i];
      } else if (i == j) {
        dp[i][j] = dp[i][j - 1] + 1;
      } else {
        dp[i][j] = dp[i - j][j] + dp[i][j - 1];
      }
    }
  }
}

split()算法计算dp[5][5]的过程：

（1）dp[2][2]=dp[2][1]+1=1+1=2
（2）dp[2][3]=dp[2][2]=2
（3）dp[3][2]=dp[3][1]+dp[1][2]=1+1=2
（4）dp[5][2]=dp[5][1]+dp[3][2]=1+2=3
（5）dp[5][3]=dp[5][2]+dp[2][3]=3+2=5
（6）dp[5][4]=dp[5][3]+d[1][4]=5+1=6
（7）dp[5][5]=dp[5][4]+1=6+1=7

实际上，该问题本身是递归的，可以直接采用递归算法实现!

int fun(int n, int k) {
  if (n == 1 || k == 1) {
    return 1;
  } else if (n < k) {
    return fun(n, n);
  } else if (n == k) {
    return fun(n, n - 1) + 1;
  } else {
    return fun(n - k, k) + fun(n, k - 1);
  }
}

但由于子问题重叠，存在重复的计算！

可以采用这样的方法避免重复计算：设置数组dp，用dp[n][k]存放f(n，k)，首先初始化dp的所有元素为特殊值0，当dp[n][k]不为0时表示对应的子问题已经求解，直接返回结果。

采用自顶向下（备忘录方法）的动态规划法

int dpf(int n, int k) {
  if (dp[n][k] != 0) {
    return dp[n][k];
  }
  if (n == 1 || k == 1) {
    dp[n][k] = 1;
    return dp[n][k];
  } else if (n < k) {
    dp[n][k] = dpf(n, n);
    return dp[n][k];
  } else if (n == k) {
    dp[n][k] = dpf(n, k - 1) + 1;
    return dp[n][k];
  } else {
    dp[n][k] = dpf(n, k - 1) + dpf(n - k, k);
    return dp[n][k];
  }
}

这种方法是一种递归算法，其执行过程也是自顶向下的，但当某个子问题解求出后，将其结果存放在一张表（dp）中，而且相同的子问题只计算一次，在后面需要时只有简单查表，以避免大量的重复计算。这种方法称之为备忘录方法（memorization method）。
备忘录方法是动态规划方法的变形，与动态规划算法不同的是，备忘录方法的递归方式是自顶向下的，而动态规划算法则是自底向上的。

3 求解最大连续子序列和问题

剑指 Offer 42. 连续子数组的最大和 - 力扣（LeetCode）

【问题求解】对于含有n个整数的序列a，设

​ bj=MAX{ai+ai+1+…+aj} （1≤j≤n）

表示a[1…j]的前j个元素中的最大连续子序列和，则bj-1表示a[1…j-1]的前j-1个元素中的最大连续子序列和。

当bj-1>0时，bj=bj-1+aj，当bj-1≤0时，放弃前面选取的元素，从aj开始重新选起，bj=aj。用一维动态规划数组dp存放b，对应的状态转移方程如下：

dp[0]=0					边界条件
dp[j]=MAX{dp[j-1] +aj，aj} 		1≤j≤n

则序列a的最大连续子序列和等于dp[j]（1≤j≤n）中的最大者。

int dp[MAXN];
void maxSubSum()			//求dp数组
{  dp[0]=0;
   for (int j=1;j<=n;j++)
	dp[j]=max(dp[j-1]+a[j]，a[j]);
}

题解

class Solution {
    public int maxSubArray(int[] nums) {
    int pre=nums[0];
    int max=pre;
    for (int i = 1; i < nums.length; i++) {
      pre=Math.max(pre+nums[i],nums[i]);
      max=Math.max(max,pre);
    }
    return max;
  }
}

4 求解三角形最小路径问题

【问题描述】给定高度为n的一个整数三角形，找出从顶部到底部的最小路径和，只能向下移动相邻的结点。首先输入n，接下来的1～n行，第i行输入i个整数，输出分为2行，第一行为最小路径，第2行为最小路径和。

例如，下图是一个n=4的三角形，输出的路径是2 3 5 3，最小路径和是13。

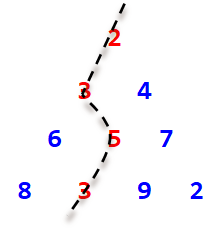
【问题求解】将三角形采用二维数组a存放，前面的三角形对应的二维数组如下：

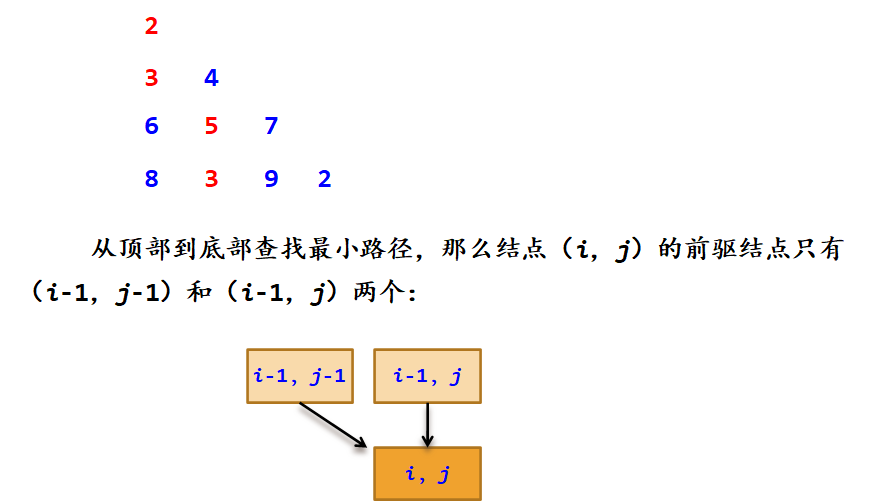
dp[i][j]表示从顶部a[0][0]查找到（i，j）结点时的最小路径和。

一般情况：

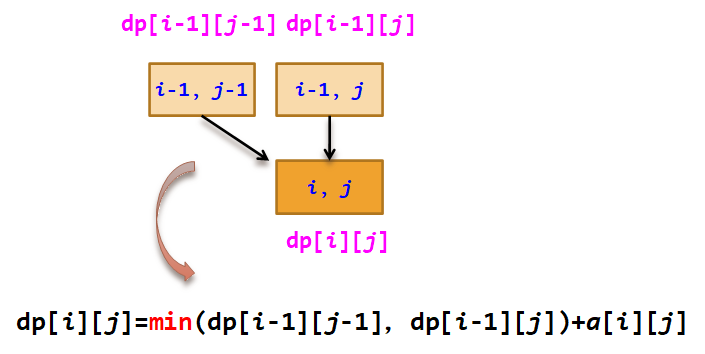
特殊情况:

两个边界，即第1列和对角线，达到它们中结点的路径只有一条而不是常规的两条。

状态转移方程如下：

dp[0][0]=a[0][0]			顶部边界
dp[i][0]=dp[i-1][0]+a[i][0]		考虑第1列的边界，1≤i≤n-1
dp[i][i]=dp[i-1][i-1]+a[i][i]		考虑对角线的边界，1≤i≤n-1
dp[i][j]=min(dp[i-1][j-1]，dp[i-1][j])+a[i][j]  i>1的其他有两条达到
                                                路径的结点

最后求出的最小路径和ans=min(dp[n-1][j])（0≤j<n）。

用pre[i][j]表示查找到（i，j）结点时最小路径上的前驱结点，由于前驱结点只有两个，即（i-1，j-1）和（i-1，j），用pre[i][j]记录前驱结点的列号即可。

在求出ans后，通过pre[n-1][k]反推求出反向路径，最后正向输出该路径。

import java.util.ArrayList;
import java.util.List;

public class TrangleSum {

  //问题表示
  int n = 4;
  int[][] a = new int[n][n];
  //求解结果表示
  int ans = 0;
  int[][] pre = new int[n][n];
  int[][] dp = new int[n][n];

  //求最小和路径ans
  int search() {
    dp[0][0] = a[0][0];
    //考虑第1列的边界
    for (int i = 1; i < n; i++) {
      dp[i][0] = dp[i - 1][0] + a[i][0];
      pre[i][0]=0;
    }
    //考虑对角线的边界
    for (int i = 1; i < n; i++) {
      dp[i][i] = dp[i - 1][i - 1] + a[i][i];
      pre[i][i]=0;
    }
    //考虑其他有两条达到路径的结点
    for (int i = 2; i < n; i++) {
      for (int j = 1; j < i; j++) {
        dp[i][j] = Math.min(dp[i - 1][j], dp[i - 1][j - 1]) + a[i][j];
        pre[i][j] = dp[i - 1][j] > dp[i - 1][j - 1] ? j - 1 : j;
      }
    }
    ans = dp[n - 1][0];
    int k = 0;
    //求出最小ans和对应的列号k
    for (int i = 1; i < n; i++) {
      if (dp[n - 1][i] < ans) {
        k = i;
        ans = dp[n - 1][i];
      }
    }
    return k;  //返回最小和路径最后行的列号k
  }

  //输出最小和路径
  void disppath(int k){
    int i=n-1;
    List<Integer> path=new ArrayList<>();   //存放逆路径向量path
    while (i>=0)  //从（n-1,k）结点反推求出反向路径
    {  path.add(a[i][k]);
      k=pre[i][k];  //最小路径在前一行中的列号
      i--;   //在前一行查找
    }
    for (int j = 0; j < path.size(); j++) {
      System.out.println(path.get(path.size()-j-1));
    }
  }

  public static void main(String[] args) {
    TrangleSum sum = new TrangleSum();
    int[][] ints = new int[][]{{2,0,0,0},{3,4,0,0},{6,5,7,0},{8,3,9,2}};
    sum.a=ints;
    int k = sum.search();
    sum.disppath(k);
  }
}

120. 三角形最小路径和 - 力扣（LeetCode）

class Solution {
  public int minimumTotal(List<List<Integer>> triangle) {
    int[][] dp = new int[triangle.size()][triangle.size()];
    for (int i = 0; i < dp.length; i++) {
      for (int j = 0; j <= i; j++) {
        dp[i][j] = triangle.get(i).get(j);
      }
    }
    for (int i = 1; i < dp.length; i++) {
      dp[i][0] += dp[i - 1][0];
      dp[i][i] += dp[i - 1][i - 1];
    }
    for (int i = 1; i < dp.length; i++) {
      for (int j = 1; j < i; j++) {
        dp[i][j] += Math.min(dp[i - 1][j], dp[i - 1][j - 1]);
      }
    }
    int ans = Integer.MAX_VALUE;
    for (int i = 0; i < dp.length; i++) {
      ans = Math.min(ans, dp[dp.length - 1][i]);
    }
    return ans;
  }
}

5 求解最长公共子序列（LCS）问题

剑指 Offer II 095. 最长公共子序列 - 力扣（LeetCode）

【问题求解】若设A=（a0，a1，…，am-1）（含m个字符），B=（b0，b1，…，bn-1）（含n个字符），设Z=（z0，z1，…，zk-1）（含k个字符）为它们的最长公共子序列。不难证明有以下性质：

定义二维动态规划数组dp，其中dp[i][j]为子序列（a0，a1，…，ai-1）和（b0，b1，…，bj-1）的最长公共子序列的长度。
每考虑字符a[i]或b[j]都为动态规划的一个阶段（共经历约m×n个阶段）。

情况1：a[i-1]=b[j-1]（当前两个字符相同）

dp[i][j]=dp[i-1][j-1]+1

情况2：a[i-1]≠b[j-1]（当前两个字符不同）

dp[i][j]=MAX(dp[i][j-1]，dp[i-1][j])

​ 对应的状态转移方程如下：

dp[i][j]=0				  i=0或j=0―边界条件
dp[i][j]=dp[i-1][j-1]+1		  a[i-1]=b[j-1]
dp[i][j]=MAX(dp[i][j-1]，dp[i-1][j])	  a[i-1]≠b[j-1]

显然，dp[m][n]为最终结果。

那么如何由dp求出LCS呢？ dp => LCS

当dp[i][j] ≠ dp[i][j-1]（左边）并且dp[i][j] ≠ dp[i-1][j]（上方）值时：
     a[i-1]=b[j-1]
将a[i-1]添加到LCS中。

dp[i][j]=dp[i][j-1]：与左边相等 -> j--
dp[i][j]=dp[i-1][j]：与上方相等 -> i--
与左边、上方都不相等：a[i-1]或者b[j-1]属于LCS  -> i--，j--

int[][] dp;

public int longestCommonSubsequence(String text1, String text2) {
  int m = text1.length(), n = text2.length(), i = 1, j = 1;
  dp = new int[m + 1][n + 1];
  for (i = 1; i <= m; i++) {
    //两重for循环处理a、b的所有字符
    for (j = 1; j <= n; j++) {
      //情况(1)
      if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
        dp[i][j] = dp[i - 1][j - 1] + 1;
      } else { //情况(2)
        dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
      }
    }
  }
  //buildSubs
  int k = dp[m][n];
  i = m;
  j = n;
  StringBuilder builder=new StringBuilder();
  while (k > 0) {
    if (dp[i][j] == dp[i - 1][j]) {
      i--;
    } else if (dp[i][j] == dp[i][j - 1]) {
      j--;
    } else   {        //与上方、左边元素值均不相等
      builder.append(text1.charAt(i-1));  
      i--;
      j--;
      k--;
    }
  }
  String lcs = builder.reverse().toString();
  return dp[m][n];
}

【算法分析】 LCSlength算法中使用了两重循环，所以对于长度分别为m和n的序列，求其最长公共子序列的时间复杂度为O(m×n)。空间复杂度为O(m×n)。

6 求解最长递增子序列问题

【问题描述】给定一个无序的整数序列a[0…n-1]，求其中最长递增子序列的长度。

例如，a[]={2，1，5，3，6，4，8，9，7}，n=9，其最长递增子序列为{1，3，4，8，9}，结果为5。

【问题求解】设计动态规划数组为一维数组dp，dp[i]表示a[0…i]中以a[i]结尾的最长递增子序列的长度。对应的状态转移方程如下：

dp[i]=1				0≤i≤n-1
dp[i]=max(dp[i]，dp[j]+1)	若a[i]>a[j]，0≤i≤n-1，0≤j≤i-1

求出dp后，其中最大元素即为所求。

300. 最长递增子序列 - 力扣（LeetCode）

  public int lengthOfLIS(int[] nums) {
    int n = nums.length;
    int[] dp = new int[n];
    for (int i = 0; i < n; i++) {
      dp[i] = 1;
      for (int j = 0; j < i; j++) {
        if (nums[i]>nums[j]){
          dp[i]=Math.max(dp[j]+1,dp[i]);
        }
      }
    }
//    return Arrays.stream(dp).max().getAsInt();
    int ans=dp[0];
    for (int i = 1; i < n; i++) {
      if (dp[i]>ans){
        ans=dp[i];
      }
    }
    return ans;
  }

【算法分析】solve()算法中含两重循环，时间复杂度为O(n2)。

改进 O(nlogn)

动态规划 （包含O (N log N) 解法的状态定义以及解释） - 最长递增子序列 - 力扣（LeetCode）

public int lengthOfLIS(int[] nums) {
  int n = nums.length, end = 0;
  if (n <= 1) {
    return 1;
  }
  // tail 数组的定义：长度为 i + 1 的上升子序列的末尾最小是几
  int[] tail = new int[n];
  tail[0] = nums[0];
  for (int i = 0; i < n; i++) {
    if (nums[i] > tail[end]) {
      end++;
      tail[end] = nums[i];
    } else {
      // 使用二分查找法，在有序数组 tail 中
      // 找到第 1 个大于等于 nums[i] 的元素，尝试让那个元素更小
      int l = 0, r = end;
      while (l < r) {
        int mid = ((r - l) >> 1) + l;
        if (nums[mid] < nums[i]) {
          l = mid + 1;
        } else {
          r = mid;
        }
      }
      tail[l] = nums[i];
    }
  }
  return ++end;
}

7 求解编辑距离问题

72. 编辑距离 - 力扣（LeetCode）

【问题求解】设字符串A、B的长度分别为m、n，分别用字符串a、b存放。

设计一个动态规划二维数组dp，其中dp[i][j]表示将a[0…i-1]（1≤i≤m）与b[0…j-1]（1≤j≤n）的最优编辑距离（即a[0…i-1] 转换为b[0…j-1]的最少操作次数）。

两种特殊情况：

当B串空时，要删除A中全部字符转换为B，即dp[i][0]=i（删除A中i个字符，共i次操作）；
当A串空时，要在A中插入B的全部字符转换为B，即dp[0][j]=j（向A中插入B的j个字符，共j次操作）。

​ 对于非空的情况，当a[i-1]=b[j-1]时，这两个字符不需要任何操作，即dp[i][j]=dp[i-1][j-1]。

​ 当a[i-1]≠b[j-1]时，以下3种操作都可以达到目的：

将a[i-1]替换为b[j-1]，有：dp[i][j]=dp[i-1][j-1]+1（一次替换操作的次数计为1）。
在a[i-1]字符后面插入b[j-1]字符，有：dp[i][j]=dp[i][j-1]+1（一次插入操作的次数计为1）。
删除a[i-1]字符，有：dp[i][j]=dp[i-1][j]+1（一次删除操作的次数计为1）。

此时dp[i][j]取3种操作的最小值。

状态转移方程如下：

dp[i][j]=dp[i-1][j-1]			当a[i-1]=b[j-1]时
dp[i][j]=min(dp[i-1][j-1]+1，dp[i][j-1]+1，dp[i-1][j]+1)	    					
                                        当a[i-1]≠b[j-1]时
                                        
最后得到的dp[m][n]即为所求。

public int minDistance(String word1, String word2) {
  int[][] dp = new int[word1.length()+1][word2.length()+1];
  for (int i = 1; i <= word1.length(); i++) {
    dp[i][0]=i;
  }
  for (int i = 1; i <= word2.length(); i++) {
    dp[0][i]=i;
  }
  for (int i = 1; i <= word1.length(); i++) {
    for (int j = 1; j <= word2.length(); j++) {
      if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
        dp[i][j] = dp[i - 1][j - 1];
      } else {
        dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
      }
    }
  }
  return dp[word1.length()][word2.length()];
}

【算法分析】solve()算法中有两重循环，对应的时间复杂度为O(mn)。

8 求解0/1背包问题

【问题描述】有n个重量分别为{w1，w2，…，wn}的物品，它们的价值分别为{v1，v2，…，vn}，给定一个容量为W的背包。

设计从这些物品中选取一部分物品放入该背包的方案，每个物品要么选中要么不选中，要求选中的物品不仅能够放到背包中，而且重量和为W具有最大的价值。

【问题求解】对于可行的背包装载方案，背包中物品的总重量不能超过背包的容量。

​ 最优方案是指所装入的物品价值最高，即 v1x1+v2x2+…+vn*xn（其中xi取0或1，取1表示选取物品i）取得最大值。

​ 在该问题中需要确定x1、x2、…、xn的值。假设按i=1，2，…，n的次序来确定xi的值，对应n次决策即n个阶段。

设置二维动态规划数组dp，dp[i][r]表示背包剩余容量为r（1≤r≤W），已考虑物品1、2、…、i（1≤i≤n）时背包装入物品的最优价值。显然对应的状态转移方程如下：

dp[i][0]=0（背包不能装入任何物品，总价值为0）	
			边界条件dp[i][0]=0（1≤i≤n）―边界条件
dp[0][r]=0（没有任何物品可装入，总价值为0）	
			边界条件dp[0][r]=0（1≤r≤W）―边界条件
dp[i][r]=dp[i-1][r]	当r<w[i]时，物品i放不下
dp[i][r]= MAX{dp[i-1][r]，dp[i-1][r-w[i]]+v[i]} 	
			否则在不放入和放入物品i之间选最优解

这样， dp[n][W]便是0/1背包问题的最优解。

当dp数组计算出来后，推导出解向量x的过程十分简单，从dp[n][W]开始：

dp[i][r]=dp[i-1][r]	当r<w[i]时，物品i放不下
dp[i][r]= MAX{dp[i-1][r]，dp[i-1][r-w[i]]+v[i]} 	
			否则在不放入和放入物品i之间选最优解

import java.util.Scanner;

public class Main {

  static int N;      //n种物品
  int W;      //限制重量
  int w[];    //存放n个物品重量,不用下标0元素
  int val[];    //存放n个物品价值,不用下标0元素
  int[][] dp;

  int knap() {
    dp = new int[N + 1][W + 1];
    for (int i = 1; i <= N; i++) {
      for (int j = 1; j <= W; j++) {
        if (w[i] > j) {
          dp[i][j] = dp[i - 1][j];
        } else {
          dp[i][j] = Math.max(dp[i - 1][j], dp[i-1][j - w[i]] + val[i]);
        }
      }
    }
    return dp[N][W];
  }

  public static void main(String[] args) {
    Main bag = new Main();
    Scanner scanner = new Scanner(System.in);
    int n = scanner.nextInt();
    int v = scanner.nextInt();
    bag.w = new int[n + 1];
    bag.val = new int[n + 1];
    bag.W = v;
    Main.N = n;
    for (int i = 0; i < n; i++) {
      bag.w[i + 1] = scanner.nextInt();
      bag.val[i + 1] = scanner.nextInt();
    }
    System.out.println(bag.knap());
  }

}

2. 01背包问题 - AcWing题库

9 求解完全背包问题

【问题描述】有n种重量和价值分别为wi、vi（1≤i≤n）的物品，从这些物品中挑选总重量不超过W的物品，求出挑选物品价值总和最大的挑选方案，这里每种物品可以挑选任意多件。

【问题求解】设置动态规划二维数组dp，dp[i][j]表示从前i个物品中选出重量不超过j的物品的最大总价值。

显然有边界条件：dp[i][0]=0（背包不能装入任何物品时，总价值为0），dp[0][j]=0（没有任何物品可装入时，总价值为0）
另外设置二维数组fk，其中fk[i][j]存放dp[i][j]得到最大值时物品i挑选的件数。

状态转移方程：

dp[i][j]=MAX{dp[i-1][j-k*w[i]]+k*v[i]}  当dp[i][j] <
                                 dp[i-1][j-k*w[i]]+k*v[i]（k*w[i]≤j）
fk[i][j]=k;			    	    物品i取k件

​ 这样，dp[n][W]便是背包容量为W、考虑所有n个物品（同一物品允许多次选择）后得到的背包最大总价值，即问题的最优结果。

例如，n=3，W=7，w=(3，4，2)，v=(4，5，3)时，其求解结果如下表所示，表中元素为dp(i，j)[fk(i，j)]，dp(n，W)为最终结果，即最大价值总和为10。

i \ j	0	1	2	3	4	5	6	7
0	0[0]	0[0]	0[0]	0[0]	0[0]	0[0]	0[0]	0[0]
1	0[0]	0[0]	0[0]	4[1]	4[1]	4[1]	8[2]	8[2]
2	0[0]	0[0]	0[0]	4[0]	5[1]	5[1]	8[0]	9[1]
3	0[0]	0[0]	3[1]	4[0]	6[1]	7[1]	9[3]	10[2]

回推过程：
   （1）i=3；dp[3][7]=10，fk[3][7]=2，物品3挑选2件
   （2）i=2；dp[2][W-2×2]=dp[2][3]=4,fk[2][3]=0，物品2挑选0件
   （3）i=1；dp[1][3]=4,fk[1][3]=1，物品1挑选1件。

3. 完全背包问题 - AcWing题库

import java.util.Scanner;

public class Main {

  static int N;      //n种物品
  int W;      //限制重量
  int w[];    //存放n个物品重量,不用下标0元素
  int val[];    //存放n个物品价值,不用下标0元素
  int[][] dp;
  int[][] fk;


  int solve() {
    dp = new int[N + 1][W + 1];
    fk = new int[N + 1][W + 1];
    for (int i = 1; i <= N; i++) {
      for (int j = 0; j <= W; j++) {
        for (int k = 0; k * w[i] <= j; k++) {
          if (dp[i][j] < dp[i - 1][j - k * w[i]] + k * val[i]) {
            dp[i][j] = dp[i - 1][j - k * w[i]] + k * val[i];
            fk[i][j] = k;    //物品i取k件
          }
        }
      }
    }
    return dp[N][W];
  }

  public static void main(String[] args) {
    Main bag = new Main();
    Scanner scanner = new Scanner(System.in);
    int n = scanner.nextInt();
    int v = scanner.nextInt();
    bag.w = new int[n + 1];
    bag.val = new int[n + 1];
    bag.W = v;
    Main.N = n;
    for (int i = 0; i < n; i++) {
      bag.w[i + 1] = scanner.nextInt();
      bag.val[i + 1] = scanner.nextInt();
    }
    System.out.println(bag.solve());
  }

}

【算法分析】solve算法有三重循环，k的循环最坏可能从0到W，所以算法的时间复杂度为O(nW2)。

【算法改进】实际上，上述算法中不必使用k循环，可以修改为在挑选物品i时直接多次重复挑选。

​ 因为计算dp[i][j]中选择k（k≥1）个的情况与在dp[i][j-w[i]]的计算中选择k-1个的情况是相同的，所以dp[i][j]的递推中k≥1部分的计算已经在dp[i][j-w[i]]的计算中完成了。

  int knap() {
    dp = new int[N + 1][W + 1];
    for (int i = 1; i <= N; i++) {
      for (int j = 1; j <= W; j++) {
        if (w[i] > j) {
          dp[i][j] = dp[i - 1][j];
        } else {
          dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - w[i]] + val[i]);
        }
      }
    }
    return dp[N][W];
  }

该算法的时间复杂度为O(nW)。

10 求解资源分配问题

【问题描述】资源分配问题是将数量一定的一种或若干种资源（原材料、资金、设备或劳动力等），合理地分配给若干使用者，使总收益最大。

例如，某公司有3个商店A、B、C，拟将新招聘的5名员工分配给这3个商店，各商店得到新员工后，每年的赢利情况如下表所示，求分配给各商店各多少员工才能使公司的赢利最大？

商店 \ 员工数	0人	1人	2人	3人	4人	5人
A	0	3	7	9	12	13
B	0	5	10	11	11	11
C	0	4	6	11	12	12

【问题求解】采用动态规划求解该问题。设置3个商店A、B、C的编号分别为1～3。

​ 这里总员工数为n=5，商店个数m=3，假设从商店3开始决策起。

​ 设置二维动态规划数组为dp，其中dp[i][s]表示考虑商店i～商店m并分配s个人后的最优赢利。

​ 另外设置二维数组pnum，其中pnum[i][s]表示求出dp[i][s]时对应商店i的分配人数。

对应的状态转移方程如下：

dp[m+1][j]=0			  	边界条件（类似终点的dp值为0）
dp[i][s]=max(v[i][j]+dp[i+1][s-j])	pnum[i][s]=dp[i][s]取最大值的j（0≤j≤n）

显然，dp[1][n]就是最优赢利。

//问题表示
int MAXM = 3, MAXN = 5;
int m = 3, n = 5;        //商店数为m,总人数为n
int[][] v = {{0, 0, 0, 0, 0, 0}, {0, 3, 7, 9, 12, 13},
    {0, 5, 10, 11, 11, 11}, {0, 4, 6, 11, 12, 12}}; //不计v[0]行
//求解结果表示
int[][] dp = new int[MAXM][MAXN];
int[][] pNum = new int[MAXM][MAXN];

//求最优方案dp
void plan() {
  for (int i = m; i >= 1; i--) {
    for (int s = 1; s <= n; s++) {
      int maxf = 0, maxj = 0;
      for (int j = 0; j <= s; j++) {    //找该商店最优情况maxf和分配人数maxj
        if ((v[i][j] + dp[i + 1][s - j]) >= maxf) {
          maxf = v[i][j] + dp[i + 1][s - j];
          maxj = j;
        }
      }
      dp[i][s] = maxf;
      pNum[i][s] = maxj;
    }
  }
}

11 求解会议安排问题

​ 问题描述：陈老师是一个比赛队的主教练。有一天，他想与团队成员开会，应该为这次会议安排教室。教室非常缺乏，所以教室管理员必须接受订单和拒绝订单以优化教室的利用率。如果接受一个订单，该订单的开始时间和结束时间成为一个活动。每个时间段只能安排一个订单（即假设只有一个教室）。请你找出一个最大化的总活动时间的方法。你的任务是这样的：读入订单，计算所有活动（接受的订单）占用时间的最大值。

​ 输入：标准的输入将包含多个测试案例。对于每个测试案例，第一行是一个整数n（n≤10000），接着的n行中每一行包括两个整数p和k（1≤p≤k≤300000），其中p是一个订单开始时间，k是的结束时间。

​ 输出：对于每个测试案例，输出一行包括所有活动占用时间的最大值。

实例：11个订单（已按结束时间的递增排列）

订单i	0	1	2	3	4	5	6	7	8	9	10
开始时间	1	3	0	5	3	5	6	8	8	2	12
结束时间	4	5	6	7	8	9	10	11	12	13	15

【问题求解】由于只有一个教室，两个订单不能相互重叠，两个时间不重叠的订单称为兼容订单。给定若干订单，安排的所有订单一定是兼容订单，拒接不兼容的订单。

​ 用数组A存放所有的订单，A[i].b（0≤i≤n-1）存放订单i的起始时间，A[i].e存放订单i的结束时间，订单i的持续时间A[i].length=A[i].e-A[i].b。

这里采用贪心法+动态规划的思路，先将订单数组A按结束时间递增排序，设计一维动态规划数组dp，dp[i]表示A[0…i]的订单中所有兼容订单的最长时间。对应的状态转移方程如下：

dp[0]=订单0的时间
dp[i]=max{dp[i-1]，dp[j]+A[i].length}    订单j是结束时间早于
					     订单i开始时间的最晚的订单

最后求出的dp[n-1]就是满足要求的结果。

另外为了求出选中的哪些订单，设计一维数组pre，pre[i]表示dp[i]的前驱订单，这里有3种情况：

若A[i]没有前驱订单，pre[i]设置为-1。例如订单0没有前驱订单，置pre[0]=-1。
若不选择订单A[i]，pre[i]设置为-2。例如，i=2时，该方案已经选中了订单1但不选中订单2，则pre[2]=-2。
若选择订单A[i]并且它前面最晚的前驱订单为A[j]，则pre[i]设置为j。例如，该方案已经选中了订单1、3，考虑i=5时，前面最晚的前驱订单订单3，则pre[5]=3。

​ 由于所有订单是按结束时间递增排序的，所以可以采用二分查找方法在A[0…i-1]中查找A[j].e≤A[i].b的最后一个A[j]。

import java.util.Arrays;

public class Conference {

  int n = 11;  //订单个数
  NodeType[] A = {new NodeType(1, 4), new NodeType(3, 5), new NodeType(0, 6),
      new NodeType(5, 7), new NodeType(3, 8), new NodeType(5, 9),
      new NodeType(6, 10), new NodeType(8, 11), new NodeType(8, 12),
      new NodeType(2, 13), new NodeType(12, 15)};
  int[] dp = new int[n + 1];
  int[] pre = new int[n + 1];

  void solve() {
    Arrays.sort(A, (o1, o2) -> {
      return o1.e - o2.e;
    });
    dp[0] = A[0].length;
    pre[0] = -1;
    for (int i = 1; i < n; i++) {
      int low = 0, high = i - 1;
      //在A[0..i-1]中查找结束时间早于A[i].b的最晚订单A[low-1]
      while (low <= high) {
        int mid = (low + high) / 2;
        if (A[mid].e < A[i].b) {
          low = mid + 1;
        } else {
          high = mid - 1;
        }
      }
      if (low == 0) {
        if (dp[i - 1] >= A[i].length) {
          dp[i] = dp[i - 1];
          pre[i] = -2;      //不选中订单i
        } else {
          dp[i] = A[i].length;
          pre[i] = -1;      //没有前驱订单
        }
      } else {
        //A[i]前面最晚有兼容订单A[low-1]
        if (dp[i - 1] >= dp[low - 1] + A[i].length) {
          dp[i] = dp[i - 1];
          pre[i] = -2;      //不选择订单i
        } else {
          dp[i] = dp[low - 1] + A[i].length;
          pre[i] = low - 1;    //选中订单i
        }
      }
    }
  }
}

class NodeType {

  int b;      //开始时间
  int e;      //结束时间
  int length;      //订单的执行时间

  public NodeType(int b, int e) {
    this.b = b;
    this.e = e;
    this.length = e - b;
  }
}

订单i	0	1	2	3	4	5	6	7	8	9	10
开始时间	1	3	0	5	3	5	6	8	8	2	12
结束时间	4	5	6	7	8	9	10	11	12	13	15

求解结果

​ 选择的订单:2[0,6] 6[6,10] 10[12,15]

​ 兼容订单的总时间:13

【算法分析】在solve()算法中，一共循环n次，二分查找的时间为O(log2n)，所以算法的时间复杂度为O(nlog2n)。

12 滚动数组

12.1 什么是滚动数组

​ 在动态规划算法中，常用动态规划数组存放子问题的解，由于一般是存放连续的解，有时可以对数组的下标进行特殊处理，使每一次操作仅保留若干有用信息，新的元素不断循环刷新，看上去数组的空间被滚动地利用，这样的数组称为滚动数组（Scroll array）。

​ 采用滚动数组的主要目的是压缩存储空间的作用。

int dp[MAX];				//所有元素初始化为0
int count=1;				//累计调用的步骤
int Fib1(int n)			//算法1
{  dp[1]=dp[2]=1;
   printf("(%d)计算出Fib(1)=1\n"，count++);
   printf("(%d)计算出Fib(2)=1\n"，count++);
   for (int i=3;i<=n;i++)
   {  dp[i]=dp[i-1]+dp[i-2];
      printf("(%d)计算出Fib(%d)=%d\n"，count++，i，dp[i]);
   }
   return dp[n];
}

//只需要使用dp[0]、dp[1]和dp[2] 3个元素空间
int Fib2(int n)		//Fib算法2
{  int dp[3];
   dp[1]=1; dp[2]=1;
   for (int i=3;i<=n;i++)
      dp[i % 3]=dp[(i-2)%3]+dp[(i-1)%3];
   return dp[n%3];
}

12.2 滚动数组求解0/1背包问题

  int knap() {
    dp = new int[2][W+1];
    int c=0;
    for (int i = 1; i <= N; i++) {
      c=1-c;
      for (int j = 1; j <= W; j++) {
        if (w[i] > j) {
          dp[c][j] = dp[1-c][j];
        } else {
          dp[c][j] = Math.max(dp[1-c][j], dp[1-c][j - w[i]] + val[i]);
        }
      }
    }
    return dp[c][W];
  }

【例】一个楼梯有n个台阶，上楼可以一步上1个台阶，也可以一步上2个台阶，求上楼梯共有多少种不同的走法。

70. 爬楼梯 - 力扣（LeetCode）

    public int climbStairs(int n) {
        int[] dp=new int[2];
        dp[0]=dp[1]=1;
        for(int i=2;i<=n;i++){
            dp[i%2]=dp[(i-1)%2]+dp[(i-2)%2];
        }
        return dp[n%2];
    }

思考题：CSP认证题

试题名称：任务调度

时间限制：1.0s

内存限制：256.0MB

问题描述：有若干个任务需要在一台机器上运行。它们之间没有依赖关系，因此 可以被按照任意顺序执行。

该机器有两个CPU和一个GPU。对于每个任务，你可以为它分配不同的硬件资源：

\1. 在单个CPU上运行。

\2. 在两个CPU上同时运行。

\3. 在单个CPU和GPU上同时运行。

\4. 在两个CPU和GPU上同时运行。

一个任务开始执行以后，将会独占它所用到的所有硬件资源，不得中断，直到执行结束为止。第i个任务用单个CPU，两个CPU，单个CPU加GPU，两个CPU加GPU运行所消耗的时间分别为ai，bi，ci 和 di。

现在需要你计算出至少需要花多少时间可以把所有给定的任务完成。

输入格式：输入的第一行只有一个正整数 n(1 ≤ n ≤ 40)， 是总共需要执行的任 务个数。接下来的 n 行每行有四个正整数ai，bi，ci，di(ai，bi，ci，di 均不超过10)，以空格隔开。
输出格式：输出只有一个整数，即完成给定的所有任务所需的最少时间。
样例输入：
3
4 4 2 2
7 4 7 4
3 3 3 3
样例输出
7
样例说明：有很多种调度方案可以在7个时间单位里完成给定的三个任务，以下是其中的一种方案：同时运行第一个任务（单CPU加上GPU）和第三个任务（单CPU），它们分别在时刻2和时刻3完成。在时刻3开始双CPU运行任务2，在时刻7完成。

3201. 任务调度 - AcWing题库