操作系统：内存可变分区分配与回收以及其相关算法的介绍

一、基本介绍：

基本思想：

系统并不预先划分内存区间，而是在作业装入时根据作业的实际需要动态地划分内存空间。若无空闲的存储空间或无足够大的空闲存储空间供分配时，则令该作业等待

分配中的数据结构：

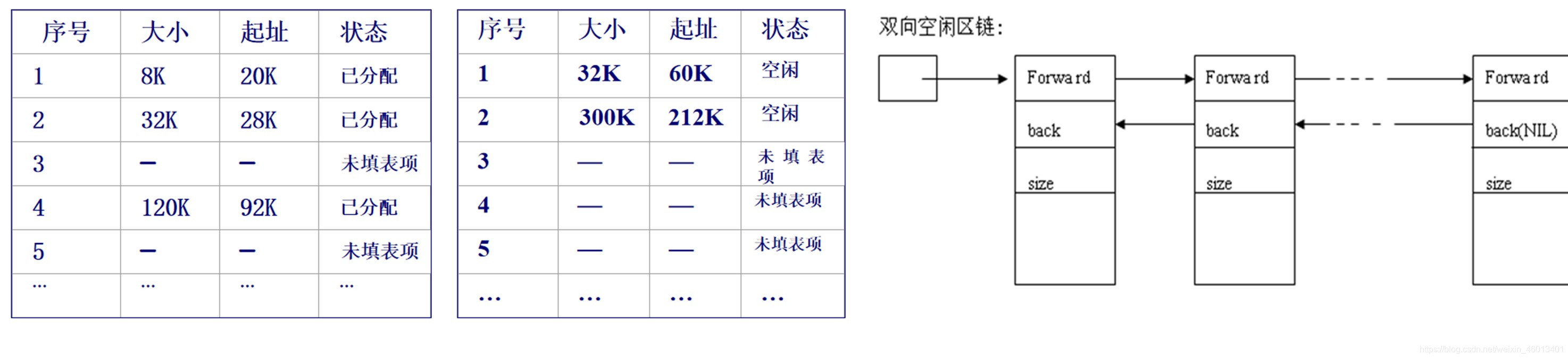
常用的数据结构有已分分区表和空闲分区表或空闲分区链表。

• 已分分区表：记录当前已经分配给用户作业的内存分区，包括分区序号、开始地址、分区大小等信息。（记录已经使用了的空间）
• 空闲分区表：记录了当前内存中空闲分区的情况，包括分区序号、开始地址、分区大小。（记录未分配使用的空间）
• 空闲分区链表：将空闲分区组织成为链表的形式。

已分分区表、空闲分区表和空闲分区链表

可变分区示例：

---

 

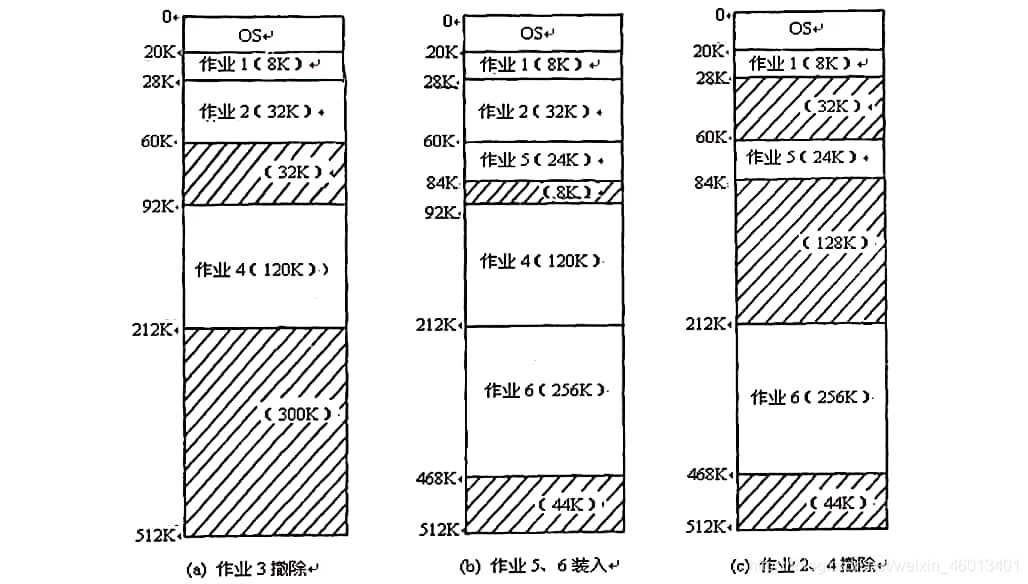
二、可变分区的分配

可变分区分配算法：

①首次适应算法：

原理：要求空闲分区链以地址递增的次序链接，在进行内存分配时，从链首开始顺序查找，直至找到一个能满足其大小要求的空闲分区为止。

特点：该算法倾向于优先使用内存中低址部分，为的是保留了高址部分的大空闲区，为得是以后为大程序分配大内存空间。

缺点：每次都是在低址部分划分区域，所以会留下许多难以利用、很小的空闲分区，被称为内存碎片。而且每一次的查找都是从低址部分开始的，会增加查找可用空闲分区的开销。

②循环首次适应算法：

在为作业分配内存空间时，不再每次从链首开始查找，而是从上次找到的空闲分区的下一个空闲分区开始查找。直至找到第一个能满足要求的空闲分区。

③最佳适应算法：

把既能满足要求、又是最小的空闲分区分配给作业。为了加速查找到适用的最小空闲分区，该算法会将所有的空闲区按照分区的大小以递增的顺序形成一空闲分区链表。

但是这个算法也存在一个弊端——每次分配空闲空间之后所切割下的剩余部分总是最小的，更容易形成内存碎片。

④最差适应算法：

每次为作业分配内存时，总是找到一个满足作业长度要求的最大空闲分区进行分配。这样剩下来的空闲区不至于太小而形成内存碎片。

这种算法适用于中、小程序；但是对于大程序的运行来讲是不利的。（因为你每次都将大的空闲空间用掉，这样下去当你想让大程序进入内存的时候就很难找到放的下的内存空闲空间了！）

 

可变分区分配操作：

• 设请求的分区大小为u.size，表中每个空闲分区的大小可表示为m.size。
• 系统要利用某种分配算法（首次、循环首次、最佳、最差），从空闲分区表/链中找到所需的适合分区。
• 若m.size-u.size小于系统规定的最小值，则将整个分区分配给请求者；否则从该分区中划分出与请求的大小相等的内存空间分配出去。余下的部分仍留在空闲分区表或空闲分区链中。修改相应的数据结构。
• 将分配区的首址返回给调用者

---

 

三、可变分区的回收：

可变分区回收操作：

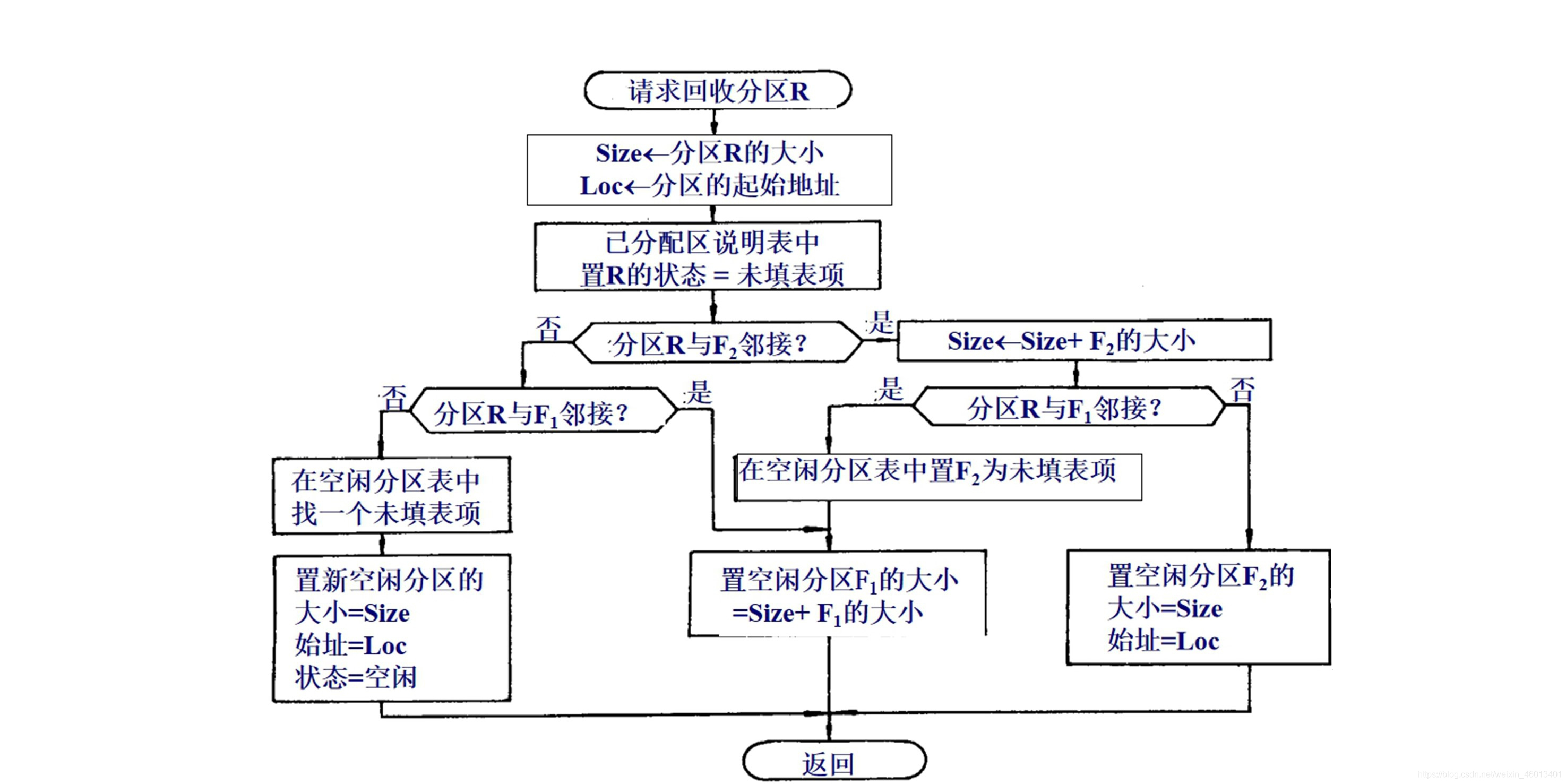
当作业运行完毕释放内存时，系统根据回收区的首址，从空闲分区表（链）中找到相应的插入点，进行回收，此时可能出现以下四种情况（个人理解：有相邻则合并，无相邻则单独为一区！）：

——回收区与插入点的前一个分区相邻接，两分区合并。

——回收区与插入点的后一个分区相邻接 ，两分区合并。

——回收区同时与插入点的前、后两个分区邻接 ，三分区合并。

——回收区与插入点前、后两个分区都不相邻 ，单独一个分区。

可变分区回收示意图

 

可变分区内存回收算法：

假定作业归还的分区起始地址为S，长度为L，则：

① 归还区有下邻空闲区：如果S+L正好等于空闲区表中某个登记栏目（假定为第j栏）的起始地址，则表明归还区有一个下邻空闲区。

• 这时只要修改第j栏登记项的内容： 起始地址=S； 第j栏长度=第j栏长度+L。

② 归还区有上邻空闲区：如果空闲区表中某个登记栏目（假定为第k栏）的“起始地址+长度”正好等于S，则表明归还区有一个上邻空闲区。

• 这时要修改第k栏登记项的内容（起始地址不变）： 第k栏长度=第k栏长度+L；

③ 归还区既有上邻空闲区又有下邻空闲区：如果S+L正好等于空闲区表中某个登记栏目（假定为第j栏）的起始地址，同时还有某个登记栏目（假定为第k栏）的“起始地址+长度”正好等于S，这表明归还区既有一个上邻空闲区又有一个下邻空闲区。

• 此时对空闲区表的修改如下： 第k栏长度=第k栏长度+第j栏长度+L；（第k栏起始地址不变） 第j栏状态=“空”；（将第j栏登记项删除）

④ 归还区既无上邻空闲区又无下邻空闲区：如果在检查空闲区表时，无上述三种情况出现，则表明归还区既无上邻空闲区又无下邻空闲区。这时，应该在空闲区表中查找一个状态为“空”的栏目（假定查到的是第t栏）。

• 则第t栏的内容修改如下：     第t栏起始地址=S；     第t栏长度=L；     第t栏状态=“未分配”

可变分区的回收算法

---

 

四、可变分区分配的优缺点：

优点：有助于多道程序设计，提高了内存的利用率、要求硬件支持少，代价低、管理算法简单，实现容易。

缺点：必须给作业分配一连续的内存区域、碎片问题严重，内存仍不能得到充分利用、不能实现对内存的扩充。

 

Ending... ...