【数值计算方法】数值积分&微分-python实现-p1

原文链接：https://www.cnblogs.com/aksoam/p/18332123
更多精彩，关注博客园主页，不断学习！不断进步！

我的主页

csdn很少看私信，有事请b站私信

博客园主页-发文字笔记-常用

有限元鹰的主页 内容：

1. ABAQUS数值模拟相关
2. Python科学计算
3. 开源框架，编程学习笔记

哔哩哔哩主页-发视频-常用

FE-有限元鹰的个人空间 内容：

1. 模拟案例
2. 网格划分
3. 游戏视频，及其他搬运视频

数值积分

1. 引言

高数中计算积分思路基本是牛顿莱布尼兹法:

$$I[f]={\int }_a^{b}f(x)\mathrm{d}x=F(b)-F(a),$$

$$F^{\prime }(x)=f(x).$$

实际计算中,原函数一般无法求出.给不出解析解,只能求出数值解.

设在区间 [a,b]( 不妨先设 a,b 为有限数 ) 上 ,$f(x)\approx P_n(x),P_n(x)$ 为某个较“简单”的函数 , 则显然有

$${\int }_a^{b}f(x)\mathrm{d}x\approx {\int }_a^b{P}_n(x)\mathrm{d}x.$$

如果${\max }_{a⩽x⩽b}|f(x)-P_n(x)|⩽\epsilon$,则误差估计:

$$\left|{\int }_a^{b}f(x)\mathrm{d}x-{\int }_a^b{P}_n(x)\mathrm{d}x\right|⩽(b-a)\epsilon .$$

2. 几个常用积分公式及其复合公式

• 中点公式

对f(x),使用$f(\frac{a+b}{2})$近似代替.有:

$${\int }_a^{b}f(x)\mathrm{d}x\approx {\int }_a^{b}f\left(\frac{a+b}{2}\right)\mathrm{d}x=(b-a)f\left(\frac{a+b}{2}\right).\text{\hspace{1em}(1)}$$

误差估计:

$${\int }_a^{b}f(x)\mathrm{d}x-(b-a)f\left(\frac{a+b}{2}\right)=\frac{1}{12}(b-a{)}^3{f}^{\prime \prime }(\xi ).$$

• 梯形公式

拉格朗日插值多项式$L_n(x)$:

$$L_n(x)=\sum _{j=0}^n{y}_j{l}_j(x)=\sum _{j=0}^n{y}_j\prod _{\begin{array}{c}i=0\\ i\ne j\end{array}}^n\frac{x-x_i}{x_j-x_i}.$$

$n=1$时,$L_1(x)=l_0(x)y_0+l_1(x)y_1$,用$L_1(x)$ 近似代替 f(x) 称为线性插值 , 公式(3.9)称为线性插值多项式或一次插值多项式.即:

$$L_1(x)=\frac{x-x_1}{x_0-x_1}{y}_0+\frac{x-x_0}{x_1-x_0}{y}_1.$$

$n=2$时,$L_2(x)=l_0(x)y_0+l_1(x)y_1+l_2(x)y_2$,用$L_2(x)$近似代替 f(x) 称为二次插值或抛物线插值 , 称式 (3.10) 为二次插值多项式

$$L_2(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}{y}_0+\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}{y}_1+\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}{y}_2$$

基于$x=a,x=b$两节点构造线性插值函数$L_1(x)$,近似代替原函数$f(x)$,得到梯形公式.

$$L_1(x)=\frac{x-b}{a-b}f(a)+\frac{x-a}{b-a}f(b)$$

$$\begin{array}{rl}{\int }_a^{b}f(x)\mathrm{d}x& \approx {\int }_a^b{L}_1(x)\mathrm{d}x={\int }_a^b\left[\frac{x-b}{a-b}f(a)+\frac{x-a}{b-a}f(b)\right]\mathrm{d}x\\ & =\frac{1}{2}(b-a)\left[f(a)+f(b)\right].\end{array}\text{\hspace{1em}(2)}$$

误差估计:

$${\int }_a^{b}f(x)\mathrm{d}x-\frac{1}{2}(b-a)\left[f(a)+f(b)\right]=-\frac{1}{12}(b-a{)}^3{f}^{\prime \prime }(\xi ),\xi \in (a,b)$$

• 辛普森 (Simpson) 公式(抛物型公式)

$\text{若 }f(x)\text{ 用通过节点 }{x}_0=a,x_1=\frac{a+b}{2},x_2=b\text{ 的二次插值多项式 }{L}_2(x)\text{ 代替}$

$$f(x)\approx L_2(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}f(x_0)+\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}f(x_1)+\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}f(x_2)$$

可以得到积分公式:

$${\int }_a^{b}f(x)\mathrm{d}x\approx {\int }_a^b{L}_2(x)\mathrm{d}x=\frac{1}{6}(b-a)\left[f(a)+4f\left(\frac{a+b}{2}\right)+f(b)\right].\text{\hspace{1em}(3)}$$

误差估计:

$${\int }_a^{b}f(x)\mathrm{d}x-\frac{1}{6}(b-a)\left[f(a)+4f\left(\frac{a+b}{2}\right)+f(b)\right]=-\frac{(b-a{)}^5}{2880}{f}^{(4)}(\xi ),\xi \in (a,b).$$

2.1 求积公式

回顾以上三个积分公式,可以看出:一般地 , 若已知函数 f(x) 在区间 [a,b] 内节点$x_0,x_1,\cdot \cdot \cdot ,x_n$上的值$f(x_0),f(x_{)},\cdot \cdot \cdot ,f(x_n)$, 则称形如

$${\int }_a^{b}f(x)\mathrm{d}x\approx \sum _{i=0}^n{\omega }_{i}f(x_i)$$

的式子为求积公式 , 其中 $x_i$ 称为求积节点 , ${\omega }_i$称为求积系数 . 求积节点及求积系数不依赖于被积函数 f(x) 的具体形式 .

记$Q[f]={\sum }_{i=0}^n{\omega }_{i}f(x_i),$则误差(余项)为:$R[f]=I[f]-Q[f].$

2.2 代数精度

定义 5.2.1 如果对所有次数小于等于 m 的多项式 f(x), 等式

$${\int }_a^{b}f(x)\mathrm{d}x=\sum _{i=0}^n{\omega }_{i}f(x_i)$$

成立 , 但对某个次数为 m + 1 的多项式 f(x),等式不精确成立 , 则称求积公式 (5.8) 的代数精度为 m 次

代数精度适用于判断求积公式好坏的标准之一.如何计算公式代数精度如下做法:

• 以中点公式为例

中点公式的误差估计(余项)为$R[f]=\frac{1}{12}(b-a{)}^3{f}^{\prime \prime }(\xi ),\xi \in (a,b),$,当f(x)分别取$1,x,x^2$时,有

$$R[f]=0,0,\frac{1}{6}(b-a{)}^3$$

所以,中点公式的代数精度为$m=1$.

• 另一种方式

将$1,x,x^2,\cdot \cdot \cdot ,x^{m+1}$分别代入求积公式两边,分别计算,对比.直到m+1次幂时等式不成立,则称求积公式的代数精度为m次.

2.3 复合积分

在通常情况下 , 积分区间 [a,b] 的长度 b−a 不是非常小 , 因此为了确保计算精度 , 通常采用复合求积公式

复合积分 , 就是将积分区间分为若干份 , 在每一个 “ 小区间 ” 上用低阶求积公式 (1),(2) 或 (3) 进行计算 , 再将计算值相加即得原积分的近似值

将积分区间 [a,b] 分为 n 等分 , 记步长$h=\frac{b-a}{n}$,节点为 $x_i=a+ih(i=0,1,\cdots ,n),$并记$x_{i+\frac{1}{2}}=\frac{1}{2}(x_i+x_{i+1})$,根据定积分形式

$${\int }_a^{b}f(x)\mathrm{d}x=\sum _{i=0}^{n-1}{\int }_{x_i}^{x_{i+1}}f(x)\mathrm{d}x,$$

当n取值足够大,即$h$足够小,在每个区间应用低阶积分公式,就得到了复合积分公式.

• 复合中点公式

$${\int }_a^{b}f(x)\mathrm{d}x\approx \sum _{i=0}^{n-1}hf\left(x_{i+\frac{1}{2}}\right)\triangleq M_n\text{\hspace{1em}(4)}$$

• 复合梯形公式

$$\begin{array}{rl}{\int }_a^{b}f(x)\mathrm{d}x& \approx \sum _{i=0}^{n-1}\frac{h}{2}\left[f(x_i)+f(x_{i+1})\right]\\ & =\frac{h}{2}\left[f(a)+2\sum _{i=1}^{n-1}f\left(x_i\right)+f(b)\right]\triangleq T_n.\end{array}\text{\hspace{1em}(5)}$$

• 复合辛普森公式

$$\begin{array}{rl}{\int }_a^{b}f(x)\mathrm{d}x& \approx \sum _{i=0}^{n-1}\frac{h}{6}\left[f(x_i)+4f(x_{i+\frac{1}{2}})+f(x_{i+1})\right]\\ & =\frac{h}{6}\left[f(a)+4\sum _{i=0}^{n-1}f(x_{i+\frac{1}{2}})+2\sum _{i=1}^{n-1}f(x_i)+f(b)\right]\triangleq S_n.\end{array}\text{\hspace{1em}(6)}$$

三个公式的误差余项分别为:

$$\begin{array}{rl}{R}_M=& {\int }_a^{b}f(x)\mathrm{d}x-M_n=\sum _{i=0}^{n-1}{\int }_{x_i}^{x_{i+1}}f(x)\mathrm{d}x-\sum _{i=0}^{n-1}hf(x_{i+\frac{1}{2}})\\ =& \sum _{i=0}^{n-1}\frac{1}{12}{h}^3{f}^{\prime \prime }(\xi ).\end{array}$$

$$R_T={\int }_a^{b}f(x)\mathrm{d}x-T_n=-\frac{1}{12}(b-a)h^2{f}^{\prime \prime }(\eta ),\eta \in (a,b),$$

$$R_S={\int }_a^{b}f(x)\mathrm{d}x-S_n=-\frac{1}{2880}(b-a)h^4{f}^{(4)}(\eta ),\eta \in (a,b).$$

2.4 常用积分公式的python实现

6种常用积分公式的python实现如下:

展开查看代码

# -*- coding: utf-8 -*-
# 数值计算方法实现(python)
import numpy as np
from typing import List, Tuple,Union

### y = 4/( 1+x^2 )
# f= lambda x: 4/( 1+x**2 )

def MidPointInteg1d(f, a:float, b:float)->float:
    """一维中点积分公式"""
    return (b-a)*f((a+b)/2)

def ComMidPointInteg1d(f, a:float, b:float, n:int)->float:
    """一维复合中点积分公式"""
    h=(b-a)/n
    x=np.linspace(a+0.5*h,b-0.5*h,n)
    return h*sum([f(xi) for xi in x])

def trapezoidInteg1d(f, a:float, b:float)->float:
    """一维梯形积分公式"""
    return (b-a)*(f(a)+f(b))/2.0

def ComtrapezoidInteg1d(f, a:float, b:float, n:int)->float:
    """一维复合梯形积分公式"""
    h=(b-a)/n
    # x_i  (i=0,1,...,n)
    x=[a+i*h for i in range(n+1)]
    return 0.5*h*(-f(a)-f(b)+2*sum([f(xi) for xi in x]))

def SimpsonInteg1d(f, a:float, b:float)->float:
    """一维 Simpson 积分公式"""
    return (b-a)*(f(a)+4*f((a+b)/2.0)+f(b))/6.0

def ComSimpsonInteg1d(f, a:float, b:float, n:int)->float:
    """一维复合 Simpson 积分公式"""
    h=(b-a)/n
    # x_i  (i=0,1,...,n)
    x=[a+i*h for i in range(n+1)]
    t1=sum([f(0.5*(x[i]+x[i+1])) for i in range(0,n)])
    t2=sum([f(x[i]) for i in range(1,n)])
    return (h/6.0)*(f(a)+f(b)+4*t1+2*t2)

def integ1d(f:object, 
            a:float, 
            b:float,
            **kwargs)->float:
    """一维数值积分"""
    if kwargs['method']==1:
        return MidPointInteg1d(f, a, b)
    if kwargs['method']==2:
        return trapezoidInteg1d(f, a, b)
    if kwargs['method']==3:
        return SimpsonInteg1d(f, a, b)

def ComInteg1d(f, 
                a:float, 
                b:float, 
                n:int,
                **kwargs)->float:
    """一维复合积分"""
    if kwargs['method']==1:
        return ComMidPointInteg1d(f, a, b, n)
    if kwargs['method']==2:
        return ComtrapezoidInteg1d(f, a, b, n)
    if kwargs['method']==3:
        return ComSimpsonInteg1d(f, a, b, n)
    
def showError(Numerical:float, Exact:float)->None:
    """显示误差"""
    print(f"数值解: {Numerical}, 精确解: { Exact}, 误差: {0.01*(Exact-Numerical)}%")
    

验证:

展开查看代码

# f(x)=e^(-x)
f=lambda x: np.exp(-x)
accVal=0.6321

# 积分范围
a,b=0,1

# 计算积分
integ1=integ1d(f,a,b,method=1)
integ2=integ1d(f,a,b,method=2)
integ3=integ1d(f,a,b,method=3)

print(f"中点积分：{integ1}")
showError(integ1,accVal)

print(f"梯形积分：{integ2}")
showError(integ2,accVal)

print(f"Simpson积分: {integ3}")
showError(integ3,accVal)

输出:
中点积分：0.6065306597126334
数值解: 0.6065306597126334, 精确解: 0.6321, 误差: 0.0404514163698253
梯形积分：0.6839397205857212
数值解: 0.6839397205857212, 精确解: 0.6321, 误差: -0.08201189777839135
Simpson积分: 0.6323336800036626
数值解: 0.6323336800036626, 精确解: 0.6321, 误差: -0.0003696883462468591

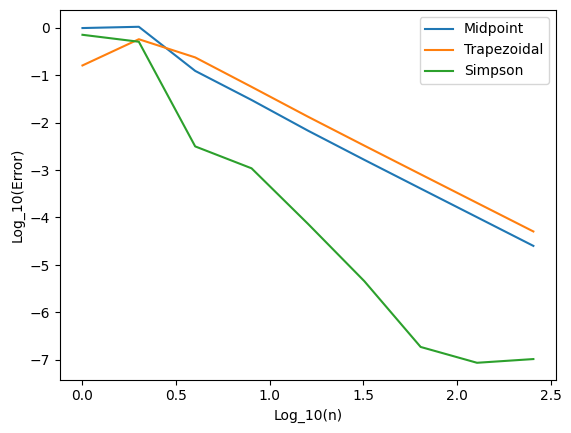
步长数目越多,误差越小.

展开查看代码

f2= lambda x: x*np.exp(-1*x)*np.cos(2*x)

# 积分范围
a,b=0,2*np.pi
n =[2**i for i in range(9)]
extract=-0.122122499

e1,e2,e3=[],[],[]
# 复合积分计算
for ni in n:
    integ_mid=ComInteg1d(f2,a,b,ni,method=1)
    integ_trap=ComInteg1d(f2,a,b,ni,method=2)
    integ_simpson=ComInteg1d(f2,a,b,ni,method=3)
    e1.append(abs(integ_mid-extract))
    e2.append(abs(integ_trap-extract))
    e3.append(abs(integ_simpson-extract))

from matplotlib import pyplot as plt
plt.plot(np.log10(n),np.log10(e1),label='Midpoint')
plt.plot(np.log10(n),np.log10(e2),label='Trapezoidal')
plt.plot(np.log10(n),np.log10(e3),label='Simpson')
plt.xlabel('Log_10(n)')
plt.ylabel('Log_10(Error)')
plt.legend()
plt.show()

3. 变步长方法与外推加速技术

复合中点公式、梯形公式以及辛普森公式都是有效的求积方法 , 步长 h 越小 ,
计算精度越高 . 但在实际运用上述求积公式进行计算时须事先选取一个合适的步长 h,**因此在给定计算精度的情形下 , 往往通过不断调整步长的方式进行计算 **

• 变步长梯形法

在实际计算中往往会采用让步长逐次折半的方式 , 反复使用复合求积公式进行计算 , 直至相邻两次计算结果之差的绝对值小于给定的计算精度为止 . 这种方法即称为变步长算法

变步长梯形方法的优点是算法简单 , 编程容易 ; 缺点是收敛速度较慢

python version

def VarStepInteg1d(f, a:float, b:float,precision:float=1e-5,
                    **kwargs)->float:
    """一维变步长积分"""
    k=0
    Tn=ComInteg1d(f, a, b, 1, method=kwargs['method'])
    print(f"第0次积分, 步长: {(b-a)/(2**k)}, 结果: {Tn}")
    while True:
        k+=1
        T2n=ComInteg1d(f, a, b, 2**k, method=kwargs['method'])
        print(f"第{k}次积分, 步长: {(b-a)/(2**k)}, 结果: {T2n}")
        if abs(T2n-Tn)<=precision:
            print(f"精度要求达到, 迭代次数: {k}, 步长: {(b-a)/(2**k)}")
            return T2n
        else:
            Tn=T2n

f3=lambda x: np.sin(x)/x if x!=0 else 1

# 积分范围
a,b=0,1

# 计算积分
VarStepInteg1d(f3,a,b,1e-7,method=2)

# 输出:
# 第0次积分, 步长: 1.0, 结果: 0.9207354924039483
# 第1次积分, 步长: 0.5, 结果: 0.9397932848061772
# 第2次积分, 步长: 0.25, 结果: 0.9445135216653895
# 第3次积分, 步长: 0.125, 结果: 0.9456908635827014
# 第4次积分, 步长: 0.0625, 结果: 0.945985029934386
# 第5次积分, 步长: 0.03125, 结果: 0.9460585609627681
# 第6次积分, 步长: 0.015625, 结果: 0.946076943060063
# 第7次积分, 步长: 0.0078125, 结果: 0.9460815385431518
# 第8次积分, 步长: 0.00390625, 结果: 0.9460826874113473
# 第9次积分, 步长: 0.001953125, 结果: 0.9460829746282345
# 第10次积分, 步长: 0.0009765625, 结果: 0.9460830464324462
# 精度要求达到, 迭代次数: 10, 步长: 0.0009765625

• 外推加速技术与龙贝格求积方法

讲义链接

4. 牛顿-科茨公式(Newton-Cotes formula)

中点公式、梯形公式及辛普森公式可分别看成是 f(x) 用常数、线性插值函数和抛物型插值函数代替再积分所得 . 若将此想法进一步推广 , 将 f(x) 用 n + 1 个等距节点上的 n 次拉格朗日插值多项式代替 , 即得所谓的牛顿–科茨 (Newton-Cotes) 公式.

设 $x_i=a+ih,h=\frac{b-a}{n},$作 f(x) 的 n 次拉格朗日插值多项式 $L_n(x)$.为方便起见 , 令$x=a+th,t\in [0,n],$则 $L_n(x)$ 可表示为

$$L_n(x)=\sum _{i=0}^n\frac{(-1{)}^{n-i}}{i!(n-i)!}\prod _{j=0,j\ne i}^n(t-j)f(x_i),$$

$${\int }_a^{b}f(x)\mathrm{d}x\approx {\int }_a^b{L}_n(x)\mathrm{d}x=\sum _{i=0}^n{\omega }_{i}f(x_i).$$

求积系数${\omega }_i$的为:

$$\begin{array}{rl}{\omega }_i=& (b-a)\frac{(-1{)}^{n-i}}{ni!(n-i)!}{\int }_0^n\prod _{j=0,j\ne i}^n(t-j)\mathrm{d}t\\ =& (b-a)C_i^{(n)},\end{array}$$

$$C_i^{(n)}=\frac{(-1{)}^{n-i}}{ni!(n-i)!}{\int }_0^n\prod _{j=0,j\ne i}^n(t-j)\mathrm{d}t,$$

$C_i^{(n)}$为科茨系数,仅与区间节点数目及第 i 个节点有关 .

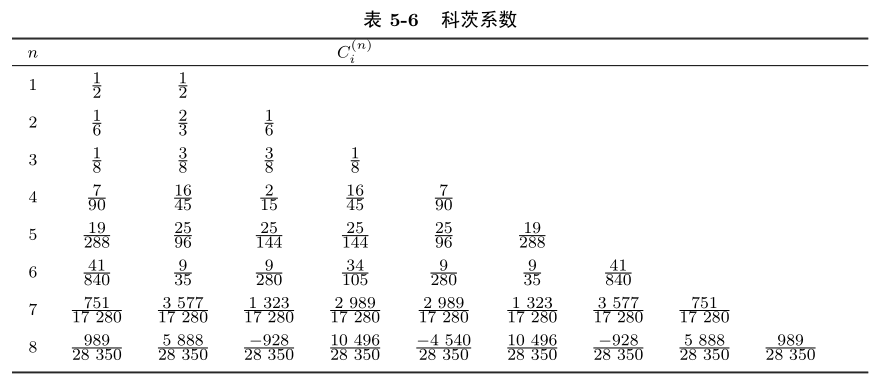
n > 8 时科茨系数有正有负 , 此时对应的求积公式的稳定性得不到保证 . 且由于对高次插值多项式来说 , 收敛性一般不成立 , 故在实际计算中一般不采用高阶的牛顿 – 科茨公式(n > 8).

定理5.4.1: 当 n 为奇数时 , 牛顿 – 科茨公式 (5.23) 的代数精度至少为 n 次 ; 而当 n 为偶数时 , 代数精度至少为 n + 1 次 .

该求积公式是稳定的.而当n>7时，由于求积系数，有正有负，因此稳定性一般不成立，收敛性一般也不成立.因此对高阶牛顿科茨公式，

牛顿 – 科茨公式误差$R[f]$为:

$$\begin{array}{rl}R[f]=& h^{n+2}{\int }_0^n\prod _{i=0}^n(n-i-s)\mathrm{d}s\\ =& (-1{)}^{n+1}{h}^{n+2}{\int }_0^n\prod _{i=0}^n[s-(n-i)]\mathrm{d}s.\end{array}$$

尽管它具有较高的代数精度，一般不采用.常用的是中点公式、梯形公式和抛物型公式的复合求积公式以及下节的采用非等分节点的高斯(Gauss)公式

newton-cotes 公式的python实现

def Integ1dNewtonCotes(f,a:float,b:float,n:int)->float:
    """给定n(>=1)个点,计算一维牛顿-科特斯积分"""
    if n<=0:
        raise ValueError("牛顿-科特斯积分时,n最小值为1")
    weights=NewtonCotes_weights(a,b,n)
    h=(b-a)/n
    x=[a+i*h for i in range(n+1)]
    return sum([weights[i]*f(x[i]) for i in range(n+1)])

# check ok
def NewtonCotes_factor(i:int,n:int)->float:
    """计算牛顿-科特斯积分的第i个权重"""
    import math
    import numpy as np
    def f(t:float):
        s=1.0
        for j in range(n+1):
            if j==i:
                continue
            s=s*(t-j)
        return s
    t1=((-1)**(n-i))/(n*math.factorial(i)*math.factorial(n-i))
    t2=Integ1dGuassLegendre(f,0,n)
    return t1*t2

def NewtonCotes_weights(a:float,b:float,n:int=10)->List[float]:
    """计算牛顿-科特斯积分的权重数组"""
    weights=[(b-a)*NewtonCotes_factor(i,n) for i in range(n+1)]
    return np.array(weights)