插头DP && 概率DP / 期望DP

写在前面：

  快开学了，先发下最近整理的DP，还有过年前学的状压DP、记忆化搜索等基础DP还有图论等知识还在整理中…
  由于本人平时比较懒，所以把十几道题都弄在一篇博客，这篇博客比较长，近3万字，但我相信大家还是能看懂我在说什么的。

插头DP

P5056 【模板】插头dp

  有些状压DP问题要求我们记录状态的连通性信息，这类问题一般被形象的称为插头DP或连通性状态压缩DP。插头dp是基于连通性状态压缩的动态规划，一般的适用范围：数据范围小，并且处于网格图中，对连通性有要求（要求选择出来的格子是一个连通块或者是一个路径/回路）。这样说起来很抽象，我先介绍一道插头dp的模板题：
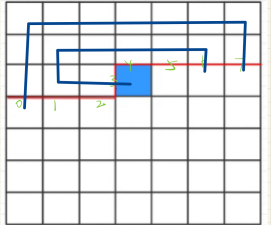
  给我们一个n * m的棋盘，这个棋盘里面有些格子是障碍，有些格子是空格，求这个棋盘有多少个不同的哈密顿回路（要经过每个格子，并且每个格子只能经过一遍），我们来简单回顾一下哈密顿回路的做法：先用一个状态S表示我们当前已经走过哪些点，另外用i表示我们当前走到了哪个点，然后枚举下一个点是哪一个点，假设下一个点是j，f(s, i)就变成了f(s | 1 << j, j)，此时的时间复杂度是2ⁿ * n²，现在是一个棋盘，如果按照这种做法来做时间复杂度会太大。棋盘有个特点：每个格子只能和上下左右四个格子相连，并不是能和任意格子相连，所以可以按照一行一行来枚举所有状态（对于一般图我们就不能这样），我们递推的时候一般是按格来递推，举个例子，我们要考虑这个格子，这也意味着我们已经考虑完了这个红色线上方的格子，所以此时我们只要分析这个格子的状态就可以了。

  因为我们要组成一个回路，所以每个格子只能有两条边会被经过，假设有一个边是进来的，有一个边是出去的，也就是在它的四条边里边选两条边经过，这样经过每个格子有6种情况，对于整一个连通块，我们只关心它轮廓线上的状态（即每条边有没有线经过），还要维护轮廓线上方部分的连通性（经过轮廓线的边哪些是属于同个连通块的）

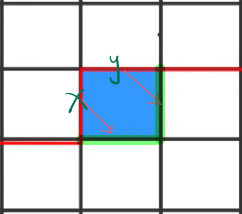
  （上面0和7，3和6就是属于同一个连通块）记录连通块一般有两种方法：1、最小表示法，从左往右遍历轮廓线，当遍历到没被标记的边（且有路径要经过它）的时候，按顺序标记，所以0和7标记成1，3和6标记成2（属于同个连通块标记相同），所以此时轮廓线的状态：10020021。2、括号表示法，括号表示法的适用范围要小一些，但效率更高（首选），因为我们要找的是一个哈密顿回路，这就意味着上半部分有一条边上去，就一定有一条边下来，这些边必然是两两配对的，而且这两条边之间的连通块是不可能交叉的（两条边所连的路径不可能交叉），因为是相邻的两两配对，所以可以看做是若干个括号，我们用1表示“左括号”，用2表示有括号，用一个三进制的数就能表示轮廓线的状态，所以此时轮廓线的状态：10010022。
  这道题用括号表示法比用最小表示法的优势是，我们用012就可以表示轮廓线的状态，而最小表示法要用到的数可能很大（有多少个连通块，最大就是多少）。另外，括号表示法每一位就012，可以把它看成是4进制，然后在更新状态的时候就可以用位运算去优化。
  状态表示是三维，f[i, j, s]表示当遍历到第i行第j列的格子的时候分界线的状态是s时，所有方案的数量，s有效的状态是4、5万个（因为它要满足1和2是两两配对的）。插头dp比较麻烦的就是状态转移，我们把目标格子(g[i, j])在轮廓线上的边标记成x和y，轮廓线上的状态为state，需要分成以下几种情况（转移的过程中x对应格子下面的边，y对应格子右边的边）：
  1、g[i, j]是障碍物，x和y一定是0，且这个格子也不会有路径经过，所以state不变(x和y都是0，转移之后也是0)

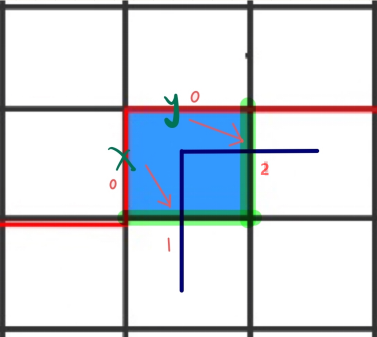
接下来g[i, j]不是障碍物的情况：
  2、x和y均为0，更新后state中x = 1, y = 2

  3、x为0，y非0，更新后state中状态不变或者x = y, y = 0


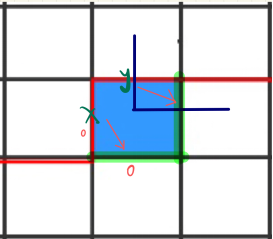
  4、x非0，y为0，更新后state中y = x, x = 0或者状态不变


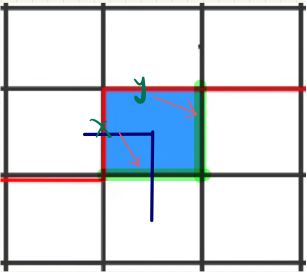
  5、x = y = 1，x和y相连，此时state中原来x和y的位置变成0，然后离y最近的2变成1，又因为格子已经有两条边了，所以更新之后x和y对应的位置为0。

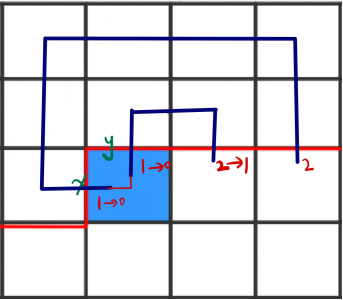
  6、x = y = 2，x和y相连，此时state中原来x和y的位置变成0，然后离x最近的1变成2，又因为格子已经有两条边了，所以更新之后x和y对应的位置为0。

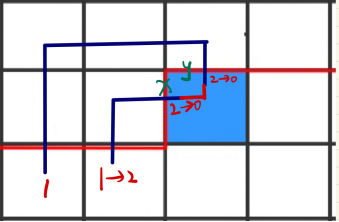
  7、x = 2, y = 1，x与其前面第一个1配对，y与后面第一个2配对，更新后state中x = 0, y = 0。

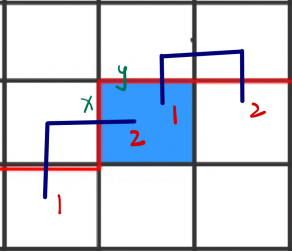
  8、x = 1, y = 2，x是某个路径的左半边，y是某个路径的右半边，又因为x和y在轮廓线中是相邻的，所以x和y是属于同一个路径的，这种情况只会发生在最后一个合法的格子。
  接下来分析数据，在f[i, j, s]中s是轮廓线的状态，因为我们是用四进制来表示三进制，而4的13次方是等于67108864，而有效的状态只有4w多个，所以插头dp在存状态的时候一般是用哈希表来存的，而且哈希表最好不要用stl中的哈希表，因为插头dp的常数比较大，题目卡得比较严，所以现在我们要手写哈希表…

手写哈希表的方法：

  1、开放寻址法
  2、拉链法
  哈希表的作用：从较庞大的空间/值域，把它映射到一个较小的空间(0 ~ N)。
  结合这道题来介绍手写哈希表的两种做法：

  当要存储的数是x时，我们可以构造一个哈希函数h(x)，这个函数它可以把-10⁹ ~ 10⁹的一个数映射到0 ~ 10⁵之间的一个数，通常会采取x % 10⁵的做法，值域比较大，但是映射的结果比较小，所以必然会产生冲突，也就是我们可能会把两个相同的数映射成同一个数，对于冲突的解决方式可以采用两种方法(开放寻址法/拉链法)。
  拉链法：
  先开一个长度为10⁵的数组，当两个数发生冲突的时候，就在某个位置i拉下一条链，把之前的数放在链的第一个位置，然后把新得到的数放在i位置，类似于对于某一个数组元素接一个邻接表。哈希算法是一种期望算法，虽然说每一个位置都有可能拉下来一条链，但是在平均情况下，每一条链的长度可以看成是常数，所以哈希表的时间复杂度可以看成O(1)。
  我们在建立一个哈希表的长度的时候一般取成一个质数（就是取模的数），而且这个质数要离2的n次方尽可能远。定义h[N]哈希数组，对于每一个“槽”，我们要向下拉一条链（类似于之前的链表），链表要存两个东西，一个是它的值e[idx]，另一个是下一个值的下标ne[idx]，具体做法和对链表的插入查找相同。

拉链法的代码如下：

const int N = 100003;
	int h[N], e[N], ne[N], idx;
	int insert(int x){
   
		int k = (x % N + N) % N;
		e[idx] = x;
		ne[idx] = h[k];
		h[k] = idx++; 
	}
	int find(int x){
   
		int k = (x % N + N) % N;
		for(int i = h[k]; i != -1; i = ne[i]){
   
			if(e[i] == x) return 1;
		}
		return 0;
	}
	int main(){
   
	    int n, m;
	    cin >> n;
	    char p[2];
	    memset(h, -1, sizeof(h));
	    while(n--){
   
	    	scanf("%s%d", p, &m);
	    	if(p[0] == 'I') insert(m);
	    	else{
   
	    		if(find(m)) cout << "Yes\n";
				else cout << "No\n";
			} 
		}
	    return 0;
	}

  开放寻址法：
  它只开了一个一维数组，一维数组的长度一般要开到题目数据范围的两到三倍(这道题开到20w ~ 30w)，这样的话冲突的概率就小一点。开放寻址法就像我们去厕所找坑位，我想要的坑位有人了，就按顺序看看下一个空位有没有人，以此类推，直到找到坑位为止。

开放寻址法的代码如下：

const int N = 200003, null = 0x3f3f3f3f;
int find(int x){
   
	int k = (x % N + N) % N;
	while(h[k] != null && h[k] != x){
   
		k++;
		if(k == N) k = 0;
	}
	return k;
}
int main(){
   
    int n, m;
    cin >> n;
    char p[2];
    memset(h, 0x3f, sizeof(h));
    while(n--){
   
    	scanf("%s%d", p, &m);
    	if(p[0] == 'I') h[find(m)] = m;
    	else{
   
    		if(h[find(m)] == null) cout << "No\n";
			else cout << "Yes\n";
		} 
	}
    return 0;
}

  言归正传，我在插头dp这道题用开放寻址法，另外，这个题目合法状态大约4w多个，估算一下5w * 144（格子数），大概是700多w个状态，有些题目的数量可能更多，所以要用到滚动数组。由于对于每个格子，总共的状态有6k多w个，合法状态只有不到5w个，我们去枚举的时候就没必要去枚举所有状态，而要用一个数组先存储每一次滚动的有效状态。估算下时间复杂度：f[i, j, s]假设所有有效状态数量是S(最多不到5w)，再乘以i、j(n²)，然后再算状态的时候，对于5和6的情况，我们是需要枚举找出与某条边配对的边，最坏情况下是需要O(N)的计算量，所以整个算法的时间复杂度就是S * n³，大概是5w * 12 * 12 * 12 = 8.64 * 10⁷，但本质上来说没有这么高（有效状态不到5w，也不是所有状态都要枚举8种情况），这就是插头dp的具体思路。

接下来是这道题的代码实现：

  （具体有点复杂，为了大家方便理解，我每一行我都加了注释，虽然我自己都觉得有点恶心…）

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <string>
#include <cstring>
#include <map>
#include <queue>
using namespace std;
typedef long long LL;
 
void debug_out(){
   
    cerr << endl;
}
template<typename Head, typename... Tail>
void debug_out(Head H, Tail... T){
   
    cerr << " " << to_string(H);
    debug_out(T...);
}
#ifdef local
#define debug(...) cerr<<"["<<#__VA_ARGS__<<"]:",debug_out(__VA_ARGS__)
#else
#define debug(...) 55
#endif
using namespace std;
const int N = 50005, M = N * 2 + 7;
//状态数量，3^13 ~ 6000万个，有效的大概为4万~5万个
//开放寻址法的数组通常是2~3倍，同时取成质数，用于取模
int g[15][15], q[2][N], cnt[2], h[2][M], ex, ey; 
//g是判断是不是障碍物
//q是滚动数组，存储的是某个有效状态对应在哈希表的下标
//h是滚动数组，滚动hash表，第二维是哈希值的位置，存储的是哈希表某个下标对应的具体有效状态（哈希值） 
//cnt数组是每一次滚动过程中（当前格子）有效状态的数量 
LL v[2][M], ans;
//v是有效状态对应的方案数，ans累加所有方案数 
int set(int k, int v){
   	//构造四进制的第k位数字为v的数字
	return v * (1 << k * 2);
}
int get(int state, int k){
    //求第k个格子的状态,四进制的第k位数字
	return state >> (k * 2) & 3; 
}
int find(int cur, int x){
   	//开放寻址法找到给有效状态存储的哈希表下标 
	int t = x % M;	//取模找到预定存储的位置 
	while(h[cur][t] != -1 && h[cur][t] != x){
   	//直到找到空位置或者发现已经存过了 
		if(++t == M) t = 0;	//在按顺序寻找空位置的过程中，要是到了数组的右边界，就回到数组的头部再找 
	}
	return t;	//返回有效状态存储的哈希表下标 
}
int insert(int cur, int state, LL w){
   	//在滚动哈希表中新加入有效状态 
	int t = find(cur, state);	//给有效状态找存储下标 
	if(h[cur][t] == -1){
   	//这个有效状态之前没存过 
		q[cur][++cnt[cur]] = t;	//储存它的下标 cnt更新当前格子的有效状态数 
		h[cur][t] = state;	//储存具体的有效状态 
		v[cur][t] = w;	//储存符合当前有效状态的所有方案数 
	}
	else v[cur][t] += w;	//这个有效状态之前存过，把它的合法方案数累加 
}

int main(){
   
//    ios::sync_with_stdio(false);
//    cin.tie(0), cout.tie(0);
    int n, m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++){
   	//读入n * m的矩阵 
	char a[15];
    	scanf("%s", a + 1);
    	for(int j = 1; j <= m; j++){
   
    		if(a[j] == '.'){
   
    			g[i][j] = 1;	//不是障碍标为1，是障碍标为0 
    			ex = i, ey = j;	//记录最后一个有效格子，我们要在最后一个有效格子记录所有方案 
			}
		}
	}
	memset(h, -1, sizeof(h));	//初始化滚动哈希表（"两个"哈希表的元素值均为-1） 
	int cur = 0;
	insert(cur, 0, 1);	//最初的分界线，对应的方案数为1
	for(int i = 1; i <= n; i++){
   	 //枚举所有行
		for(int j = 1; j <= cnt[cur]; j++){
   	 //更新下一行新的分界线状态，从轮廓线是 一条直线和上方最右边格子的最右边 转换到 一条直线和下方最左边格子的最左边  
			h[cur][q[cur][j]] <<= 2;	//新的一行所有有效状态都整体右移一位（用<<的原因是所有有效状态是从右往左记录的） 
		}
		for(int j = 1; j <= m; j++){
   	//枚举所有格子
			int l = cur;	//保存之前的状态（h[l][q[l][k]]是之前格子转移后的有效状态，v[l][q[l][k]]是之前格子转移后的方案数） 
			cur ^= 1;	//cur ^= 1，更新为当前格子 
			cnt[cur] = 0;	//当前格子转移后的有效状态数量初始化为0 
			memset(h[cur], -1, sizeof(h[cur]));	//清空滚动哈希表中记录当前的有效状态 
			for(int k = 1; k <= cnt[l]; k++){
   	//遍历从上一个格子转移之后得到的所有有效状态 
				int state = h[l][q[l][k]];	//state是具体的有效状态，便于后续对状态中某一特定位上的数进行修改 
				LL w = v[l][q[l][k]];	//w是符合这个有效状态的所有方案数 
				int x = get(state, j - 1), y = get(state, j);	//x和y的具体位置跟之前图示的x和y相同 
				//下面是上面图示的所有情况 
				if(g[i][j] == 0){
   	//第一种情况 
					if(!x && !y){
   
						insert(cur, state, w);
					}
				}
				else if(!x && !y){
   	//第二种情况 
					if(g[i + 1][j] && g[i][j + 1]) insert(cur, state + set(j - 1, 1) + set(j, 2), w);
				}
				else if(!x && y){
   	//第三种情况 
					if(g[i + 1][j]) insert(cur, state + set(j - 1, y) - set(j, y), w);
					if(g[i][j + 1]) insert(cur, state, w);
				}
				else if(x && !y){
   	//第四种情况 
					if(g[i][j + 1]) insert(cur, state + set(j, x) - set(j - 1, x), w);
					if(g[i + 1][j]) insert(cur, state, w);
				}
				else if(x == 1 && y == 1){
   	//第五种情况 
					for(int s = 1, u = j + 1;;u++){
   
						int p = get(state, u);
						if