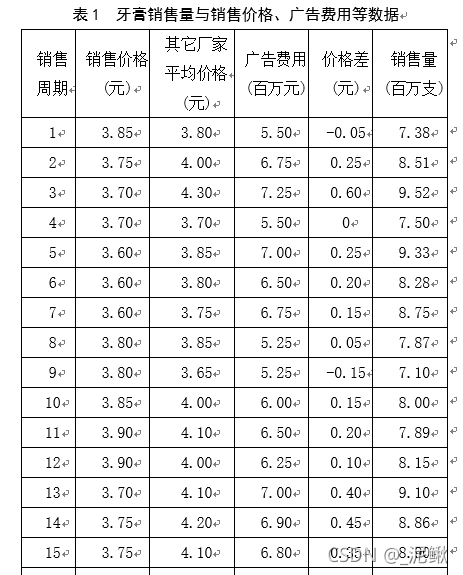
掌握一元线性回归、多元线性回归模型的建模原理、估计及检验方法。 能运用相应的统计软件(SAS\SPSS\R)进行计算、分析。 某大型牙膏制造企业为了更好地拓展产品市场,有效地管理库存,公司董事会要求销售部门根据市场调查,找出公司生产的牙膏销售量与销售价格、广告投入等之间的关系,从而预测出在不同价格和广告费用下的销售量。为此,销售部的研究人员收集了过去30个销售周期(每个销售周期为4周)公司生产的牙膏的销售量、销售价格、投入的广告费用,以及同期其它厂家生产的同类牙膏的市场平均销售价格,见表1(其中价格差指其它厂家平均价格与公司销售价格之差)。 试根据这些数据建立一个数学模型,分析牙膏销售量与其它因素的关系,为制订价格策略和广告投入策略提供数量依据。 对于大多数消费者而言,牙膏作为一种生活的必需品,在购买同类牙膏时,更多的会关心不同品牌之间的价格差,而不是它们的价格本身。 其他厂商平均价格能展现牙膏的市场均价,与自身品牌的价格的差异可能会影响消费者选择。但是,在研究各个因素对销售量的影响时,用价格差代替公司销售价格和其他厂家平均价格,更加直观和合适。 广告费用多少决定了厂家对于牙膏的推广力度,会在一定程度上影响消费者的选择。较大的广告推广力度,会加深消费者对产品的认知并在一定程度上提高产量。 如图所示,设销售量为 ,销售价格、其它厂家平均价格、广告费用和价格差分别作为 ,绘制4个散点图。 此外,如表所示,计算每个自变量与销售的皮尔逊相关系数。 由上述分析与散点图可看出,牙膏销售量与广告费用和价格差呈线性关系,与其它厂家平均价格、广告费用和价格差相关程度较高。 import pandas as pd
import numpy as np
data = pd. read_csv( "E:\Code\Jupyter Notebook Code\数学建模\Data\多元线性回归数据.csv" ) . iloc[ : , 1 : ]
data. head( )
data. corr( method= 'pearson' )
import matplotlib. pyplot as plt
import seaborn as sns
label = data. iloc[ : , - 1 ] . to_numpy( )
factor = data. iloc[ : , : - 1 ] . to_numpy( )
plt. rcParams[ 'font.sans-serif' ] = [ 'SimHei' ]
plt. rcParams[ 'axes.unicode_minus' ] = False
plt. figure( figsize= ( 8 , 8 ) )
plt. subplot( 2 , 2 , 1 )
plt. grid( )
plt. scatter( label, factor[ : , 0 ] )
plt. xlabel( '销售量' , size= 15 )
plt. ylabel( '销售价格' , size= 15 )
plt. subplot( 2 , 2 , 2 )
plt. grid( )
plt. scatter( label, factor[ : , 1 ] )
plt. xlabel( '销售量' , size= 15 )
plt. ylabel( '其它厂家平均价格' , size= 15 )
plt. subplot( 2 , 2 , 3 )
plt. grid( )
plt. scatter( label, factor[ : , 2 ] )
plt. xlabel( '销售量' , size= 15 )
plt. ylabel( '广告费用' , size= 15 )
plt. subplot( 2 , 2 , 4 )
plt. grid( )
plt. scatter( label, factor[ : , 3 ] )
plt. xlabel( '销售量' , size= 15 )
plt. ylabel( '价格差' , size= 15 )
plt. tight_layout( )
data = read.csv( "E:/Code/R Code/Data/多元线性回归数据.csv" )
cor( data[ 2 : 6 ] , method = "pearson" )
记牙膏销售量为
Y
Y
Y
X
1
X_{1}
X 1
X
2
X_{2}
X 2
X
3
X_{3}
X 3
Y
=
β
0
+
β
1
X
1
+
β
2
X
2
+
β
3
X
3
Y=\beta_{0}+\beta_{1} X_{1}+\beta_{2} X_{2}+\beta_{3} X_{3}
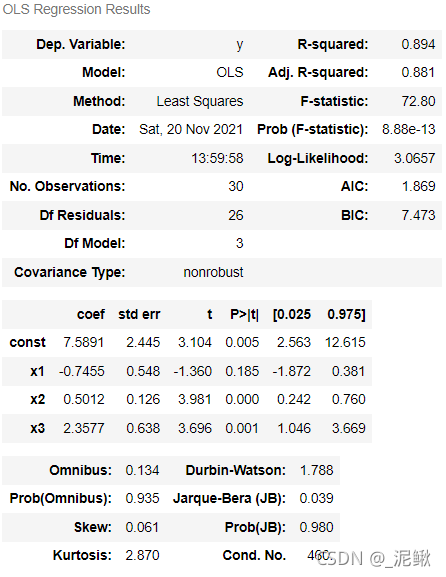
Y = β 0 + β 1 X 1 + β 2 X 2 + β 3 X 3 拟合模型,得到
β
0
=
7.5891
\beta_{0}=7.5891
β 0 = 7 . 5 8 9 1
β
1
=
−
0.7455
\beta_{1}=-0.7455
β 1 = − 0 . 7 4 5 5
β
2
=
0.5012
\beta_{2}=0.5012
β 2 = 0 . 5 0 1 2
β
3
=
2.3577
\beta_{3}=2.3577
β 3 = 2 . 3 5 7 7
Y
=
7.5891
+
−
0.7455
X
1
+
0.5012
X
2
+
2.3577
X
3
Y=7.5891+-0.7455X_{1}+0.5012X_{2}+2.3577X_{3}
Y = 7 . 5 8 9 1 + − 0 . 7 4 5 5 X 1 + 0 . 5 0 1 2 X 2 + 2 . 3 5 7 7 X 3 import statsmodels. api as sm
label = data. iloc[ : , - 1 ] . to_numpy( )
factor = data. iloc[ : , : - 1 ] . to_numpy( )
Y= label
X= factor[ : , 1 : ]
X= sm. add_constant( X)
model = sm. OLS( Y, X) . fit( )
model. summary( )
y_train_pred = model.predict( X)
plt.figure( figsize= ( 8 , 4 ) )
plt.plot( label.reshape( - 1 , 1 ) , color= '#00b0ff' , label= "Observations" , linewidth= 1.5 )
plt.plot( y_train_pred, color= '#ff3d00' , label= "Prediction" , linewidth= 1.5 )
plt.legend( loc= "upper left" )
plt.grid( alpha= 0.6 )
plt.tight_layout( )
test_data = data.frame( data[ 3 ] , data[ 4 ] , data[ 5 ] , data[ 6 ] )
colnames( test_data) <- c( 'X1' , 'X2' , 'X3' , 'Y' )
model_lm = lm( Y~ X1+ X2+ X3, data= test_data)
summary( model_lm)































 374
374

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










