归并排序
-
算法描述
归并排序是 分治思想 的应用,即将原待排数组 递归或迭代地 分为左右两半,直到数组长度为1,然后对左右数组进行合并(merge),在合并中完成排序。详细过程需结合代码理解,如下动图展示了{4,6,2,1,7,9,5,8,3}的归并排序过程(自顶向下非原地)。合并过程采用 非原地 合并方法,即依次比较两部分已排序数组,将比较结果依次写入 新空间 中。后续会介绍一种称作 原地(in-place) 归并排序的改进,使得空间复杂度达到 常数级 (自底向上时,O(1)O(1))。
如下树状图中的橙色线表示递归的轨迹(自顶向下递归归并排序)。
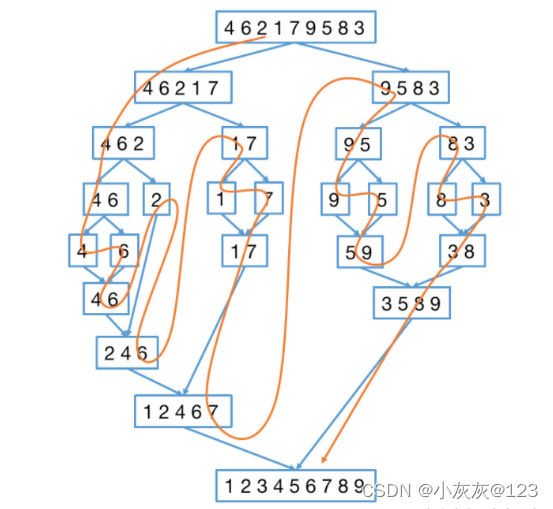
-
稳定性:稳定。
合并时的此判断中的等号if(left[l_next] <= right[r_next]),保证了出现相等元素时,居左的元素总会被放在左侧,稳定性不受影响。
- 自顶向下和自底向上
可以通过 自顶向下(top-down) 或 自底向上(bottom-up) 的方式实现归并排序。
自顶向下(top-down):从输入数组出发,不断二分该数组,直到数组长度为1,再执行合并。适合用 递归 实现。
自底向上(bottom-up):从输入数组的单个元素出发,一一合并,二二合并,四四合并直到数组有序。适合用 迭代 实现。
后续给出 自顶向下原地 / 自顶向下非原地 / 自底向上原地 / 自底向上非原地 四种代码实现。
- 原地归并
前述归并排序,每一次合并都是将两部分待合并数组的比较结果写入一个与arr等大小的临时数组tmpArr中,写入后再将tmpArr中的合并结果写回到arr中。于是tmpArr的空间开销即为该实现的空间复杂度,为 O(n)O(n)。实际上,通过一种 原地旋转交换 的方法(俗称手摇算法/内存反转算法/三重反转算法),则只需要 O(1)O(1) 的辅助空间(由于递归空间为 O(logn)O(logn),其总的空间复杂度仍为 O(logn)O(logn))。以下介绍旋转交换的实现方法。
以b4b5b6a1a2a3序列为例,欲将b4b5b6和a1a2a3交换位置转换为a1a2a3b4b5b6,只需要执行三次旋转即可:
旋转b4b5b6,得到b6b5b4
旋转a1a2a3,得到a3a2a1
旋转b6b5b4a3a2a1得到a1a2a3b4b5b6。
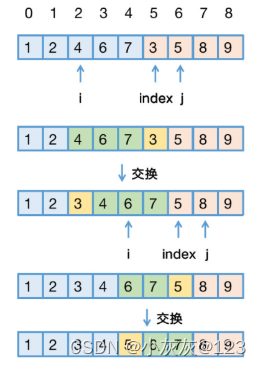
以{1, 2, 4, 6, 7}与{3, 5, 8, 9}的合并为例,观察借助手摇算法实现原地归并的过程。
在{1, 2, 4, 6, 7}中找到第一个大于3的数4,其下标为2,i = 2。index = j = 5。在{3, 5, 8, 9}中找到第一个大于arr[i] = arr[2] = 4的数5,其下标为6,j = 6。
如上操作使得[0, i - 1]必是最小序列,[index, j - 1]必小于arr[i]。因此交换[i, index - 1]和[index, j - 1](采用三次旋转完成交换)能够使得原右边数组中某一段序列插入到左边数组中,使得这部分序列在整个数组中有序。
交换后,继续执行上述过程,直到不满足该条件 :i < j && j <= rightEnd。
- 复杂度分析
自顶向下非原地 - 时间复杂度
每次减半后的左右两半对应元素的对比(if(left[l_next] <= right[r_next]))和赋值(resArr[res_next++] = ??? )总是必须的,也即在每一层递归中(这里的一层指的是 递归树 中的层),比较和赋值的时间复杂度都是 O(n)O(n),数组规模减半次数为 lognlogn,即递归深度为 lognlogn,也即总共需要 lognlogn 次 O(n)O(n) 的比较和赋值,时间复杂度为 O(nlogn)O(nlogn)。
也可以这样求解。当 n=1 时,排序只需常数时间,可以记为 1。n个元素的归并排序时间由 n/2 个元素的归并排序的两倍,再加上将两个n/2大小的已排序数比较及合并的耗时得到。得到如下两个式子(第2个式子加号右边的 n 表示比较及合并的时间)。

- 空间复杂度
递归深度为 lognlogn,递归过程中需要一个长度为 n 的临时数组保存中间结果,空间复杂度为 O(n)O(n)。
- 自顶向下原地
时间复杂度
该方式的时间复杂度计算参考了此篇文章。
当序列为 链表 时,手摇算法只需做如下指针调整即可(只做示意,非实际代码)。
双向链表时:
tmp = index.prev
index.prev = i.prev
i.prev = j.prev
j.prev = tmp
单向链表时:
(i-1).next = index
(index-1).next = j
(j-1).next = i
对于长度为 n 的序列,手摇算法操作元素个数至多不超过 n/2 个,容易得到下述递推式。
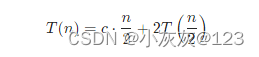
-
由前述计算方法可复杂度为 O(nlogn)O(nlogn) 。
-
当序列为数组时,以 {1,3,5,7,…k} 和 {2,4,6,8,…,n} 的手摇合并为例,对于长度为 n 的序列,一次手摇算法需要对一半规模(非严格的一半)的元素进行翻转(翻转两次)。例如第一次手摇,需翻转{3, …, k}和{2}( {2} 只有一个元素,实际不翻转)得到 {k, …, 3} 和 {2} ,然后再翻转 {k, …, 3, 2} 得到 {2, 3, …, k}。下一次手摇对象是{5, …, k}和{4},翻转元素个数相比上一次减少一个,可知完成 {1,3,5,7,…k} 和 {2,4,6,8,…,n} 的手摇合并所需要的对元素的翻转次数是 c*n^2c∗n 2 (等差数列求和,c是一常数),于是有下列递推式。

-
上述复杂度为 最坏及平均情形, 最好情形是输入数组已排序,则无需手摇,但序列长度为 n 时需要的比较判断次数是 n,于是最好情形的递推式如下,复杂度为 O(nlogn)O(nlogn)。
-
空间复杂度
递归深度为 lognlogn,手摇算法仅需 O(1)O(1) 的辅助空间,综合来看空间复杂度为 O(logn)O(logn)。
- 自底向上非原地 & 自底向上原地
时间复杂度
同自顶向下非原地/原地的分析类似,只是程序运行过程从递归变为了迭代。
- 空间复杂度
自底向上非原地归并:迭代过程中需要一个长度为 n 的临时数组保存中间结果,空间复杂度为 O(n)O(n)。
自底向上原地归并:手摇算法仅需 O(1)O(1) 的辅助空间,其他空间开销均为常数级,空间复杂度为 O(1)O(1)。
- 总结
四种归并排序的时空复杂度总结如下(待排序序列是数组形式,不考虑链表形式)。
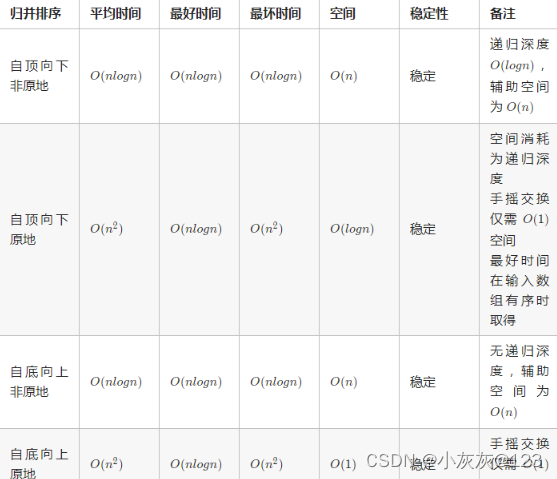
根据上述分析,原地相比非原地,空间消耗较少,采用自底向上原地归并排序时空间复杂度为常数级 O(1O(1),但需要 O(n^2)O(n 2 ) 的时间复杂度。是一种以时间换空间的做法,通常空间不为瓶颈时,应采用 效率更高的非原地归并排序。
代码 - 自顶向下非原地归并
public int[] mergeSort(int[] arr) {
if (arr.length < 2) return arr;
int[] tmpArr = new int[arr.length];
mergeSort(arr, tmpArr, 0, arr.length - 1);
return arr;
}
private void mergeSort(int[] arr, int[] tmpArr, int left, int right) {
if(left < right) {
int center = left + (right - left) / 2;
mergeSort(arr, tmpArr, left, center);
mergeSort(arr, tmpArr, center + 1, right);
merge(arr, tmpArr, left, center, right);
}
}
// 非原地合并方法
private void merge(int[] arr, int[] tmpArr, int leftPos, int leftEnd, int rightEnd) {
int rightPos = leftEnd + 1;
int startIdx = leftPos;
int tmpPos = leftPos;
while (leftPos <= leftEnd && rightPos <= rightEnd) {
if (arr[leftPos] <= arr[rightPos]) {
tmpArr[tmpPos++] = arr[leftPos++];
}
else {
tmpArr[tmpPos++] = arr[rightPos++];
}
}
// 比较完成后若左数组还有剩余,则将其添加到tmpArr剩余空间
while (leftPos <= leftEnd) {
tmpArr[tmpPos++] = arr[leftPos++];
}
// 比较完成后若右数组还有剩余,则将其添加到tmpArr剩余空间
while (rightPos <= rightEnd) {
tmpArr[tmpPos++] = arr[rightPos++];
}
// 容易遗漏的步骤,将tmpArr拷回arr中
// 从小区间排序到大区间排序,大区间包含原来的小区间,需要从arr再对应比较排序到tmpArr中,
// 所以arr也需要动态更新为排序状态,即随时将tmpArr拷回到arr中
for(int i = startIdx; i <= rightEnd; i++) {
arr[i] = tmpArr[i];
}
}
- 自顶向下原地归并
public int[] mergeSort(int[] arr) {
if (arr.length < 2) return arr;
mergeSort(arr, 0, arr.length - 1);
return arr;
}
private void mergeSort(int[] arr, int left, int right) {
if(left < right) {
int center = (left + right) / 2;
mergeSort(arr, left, center);
mergeSort(arr, center + 1, right);
merge(arr, left, center, right);
}
}
/**
* 原地排序的合并方法
* #1. 对左右两部分已排序数组,记左数组第一个数下标为i,记右数组第一个数下标为j
* #2. 找到左数组中第一个大于右数组第一个数字的数,记其下标为i
* #3. 以index暂存右数组第一个元素的下标index = j,
* #4. 找到右数组中第一个大于arr[i]的数,记其下标为j
* #5. 交换[i, index-1]和[index, j]数字,通过三次翻转实现,翻转[i, index-1],翻转[index, j],翻转[i, j]
* 重复上述过程直到不满足(i < j && j <= rightEnd)
*/
private void merge(int[] arr, int leftPos, int leftEnd, int rightEnd) {
int i = leftPos, j = leftEnd + 1; // #1
while(i < j && j <= rightEnd) {
while(i < j && arr[i] <= arr[j]) i++; // #2
int index = j; // #3
while(j <= rightEnd && arr[j] < arr[i]) j++; // #4
exchange(arr, i, index - 1, j - 1); // #5
}
}
// 三次翻转实现交换
private void exchange(int[] arr, int left, int leftEnd, int rightEnd) {
reverse(arr, left, leftEnd);
reverse(arr, leftEnd + 1, rightEnd);
reverse(arr, left, rightEnd);
}
private void reverse(int[] arr, int start, int end) {
while(start < end) {
swap(arr, start, end);
start++;
end--;
}
}
- 自底向上非原地归并
public int[] mergeSortBU(int[] arr) {
if (arr.length < 2) return arr;
int[] tmpArr = new int[arr.length];
// 间隔,注意不能写成gap < arr.length / 2 + 1,此种写法只适用于元素个数为2的n次幂时
for(int gap = 1; gap < arr.length; gap *= 2) {
// 基本分区合并(随着间隔的成倍增长,一一合并,二二合并,四四合并...)
for(int left = 0; left < arr.length - gap; left += 2 * gap) {
// 调用非原地合并方法。leftEnd = left+gap-1; rightEnd = left+2*gap-1;
merge(arr, tmpArr, left, left + gap - 1, Math.min(left + 2 * gap - 1, arr.length - 1));
}
}
return arr;
}
- 自底向上原地归并
public int[] mergeSortBUInPlace(int[] arr) {
if (arr.length < 2) return arr;
// 间隔,注意不能写成gap < arr.length / 2 + 1,此种写法只适用于元素个数为2的n次幂时
for(int gap = 1; gap < arr.length; gap *= 2) {
// 基本分区合并(随着间隔的成倍增长,一一合并,二二合并,四四合并...)
for(int left = 0; left < arr.length - gap; left += 2 * gap) {
// 调用原地合并方法。leftEnd = left+gap-1; rightEnd = left+2*gap-1;
merge(arr, left, left + gap - 1, Math.min(left + 2 * gap - 1, arr.length - 1));
}
}
return arr;
}






















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








