微观量子体系的运动方程
在量子力学中,我们建立了描述微观量子体系的运动方程:Schrödinger
方程,其给出了体系微观态随时间演化的动力学描述,即
其中  为体系在
t
时刻的微观态、
为体系在
t
时刻的微观态、
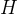 为体系的
Hamilton
量。而体系的一个微观态可以由能量本征态
为体系的
Hamilton
量。而体系的一个微观态可以由能量本征态  的线性组合给出,能量本征态满足方程
的线性组合给出,能量本征态满足方程
这里给出了本征态 |
ν
〉
对应的本征值
E
ν
.
根据本征态的正交归一和完备性,一个量子态可以表示为
在  的情况下,描述体系的方程可以由经典的
Hamilton
正则方程给出,即
的情况下,描述体系的方程可以由经典的
Hamilton
正则方程给出,即
这里 r
和
p
分别为体系的正则坐标和正则动量。但无论是经典的
Hamilton
方程还是量子的
Schrödinger
方程,其都给出了体系微观态的完全描述,但对于一个自由度为 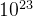 量级的宏观体系,真正重要的宏观性质的个数却很少,因此建立一种能从众多自由度中提取出重要信息的方法是关键的。而统计力学就是这样的一种方法,其建立了一条从微观到宏观的道路,着手处理宏观系统的宏观可观测性质。这里我们所说的宏观可观测性质包括:粒子数 N
,内能
E
,体积
V
,压强
p
,温度
T
,熵
S
,化学势
µ
等。
量级的宏观体系,真正重要的宏观性质的个数却很少,因此建立一种能从众多自由度中提取出重要信息的方法是关键的。而统计力学就是这样的一种方法,其建立了一条从微观到宏观的道路,着手处理宏观系统的宏观可观测性质。这里我们所说的宏观可观测性质包括:粒子数 N
,内能
E
,体积
V
,压强
p
,温度
T
,熵
S
,化学势
µ
等。
在本讲义(參考)中,我们主要处理的是热力学平衡态的性质,这里的平衡态指的是宏观性质确
定、不随时间演化的宏观状态。且我们主要处理的是单组分子的性质
系综理论
系综和遍历性假设
当宏观系统处于热力学平衡态时,所有满足约束条件的可能微观态的集合称为系综
。系综的目的是为了研究宏观系统的宏观性质的一种数学处理手段,其为一种方法论,系综的选择不影响物理实在。一个力学量在系综的框架下给出的统计平均称为系综平均,其给出宏观物理量的性质(值得注意的一点:在概率论中,基本公理基于三元组
 ,即样本空间
,即样本空间
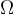 、
、
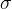 代数
代数
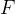 以及概率
以及概率
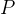 ,而这里的样本空间
,而这里的样本空间
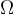 和系综有着类似的意义,其都给基于代数规则给出概率)。在量子力学中,微观态的集合为满足约束条件下的
Hilbert
空间中的可能态;
在经典力学下即为相空间中由 (
p
,
r
)
定义的轨迹。
和系综有着类似的意义,其都给基于代数规则给出概率)。在量子力学中,微观态的集合为满足约束条件下的
Hilbert
空间中的可能态;
在经典力学下即为相空间中由 (
p
,
r
)
定义的轨迹。
为了给出系统的宏观性质,除了基于系综的基本概念以及假设,我们还需要用到宏观系
统的热力学性质。根据热力学基本定律,我们有
对于表面的情况,还需要引入表面张力的贡献。根据
Euler
齐函数定理,我们得到
通过
Legendre
变换,我们可以定义其他的热力学函数并给出微分关系,他们包括
焓
Helmholtz
自由能
以及
Gibbs 自由能
引入统计力学第一个基本假设:遍历性假设。
其表述如下:在宏观的测量时间内,宏观系统已经以一定概率遍历所有允许的微观状态,所测量的宏观物理量是历经微观态的统计平均。
遍历性假设给出的重要信息为:在宏观测量时间下,时间平均等于系综平均,即对于某个物理量
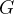 有
有
系综理论给出微观态与宏观态性质之间联系的基础,而一个真正联系宏观量与微观量的公式为
Boltzmann
的熵公式,即
这里  为
Boltzmann 常数(在不引起歧义的情况下,有时忽略下标
为
Boltzmann 常数(在不引起歧义的情况下,有时忽略下标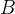 )
,
)
,
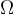 为微观状态数。
为微观状态数。
微正则系综与等概率原理
统计力学中,除了遍历性假设,另一个重要的基本假设为等概率原理,其表述为:对于一个固定能量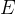 、粒子数
、粒子数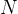 和
和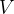 的热力学宏观平衡系统,其达到每个微观态的概率是相同的。这里的系统被称为微正则系综,其微观状态数为
的热力学宏观平衡系统,其达到每个微观态的概率是相同的。这里的系统被称为微正则系综,其微观状态数为
这里  表示微观态的集合。但实际上,一个系统的能量实际上并不是完全固定的,其实际 上处于区间
表示微观态的集合。但实际上,一个系统的能量实际上并不是完全固定的,其实际 上处于区间  中。在以上的框架下,微正则系综中一个微观态出现的概率为
中。在以上的框架下,微正则系综中一个微观态出现的概率为
这里需要条件能量 根据
Boltzmann
公式,有
根据
Boltzmann
公式,有
因此结合热力学基本公式我们有
这里定义了

接下来我们用理想气体的例子来说明。定义能量处于 (0
, E
)
的总的微观状态数为
Φ(
E
)
,
因此我们有
量子力学中,理想气体可以认为有
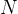 个处于势
个处于势
的粒子。量子力学给出
和能量
且微观态集合由
由
Schrödinger
方程给出,且  。因此有
。因此有
这里由于宏观系统的能量量级远远大于微观态分割,因此可以把求和转化为积分。根据 维
维
球的体积公式
其中 Γ(
x
)
定义为
故我们可以计算上述积分为
其中 来自于粒子的全同性。这里我们利用了以下事实:微观粒子态的个数远远大于微观粒子数,因此相同微观粒子占据同一微观态的概率远远小于 1 且
来自于粒子的全同性。这里我们利用了以下事实:微观粒子态的个数远远大于微观粒子数,因此相同微观粒子占据同一微观态的概率远远小于 1 且 .
故能量在
.
故能量在  的微观态数目为
的微观态数目为
容易验证, 大致量级为
大致量级为  .
故
.
故
这里
f
(
V
)
是某个和
V
有关的函数。故根据之前的公式,我们有
微正则系综给出了孤立体统的统计方法,但由于能量固定的系统并不方便研究,故下节中将引入正则系综。
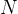 维球体积(拓展)
维球体积(拓展)
在此之前,我们先给出
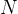 维球体积的证明。记
维球体积的证明。记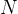 维球体积为
维球体积为 ,其正比于
,其正比于 ,设
,设
则表面积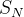 满足
满足
考虑积分
并且有
故得证。
參考:
苏禹<<统计力学>>
(此讲义为本人于
2021
年春季参加中国科学技术大学化学与材料科学学院《统计力学》课
程整理的课程笔记,仅供参考)
普通物理学网络课程(第五章、第六章、第十二章、第十三章、第十四章)























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








