信息量 香农熵 交叉熵 KL散度

信息量：

信息量（I）对事件x，其发生概率为p(x),则其对应的信息量I(x)为：

事件信息量与事件发生概率成反比 

例如：假定晴天为事件h，阴天为事件t，我猜测明天晴天的概率为0.2，阴天的概率为0.8。

则对于我猜测的情况而言，其所包含的信息量为：

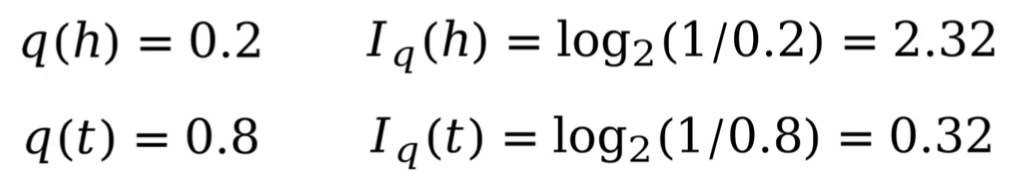
因此：小概率事件信息量大，大概率事件信息量小。

香农熵

香农熵描述了一个概率分布蕴含的平均信息量，定义如下：

其中，:第i个事件的概率，：第i个事件的信息量。

熵：表示了概率分布的平均信息量

例如：假定晴天h，阴天t 的概率分布为0.2，0.8。

则对于我猜测的情况而言，其香农熵为：

交叉熵

交叉熵（H）：预测概率分布对真实概率分布的估计，这个估计值就是交叉熵。

假定预测概率分布为p，真是概率分布为q，则：

即：真实概率分布与预测概率分布信息量的累加和 

例如：假定晴天h，阴天t 的预测概率分布q为0.2，0.8，但是晴天h，阴天t 的真实概率分布p为0.5，0.5.则预测概率分布q与真实概率分布p的交叉熵为：

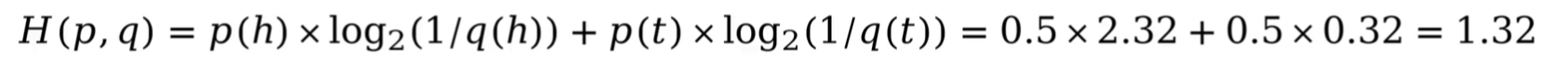
KL散度 

KL散度（D）：量化分析两个概率分布的区别。

 即：真实概率分布与预测概率分布的交叉熵 - 真实概率分布的香农熵

KL散度的性质：

 

仅当p q概率分布完全相同时，等号成立

不可交换（公式定义可知） 

qθ表示基于参数θ预测的概率分布，最小化KL散度等同于深度学习领域的 最小化交叉熵损失，因为真实概率分布的香农熵，不存在参数θ，其梯度为0 。