数论专题总结

最新推荐文章于 2024-03-31 16:30:28 发布

原创最新推荐文章于 2024-03-31 16:30:28 发布 · 257 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#数论 #ACM #算法

acwing-869-试除法求约数

题意

给你n个正整数ai,对于每个整数ai，将每个数分解质因数，并按照质因数从小到大的顺序输出每个质因数的底数和指数。

输入
第一行包含整数n,
接下来n行，每行包含一个整数ai。

输出
对于每个正整数ai,从小到大的输出其分解质因数后，每个质因数的底数和指数，每个底数和指数占一行。

数据范围1<n<100;
2<=ai<=2*10e9;

输入样例

2
6
8

输出样例

2 1
3 1
2 3

解题思路

我们可以用试除法来解决，i从2开始试除，如果说可以被我的x整除，那么i一定就是质数，为什么呢？因为枚举到i时，i之前的所有的质因子都已经除完了，因此，i中不可能还含有i之前的质因子，因此i就一定是n的一个质因子。于是我们通过枚举试除就可以求出n所有的质因子咯。

如何优化

我们刚才的思路是让i从2开始一直枚举到n，因此时间复杂度为O(n)的，但是我们知道任意的一个数一定有且仅有一个大于 $n\sqrt{n}$ 的质因子，同样的，当我们除到 $n\sqrt{n}$ 的时候， $n\sqrt{n}$ 之前的质因子已经除完了，这个时候小于或等于 $n\sqrt{n}$ 且与它最近的一个数也被除掉了，最后剩下来的一定是一个且只有这一个大于 $n\sqrt{n}$ 的质因子。换句话说，如果它有两个的话，因为它之前的n的质因子都已经被出掉了，那么一定是另外一个与它本身相等或者比它还大的数与它相乘等于n，而两个大于 $n\sqrt{n}$ 的数相乘一定是大于n的，因此：有以下结论：

任何一个数最多只有一个大于 $n\sqrt{n}$ 的质因子。当n为完全平方数时，没有大于 $n\sqrt{n}$ 的质因子。

于是我们可以只循环到 $n\sqrt{n}$ ，时间复杂度缩小为O( $n\sqrt{n}$ )。

代码

#include<iostream>
#include<algorithm>
using namespace std;
void divide(int n){
	for(int i = 2; i <= n; i++)
		if(n % i == 0){
			int s = 0;
			while(n % i == 0){
				n /= i;
				s++;
			}
			printf("%d %d\n", i, s);
		}
}
int main(){
    int n; scanf("%d", &n);
    while(n--){
        int x;
        scanf("%d", &x);
        divide(x);
    }
    return 0;
}

868、筛质数

题意：

给你一个正整数n，请你求出1~n中质数的个数。

输入格式
一个整数n
输出格式
一个整数，便是1~n中的质数个数。
数据范围
1<=n<=1e6

输如样例
8
输出样例
4

解题思路

开始我们想到用st数组来标记已经筛过的质数以及它的所有倍数，然后如果枚举到了i，而i还没有被标记，那么说明i一定是质数，因为i之前的所有的因子的倍数都已经做好标记了，如果i是合数的话，那么i一定是它之前的一个数的倍数，即i一定会被筛掉，但是i没有，因此，i一定是质数，然后我们把它加到质数表里面，用cnt来表示当前质数表里面有多少质数。然后我们继续将i的倍数筛掉(这里不管i是否为质数都将它的倍数筛掉），即将其标记为true，此时复杂度为O(nlogn)。

优化

但是我们在纸上画一画就知道，其实很多数都被筛掉了不止一次，因此我们做了很多无用功，于是我们根据算数基本定理，即一个数一定可以表示为很多个质数的多次方相乘，因此，我们只需要筛掉质数就行咯，于是我们就将第二个for循环移到了if里面，这样我们程序的时间复杂度就瞬间降到了O(nlognlogn)，接近O(n)级别。

AC代码（埃氏筛法）

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1e6 + 5;
int primes[N], cnt;
bool st[N];
void divide(int n){
	for(int i = 2; i <= n; i++)
		if(n % i == 0){
			int s = 0;
			while(n % i == 0){
				n /= i;
				s++;
			}
			printf("%d %d\n", i, s);
		}
}
void get_primes(int n){
    for(int i = 2; i <= n; i++){
        if(!st[i]){
            primes[cnt++] = i;
            for(int j = i + i ; j <= n; j += i)
                st[j] = true;
        }
        
    }
}
int main(){
    int n; cin >> n;
    get_primes(n);
    cout << cnt << endl;
    return 0;
}

线性筛法

思路：将每一个合数用它的质因子筛掉即可。
n只会被最小质因子筛掉。
一：当i % primes[j] == 0时，primes[j]一定是i的最小质因子，primes[j]也一定是primes[j]*i的最小质因子。
二：当i % primes[j] != 0时，说明所有的primes[j]前面的数和primes[j]都不能将i整除，因此，primes[j]一定小于i的最小的质因子，也就是小于i的所有质因子，因此，primes[j]也一定是primes[j]*i的最小质因子。
三、对于一个合数x,假设primes[j]是x的最小质因子，由于i在枚举到x之前，一定会枚举到x/primes[j]，当i枚举到x/primes[j]时，x一定会被筛掉，所以，任何一个合数一定会被筛掉，而且我们筛的时候只用最小质因子来筛，而每个合数只有一个最小质因子，因此，每个数只会被筛一次，因此它是线性的。

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1e6 + 5;
int primes[N], cnt;
bool st[N];
void divide(int n){
	for(int i = 2; i <= n; i++)
		if(n % i == 0){
			int s = 0;
			while(n % i == 0){
				n /= i;
				s++;
			}
			printf("%d %d\n", i, s);
		}
}
//埃氏筛法
void get_primes(int n){
    for(int i = 2; i <= n; i++){
        if(!st[i]){
            primes[cnt++] = i;
            for(int j = i + i ; j <= n; j += i)
                st[j] = true;
        }

    }
}
//线性筛法
void get_prime(int n){
    for(int i = 2; i <= n; i++){
        if(!st[i]) primes[cnt ++ ] = i;
        for(int j = 0; primes[j] <= n / i; j++){
            st[primes[j]*i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}
int main(){
    int n; cin >> n;
    get_prime(n);
    cout << cnt << endl;
    return 0;
}

线性筛法在n=1e7时，会比埃氏筛法快一倍！因此，实际比赛时，我们一般是用线性筛法。

五大问题：
试除法为什么可以枚举到 $n\sqrt{n}$ ?
分解质数那道题为什么时间复杂度为O(Ologn)，但是为什么实际分解时却很快呢？
朴素筛法时间复杂度为什么是O(nlogn)?
埃氏筛法是什么原理？
线性筛法为什么是线性的？

约数

1、试除法求所有约数：
若d | n, 则必有 n/d | n，即一个数的约数一定是成对出现的。因此我们只需要枚举较小的那个约数即可，较大的那个约数我们可以之间用n/d算，即我们只需要枚举到d<=n/d即可，即d <= $n\sqrt{n}$

acwing 869

题意

给你n个整数ai,对于每个整数ai,请你按照从小到大的顺序输出他的所有约数。

输入：
2
6
5
输出
1 2 3 6
1 2 4 8

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1e6 + 5;
int primes[N], cnt;
bool st[N];
void divide(int n){
	for(int i = 2; i <= n; i++)
		if(n % i == 0){
			int s = 0;
			while(n % i == 0){
				n /= i;
				s++;
			}
			printf("%d %d\n", i, s);
		}
}
//
void get_primes(int n){
    for(int i = 2; i <= n; i++){
        if(!st[i]){
            primes[cnt++] = i;
            for(int j = i + i ; j <= n; j += i)
                st[j] = true;
        }

    }
}

void get_prime(int n){
    for(int i = 2; i <= n; i++){
        if(!st[i]) primes[cnt ++ ] = i;
        for(int j = 0; primes[j] <= n; j++){
            st[primes[j]*i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}

vector<int> get_divisors(int n){
    vector<int> res;
    for(int i = 1; i <= n / i; i++){
        if(n % i == 0)
            res.push_back(i);
        if(n / i != i) res.push_back(n/i);
    }
    sort(res.begin(), res.end());
    return res;
}
int main(){
    int n;
    cin >> n;
    while(n--){
        int x;
        cin >> x;
        auto res = get_divisors(x);
        for(auto t: res) cout << t << ' ';
        cout << endl;
    }
    return 0;
}

知识点
约数：
（1）试除法求一个数的所有约数，得到：x = p1^a1p2^a2p3^a3…pk^ak
（2）约数个数：(a₁ + 1) * (a₂ + 1) * (a₃ + 1)…(a_k + 1)
（3）约数之和：(p1⁰ + p1¹+ … + p1^a1)… (pk⁰+pk ¹+…+pk^ak);

acwing 870 约数个数

题意：

给你n个正整数ai, 请你输出这些数的乘积的约数个数，答案对1e9+7取模。

输入：一个整数n, 1< n <= 100;
输出：一个整数1 <= ai<= 2*1e9;

输入样例：
3
2
6
8
输出样例：
12

解题思路

这题可以定义一个hash表，用来存储分解出来的每一个质数的指数，分解质因子就是上面的方法，要注意的就是我们枚举完 $n\sqrt{n}$ 以内的所有数之后，还要记得检查一下我们最后的那个x是不是被除到1了，如果没有的话那么说明一定存在唯一一个大于 $n\sqrt{n}$ 的质因子，也是那个最大的质因子。最后我们直接利用我们刚才得出来的约数求和公式求解即可！

AC代码：

#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
#include<unordered_map>
#include <map>
#include <vector>
#include <cstring>
#include <stdio.h>
#include <set>
using namespace std;
#define ll long long
#define endl "\n"
const int maxn=1e5+10;
const ll mod=1e9+7;
int num=0;
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int t;
    cin>>t;
    unordered_map<int, int> primes;//指数
    while (t--)
    {
        int x; cin >> x;
        for(int i = 2; i <= x / i; i++)
        while(x % i == 0){
            x /= i;
            primes[i]++;
        }
        if(x > 1) primes[x]++;//最后一个比根号x更大的质数
    }
    ll res = 1;
    for(auto prime : primes)
        res = res * (prime.second + 1) % mod;
    cout << res << endl;
    return 0;
}

acwing 871 约数之和

题意

给你n个正整数ai, 请你输出这些数的乘积的约数之和，答案对1e9+7取模。

输入：一个整数n, 1< n <= 100;
输出：一个整数1 <= ai<= 2*1e9;

输入样例：
3
2
6
8
输出样例：
12

思路：

其实我们可以很容易发现，求约数个数和求约数之和的公式都需要先将给定的数x进行质数分解，将每个质数的指数保存到对应的hash表中，然后在最后面答案的形式也是相同的，都是分解的质数总数个括号相乘，因此，我们只需要改最后的求和方式即可，于是问题瞬间转化为了求1 + p¹ + p² + p³ + … + p^ai，其实我们很容易发现，它就等价于（(p^ai-1+p^a2-1 + … + p) * p+ 1) + 1 = …(((((((p+1)p + 1)p + 1)p + 1)…)+1)+1)+1，这是一个递归的过程，我们只需要循环求解即可，而我们反推一下：t = t *p +1 → ^t=1 t = p + 1 → ^t=t*p+1 t = p² + p¹ + p⁰ → ^t=t*p+1 →t = p³ + p² + p¹ + p⁰…我们找下规律，t = p+1代入执行一次，则p的最高次数为1，执行2次，则p的最高次数为2，…，而我们要求的最高次数为ai，因此我只需要执行ai次即可。

AC代码

#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
#include<unordered_map>
#include <map>
#include <vector>
#include <cstring>
#include <stdio.h>
#include <set>
using namespace std;
#define ll long long
#define endl "\n"
const int maxn=1e5+10;
const ll mod=1e9+7;
int num=0;
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int t;
    cin>>t;
    unordered_map<int, int> primes;//指数
    while (t--)
    {
        int x; cin >> x;
        for(int i = 2; i <= x / i; i++)
        while(x % i == 0){
            x /= i;
            primes[i]++;
        }
        if(x > 1) primes[x]++;//最后一个比根号x更大的质数
    }
    ll res = 1;
    for(auto prime : primes){
        int p = prime.first, a = prime.second;
        ll t = 1;
        while(a--) t = ((t * p) + 1) % mod;
        res = res * t % mod;
    }

    cout << res << endl;
    return 0;
}

欧拉函数

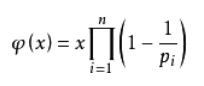
求任意数的欧拉函数模板：（时间复杂度为O(n $n\sqrt{n}$ )

#include <iostream>
#include <algorithm>
#include <queue>
#include <stack>
#include<unordered_map>
#include <map>
#include <vector>
#include <cstring>
#include <stdio.h>
#include <set>
using namespace std;
#define ll long long
#define endl "\n"
const int maxn=1e5+10;
const ll mod=1e9+7;
int num=0;
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int n; cin >> n;
    while(n--){
        int a;
        cin >> a;
        int res = a;
        for(int i = 2; i <= a / i; i++)
            if(a % i == 0){
                res = res / i * (i - 1);
                while(a % i == 0) a /= i;
            }

        if(a > 1) res = res / a * (a - 1); //最后一个大的质因子

        cout << res << endl;
    }
    return 0;
}

![在这里插入图片描述](https://img-blog.csdnimg.cn/20210318231028157.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80Njc1NDIzOQ==,size_16,color_FFFFFF,t_70

线性筛法求欧拉函数（O(n))

题目引入：
给你一个正整数，求1~n中每个数的欧拉函数之和（1 <= n <= 1e6)
输入
6
输出
12

首先，我们引入之前讲过的线性筛模板：

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1e6 + 5;
int primes[N], cnt;
bool st[N];

//埃氏筛法
void get_primes(int n){
    for(int i = 2; i <= n; i++){
        if(!st[i]){
            primes[cnt++] = i;
            for(int j = i + i ; j <= n; j += i)
                st[j] = true;
        }

    }
}
//线性筛法
void get_prime(int n){
    for(int i = 2; i <= n; i++){
        if(!st[i]) primes[cnt ++ ] = i;
        for(int j = 0; primes[j] <= n / i; j++){
            st[primes[j]*i] = true;
            if(i % primes[j] == 0) break;
        }
    }
}
int main(){
    int n; cin >> n;
    get_prime(n);
    cout << cnt << endl;
    return 0;
}

之前已经证明过它的时间复杂度为O(n)了，现在我们只需要在这个模板中插入求欧拉函数的一些代码即可。

首先，我们知道，任何一个质数p的欧拉函数为p - 1，而我们在代码中，当st[i]为假时，即i没有被筛掉时，说明i是一个质数，于是在if(!st[i])条件中插入phi[i] = i - 1;
其次，在循环求解每一个质数时，当满足if(i % primes[j] == 0)时，说明primes[j]是i的一个质因子，我们再分析一下欧拉函数的形式φ(n)=n*(1-1/p₁)(1-1/p₂)(1-1/p₃)(1-1/p₄)……(1-1/p_k)，因此，φ(primes[j] * i) = primes[j] * i * (1-1/p₁)(1-1/p₂)(1-1/p₃)(1-1/p₄)……(1-1/p_k) = primes[j] * φ(i)，因此，我们在条件if(i % primes[j] == 0)中插入求解欧拉函数的代码：phi[i * primes[j]] = primes[j] * phi[i]。
最后，我们还需要想一下，如果不满足if(i % primes[j] == 0)，那么我们该怎么求解欧拉函数，还是和上面的分析一样，如果不满足该条件，说明primes[j]比i的最小质因子还要小，而且primes[j]一定是prime[j] * i的一个质因子，于是我们可以得到φ(primes[j] * i) = primes[j] * i * (1-1/p₁)(1-1/p₂)(1-1/p₃)*(1-1/p₄)……(1-1/p_k) *（1-1/p_j) = （primes[j] - 1）*φ(i)，于是，我们在条件if(i % primes[j] == 0)括号之外在加上求欧拉函数的代码：phi[i * primes[j]] =（ primes[j] - 1 ） * phi[i]。

AC代码：

#include <iostream>
#include <algorithm>
using namespace std;
#define ll long long
#define endl "\n"
const int N =1e5+10;
const ll mod=1e9+7;
int primes[N], cnt = 0;
int phi[N];
bool st[N];

ll euler(int n){
    phi[1] = 1;//根据定义，1的欧拉函数为1，下面我们求2~n的所有的欧拉函数
    for(int i = 2; i <= n; i++){
        if(!st[i]){
            primes[cnt++] = i;
            phi[i] = i - 1;
        }
        for(int j = 0; primes[j] <= n / i; j++){
            st[primes[j] * i] = true;
            if(i % primes[j] == 0){
                phi[primes[j] * i] = phi[i] * primes[j];
                break;
            }
            phi[primes[j] * i] = phi[i] * ( primes[j] - 1);
        }
    }
    ll res = 0;
    for(int i = 1; i <= n; i++) res += phi[i];
    return res;
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    int n; cin >> n;
    cout << euler(n) << endl;
    return 0;
}