【哈夫曼树】介绍与应用

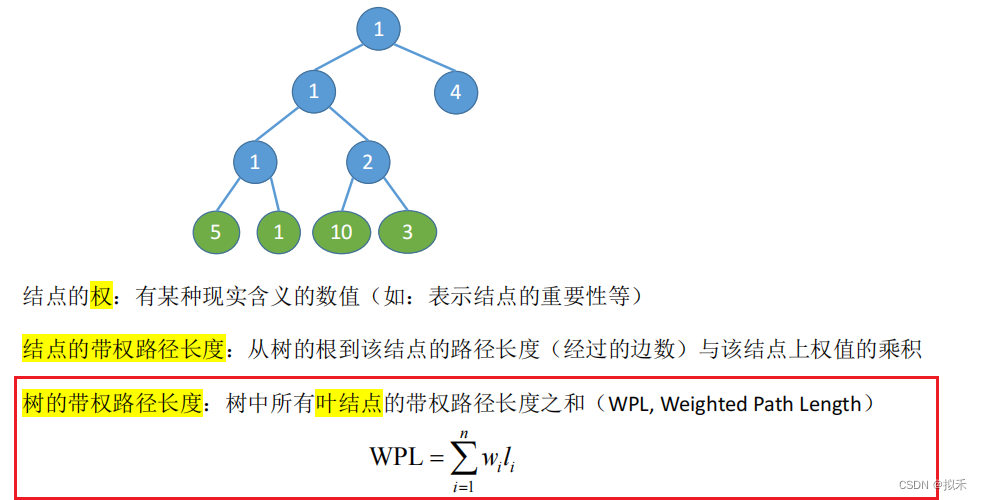
带权路径长度

哈夫曼树（最优二叉树）

在含有n个带权叶结点的二叉树中，其中带权路径长度(WPL)最小的二叉树称为哈夫曼树，也称最优二叉树。

构造哈夫曼树

哈夫曼编码

将字符频次作为字符结点权值，构造哈夫曼树，即可得哈夫曼编码，可用于数据压缩。

固定长度编码――每个字符用相等长度的二进制位表示

可变长度编码――允许对不同字符用不等长的二进制位表示
若没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码，前缀编码解码无歧义，非前缀编码解码有歧义

因哈夫曼树不唯一，因此哈夫曼编码不唯一。