一张纸折叠N次，请从上到下打印所有的：凹凸折痕

一张纸折叠N次，请从上到下打印所有的：凹凸折痕

提示：二叉树中序遍历的经典应用，也是曾经左神见过的Facebook的考试题

---

题目

你亲手拿纸张准备干：

一张纸，折叠1次，你可以看见中间，有一个向下的凹的折痕。

从上到下打印折痕：凹（N=1）

连续折叠2次呢？你可以看见，在第一次凹折痕的上和下，分别新增一个凹折痕与凸折痕。

从上到下打印折痕：凹（2） 凹（1） 凸（2）
连续折叠3次呢？你可以看见，再第二次新增那俩凹凸折痕的各自上下，都会有新增一个凹，一个凸折痕。
自己拿纸张折叠你就知道了

从上到下打印折痕：凹（3） 凹（2）凸（3） 凹（1） 凹（3）凸（2）凸（3）

那么，一张纸折叠N次，请你从上到下打印所有的：凹凸折痕

---

二、解题

其实自己拿纸折叠一比，就知道
第N次折叠，出来的折痕
是在N-1次那俩新出的折痕的上下分别新增凹凸
与1–N-2次折叠的痕迹没关系

这个折痕完全和二叉树对上了【如果把节点x的左子，叫上边折痕，x的右子叫下边折痕】
N=1

N=2

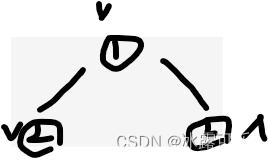
N=3

发下了没，N递增过程中，沿着N-1层的节点，左右各自新增一个凹凸

中序遍历就是折叠痕迹：从上到下打印折痕：凹（3） 凹（2）凸（3） 凹（1） 凹（3）凸（2）凸（3）
咱不用先生成树，直接中序遍历模拟打印：

//N递增过程中，沿着N-1层的节点，左右各自新增一个凹凸
    public static void foldedPaperPrint(int N){
        //递归
        if (N == 0) return;

        System.out.println("N=" + N);
        foldPrint(1, N, true);
        //来到level=1层，最大N层，要打印的flagAo：是凹吗,第一次折叠为凹
    }
    //递归中序遍历打：来到level层，最大N层，要打印的flagAo：是凹还是凸，凹true，凸false
    public static void foldPrint(int level, int N, boolean flagAo){
        if (level > N) return;//多了不行

        //模拟中序遍历打印--左头右
        foldPrint(level + 1, N, true);//左打印凹
        System.out.println(flagAo ? "凹" : "凸");//是打印凹吗？头打印
        foldPrint(level + 1, N, false);//右打印凸
    }
    public static void test2(){
        foldedPaperPrint(0);
        foldedPaperPrint(1);
        System.out.println("---------");
        foldedPaperPrint(2);
        System.out.println("---------");
        foldedPaperPrint(3);
    }


    public static void main(String[] args) {
        test2();
    }

结果自然明了：

N=1
凹
---------
N=2
凹
凹
凸
---------
N=3
凹
凹
凸
凹
凹
凸
凸

---

总结

提示：重要经验：

1）本题打印折叠痕迹，是经典的二叉树的应用，第一次见我就敏感地想到了
2）中序遍历模拟实现打印，不需要提前建树哦！
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。