一排正方形，有红色绿色两种颜色，将左边全变红色，右边全变绿色，最少需要染色的个数是多少

一排正方形，有红色绿色两种颜色，将左边全变红色，右边全变绿色，最少需要染色的个数是多少？

提示：空间换时间，提前准备前缀统计量，在遍历i的过程中，o(1)速度拿到左右G/R的数量，这样就完成优化。

---

题目

一排正方形数组arr，有红色R,绿色G两种颜色，将左边全变红色，右边全变绿色，最少需要染色的方块个数是多少？
目标就是让所有红色方块离左边近，所有绿色方块离右边近。

---

一、审题

示例：
arr=RGRGR
变这样：
arr=RRRGG
至少变2个

可能也有别的方案，放在想办法让左边全是R，右边全是G

---

暴力解，来到i，让0–i，全变R，让i+1–N-1全变G，每次暴力查找统计量，整体o(n^2)复杂度

每次来到i位置，都去数一下0–i上有多少个G：N1个
每次来到i位置，都去数一下i=1–N-1上有多少个R：N2个
这样的话，左边让G变R，右边让R变G，整体至少需要变：N1+N2个
这就是结果
如果每次都暴力索引查找的话，每一个i是N种情况
内部索引查找又是o(n)
整体就是o(n*n)=o(n^2)复杂度，不可取！

数组，范围上统计数量，范围上求累加和等等，完全可以通过提前准备前缀信息搞定，比如：前缀累加和，前缀数量等等
利用空间换时间来加速算法的优化！

本题就这么干！！！

---

左边让G变R，右边让R变G，利用前缀统计量count加速：o(n)复杂度

其实左边R，右边G是没有明确的一个分界线的
我们就枚举分界线，来到i位置
以i为分界线，左边：0–i，G全变R，右边：i+1–N-1的R全变G
看看每一个i，左边有多少G变R，右边有多少R变G？左右变化的和，就是咱们至少要变的数量
整个0–N-1所有分界线都有一个变数，更新给min就是咱们的结果！

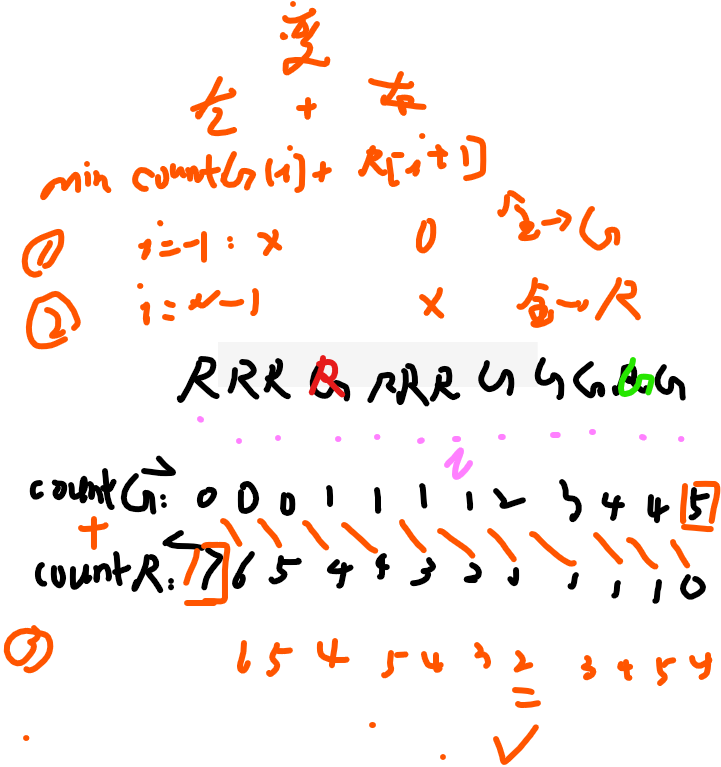
以i为分界线，左边：0–i，G全变R，右边：i+1–N-1的R全变G
（1）countG：从左往右统计G的个数，目的是想让左边的全变R，所以G的个数，就是需要变为R的个数
（2）countR：从右往左统计R的个数，目的是想让右边的全变G，所以R的个数，就是需要变为G的个数
（3）当分界线i=-1时，意味着让所有arr都变为G，所以只看R有多少个？则需要变这么多个方块：countR[i+1]=countR[0]
（4）当分界线i=N-1时，意味着让所有arr都变为R，所以只看G有多少个？则需要变这么多个方块：countG[i]=countR[N-1]
（5）其余i位置，左边让G变R，变这么多个：countG[i]，右边让R变G，变这么多个：countR[i+1]，即两者错位相加，看上图，最终变整体个数：countG[i]+countR[i+1]，每一个i为分界线的情况，直接更新给min即可
（6）返回min

本题优化的本质：
利用countG/R额外信息数组，加速在i位置，两头瞬间秒杀拿到G和R的个数，一下子就求出来整体需要变多少个了，这种做法我们在优化算法时常用的，空间换时间
最后一遍o(n)复杂度搞定，速度够快吧！

手撕代码：

    //复习：
    //**以i为分界线，左边：0--i，G全变R，右边：i+1--N-1的R全变G**
    public static int changeNumAtLeast(String s){
        if(s.compareTo("") == 0 || s.length() == 0) return 0;
        int N = s.length();
        //（1）countG：从**左往右**统计G的个数，目的是想让左边的全变R，所以G的个数，就是需要变为R的个数
        //（2）countR：从**右往左**统计R的个数，目的是想让右边的全变G，所以R的个数，就是需要变为G的个数
        int[] countG = new int[N];
        int[] countR = new int[N];
        char[] str = s.toCharArray();
        countG[0] = str[0] == 'G' ? 1 : 0;
        countR[N - 1] = str[N - 1] == 'R' ? 1 : 0;
        for (int i = 1; i < N; i++) {
            countG[i] = countG[i - 1] + (str[i] == 'G' ? 1 : 0);//看i处的G,括号加上，优先级在括号内
        }
        for (int i = N - 2; i >= 0; i--) {
            countR[i] = countR[i + 1] + (str[i] == 'R' ? 1 : 0);//看i处的R,括号加上，优先级在括号内
        }
        //（3）当分界线i=-1时，意味着让所有arr都变为G，所以只看R有多少个？
        // 则需要变这么多个方块：countR[i+1]=countR[0]
        int min = countR[0];
        //（4）当分界线i=N-1时，意味着让所有arr都变为R，所以只看G有多少个？
        // 则需要变这么多个方块：countG[i]=countR[N-1]
        min = Math.min(min, countG[N - 1]);
        //（5）其余i位置，左边让G变R，变这么多个：countG[i]，右边让R变G，
        // 变这么多个：countR[i+1]，即两者错位相加，看上图，
        // 最终变整体个数：countG[i]+countR[i+1]，每一个i为分界线的情况，直接更新给min即可
        for (int i = 0; i < N - 1; i++) {
            min = Math.min(min, countG[i] + countR[i + 1]);
        }
        //（6）返回min
        return min;
    }

问题不大：
测试一把：

    public static void test(){
        String s  = "RGRGR";
        String s1  = "RGRGR";
        System.out.println(changeRG(s));
        System.out.println(changeRG2(s1));
        System.out.println(changeNumAtLeast(s1));
    }

    public static void main(String[] args) {
        test();
    }
}

2
2
2

当然，可以省掉数组，咱们这样搞，拿left统计整个0–i上的G的个数，拿countR来统计i–N-1上的R的个数
这样还可以省掉一个数组
代码可以这么写，不过不是重点
重点还是上面的思想！

下面的看不看随意：

    public static int changeRG2(String s){
        //显然方法2省略了一个数组，省空间，复杂度都是差不多的
        if (s == null || s.length() == 1) return 0;

        char[] str = s.toCharArray();
        int min = Integer.MAX_VALUE;
        int N = str.length;
        int[] R = new int[N];//统计i--N-1上R的个数，从右往左统计
        R[N - 1] = str[N - 1] == 'R' ? 1 : 0;//起点
        for (int i = N - 2; i >=0; i--) {
            R[i] = R[i + 1] + (str[i] == 'R' ? 1 : 1);
        }
        //收集信息--与此同时统计0--i上G的个数
        int countG = 0;//最开始分界线i==-1，左边没有G
        min = R[0];//这个时候最小值，就是让右边全部N个都变为G，统计R【0--N-1】上的个数
        for (int i = 0; i < N - 1; i++) {
            countG += str[i] == 'G' ? 1 : 0;//累加G的个数
            min = Math.min(min, countG + R[i + 1]);//看0--i上G多少个，i+1--N-1上R多少个
        }
        //最后分界线为N时，左边全变R，看左边G多少个
        min = Math.min(min, countG + (str[N - 1] == 'G' ? 1 : 0));//这里单纯滴统计G多少个？？？
        return min;
    }

测试结果，上面已经给出了

---

总结

提示：重要经验：

1）总之都要让i做分界线，左边找G的个数N1，右边找R个数N2，整体左边变R，右边变G，就是N1+N2，每个i得到的至少要变的个数，更新给min就行
2）不管暴力解，还是优化解，都是要这么做的，而本题优化的的关键就是空间换时间，提前准备前缀统计量，在遍历i的过程中，o(1)速度拿到左右G/R的数量，这样就完成优化。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。