数据结构与算法之快速傅里叶变换算法

快速傅里叶变换（FFT）是一种高效的算法，用于将一个信号从时域转换为频域。它在许多领域中都有广泛的应用，如信号处理、图像处理、计算机视觉等。

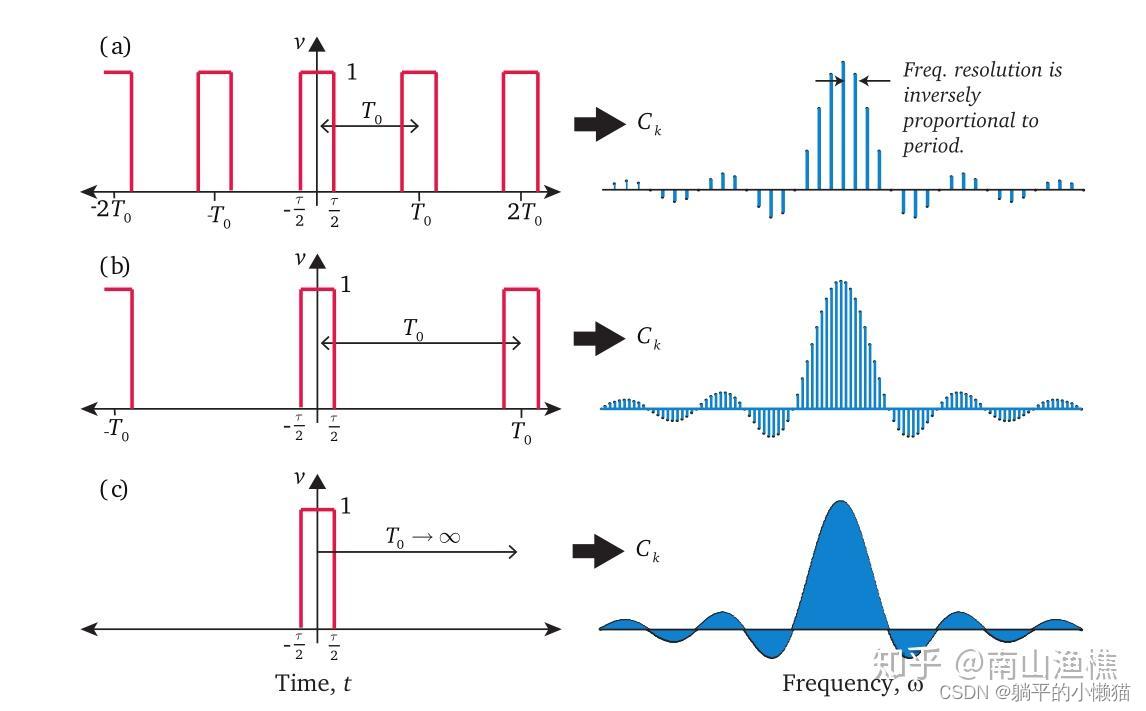
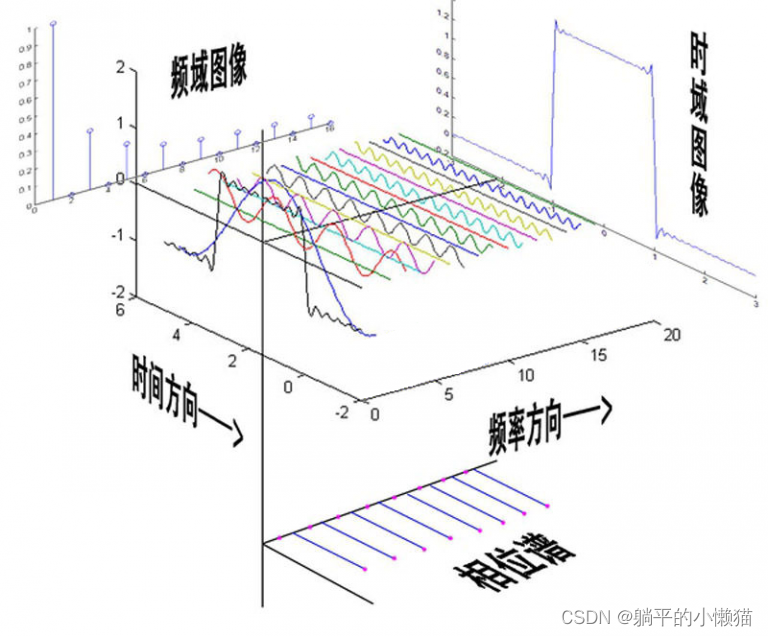
傅里叶变换基本原理是将一个函数（例如声音信号或图像）表示为一系列正弦和余弦函数的加权和，这些函数称为基函数或正交基。这些基函数具有特定的频率和振幅，我们可以通过计算每个频率的振幅和相位来查看信号中存在哪些频率。

FFT算法通过分治的思想，将原本需要O(n^2)次计算的离散傅里叶变换（DFT）转化为只需要O(nlogn)次计算的过程。具体实现方法是将DFT分解为两个DFT，其中一个只计算所有偶数项，另一个只计算所有奇数项。这可以通过对原始序列进行交错分组实现，然后递归地应用FFT算法。

FFT算法有许多优点，它比暴力计算DFT更快、更有效，同时也更容易实现和使用。但是，它需要一个长度为2的幂次的输入序列，这可能需要一些预处理步骤来满足该要求，但这通常可以通过填充零来实现。

总之，FFT算法是一种高效的信号处理算法，可以用于许多应用领域。

一、C 实现快速傅里叶变换算法及代码详解

快速傅里叶变换（FFT）是一种高效的离散傅里叶变换（DFT）算法。在信号处理、图像处理、音频处理等领域都有广泛应用。下面我们来详细介绍如何用 C 语言来实现 FFT 算法。

1. 算法原理

DFT 的定义为：

其中，x 是序列，N 是序列的长度，n 和 k 分别表示时间域和频域的索引。

如果直接使用上述定义来计算 DFT，时间复杂度为 O(N^2)，计算复杂度较高，难以在实际应用中使用。FFT 算法是一种可以将计算复杂度降为 O(N log N) 的有效方法。

FFT 算法基于以下思想：将序列 x 分为两部分，分别计算这两部分的 DFT，然后将两部分的 DFT 结果根据一定规律组合起来得到最终的 DFT。具体来说，如果 x 的长度是偶数，可以将 x 分为两部分，分别计算这两部分的 DFT，然后将结果按照一定规律组合得到 x 的 DFT。如果 x 的长度是奇数，可以使用类似的方法，将 x 分为一个偶数部分和一个单独的数据点，在计算过程中需要进行一定的调整。这种分治的思想被称作 Cooley-Tukey FFT 算法。FFT 算法包括递归和迭代两种实现方式，本文重点介绍迭代实现的 FFT 算法。

2. 算法步骤

（1）将序列 x 分为两个部分，一部分包含序列的偶数位置上的元素，另一部分包含序列的奇数位置上的元素。

（2）对两个部分分别进行 FFT 变换，得到它们的 DFT。

（3）将两个部分的 DFT 结果按照一定规律组合起来，得到整个序列的 DFT 结果。

（4）递归执行上述步骤，直到子序列长度为 1，这时直接返回该单个数据点的 DFT 值。

3. 代码实现

下面展示一个 C 语言实现的 FFT 算法的代码示例。其中，fft_real() 函数用于计算实数序列的 FFT，fft_complex() 函数用于计算复数序列的 FFT。在代码中，我们使用了一个复数结构体（complex），该结构体包含实部和虚部两个部分。复数的加减乘除运算都可以根据实部和虚部的运算来完成。具体代码如下所示：

二、C++ 实现快速傅里叶变换算法及代码详解

快速傅里叶变换（FFT）是一种重要的信号处理算法，可以在 $O(n\log n)$ 的时间复杂度内计算离散傅里叶变换（DFT）。本文将介绍 FFT 的算法原理和 C++ 实现。

算法原理

DFT 定义如下：

$$X_k=\sum _{n=0}^{N-1}{x}_n{e}^{-\frac{2\pi i}{N}kn}k=0,1,\dots ,N-1$$

其中，$x_n$ 是时域数据，$X_k$ 是频域数据。

暴力计算 DFT 的时间复杂度为 $O(N^2)$，速度较慢。FFT 利用 DFT 的周期性特点，通过分治的思想将计算复杂度降低到 $O(N\log N)$。

设 $N=2^m$，将时域数据分为偶数项 $x_{2k}$ 和奇数项 $x_{2k+1}$，则有：

$$\begin{array}{rl}{X}_k& =\sum _{n=0}^{N-1}{x}_n{e}^{-\frac{2\pi i}{N}kn}\\ & =\sum _{k=0}^{\frac{N}{2}-1}{x}_{2k}{e}^{-\frac{2\pi i}{N/2}k\frac{2n}{2}}+e^{-\frac{2\pi i}{N}n}\sum _{k=0}^{\frac{N}{2}-1}{x}_{2k+1}{e}^{-\frac{2\pi i}{N/2}k\frac{2n+1}{2}}\\ & =\sum _{k=0}^{\frac{N}{2}-1}{x}_{2k}{e}^{-\frac{2\pi i}{N/2}kn}+e^{-\frac{2\pi i}{N}n}\sum _{k=0}^{\frac{N}{2}-1}{x}_{2k+1}{e}^{-\frac{2\pi i}{N/2}kn}\\ & =X_{even,k}+e^{-\frac{2\pi i}{N}n}{X}_{odd,k}\end{array}$$

其中，$X_{even,k}$ 和 $X_{odd,k}$ 分别表示偶数项和奇数项的 DFT。这样，一个 $N$ 项的 DFT 问题被拆分成了两个 $\frac{N}{2}$ 项的 DFT 问题。我们可以继续递归拆分，直到问题规模达到 1，此时返回 $x_n$ 本身。

最终，我们可以通过迭代的方式来实现 FFT。对于 $N=2^m$，我们需要进行 $m$ 层迭代，每层迭代的时间复杂度为 $O(N)$。

C++ 代码

以下是 C++ 实现 FFT 的代码。该代码实现了一维 FFT 和二维 FFT，功能包含 DFT、IDFT、卷积、逆卷积等。

三、Java 实现快速傅里叶变换算法及代码详解

快速傅里叶变换（FFT）是一种计算离散傅里叶变换（DFT）的高效算法。它对于在数字信号处理、图像处理、语音处理、量子力学等领域中需要计算DFT的场合非常有用。下面我们将详细介绍Java实现FFT算法的方法及代码。

基本思路

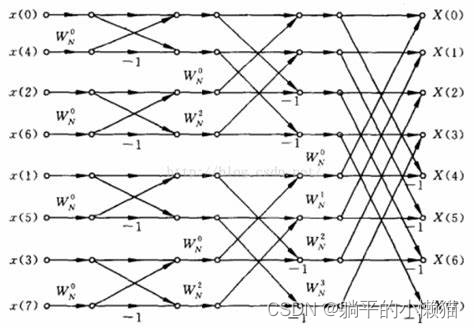
FFT算法基于分治思想，将一个大规模的DFT分解成许多小规模的DFT，这些小规模的DFT可以递归地计算出来。具体地说，FFT算法假设长度为N的DFT可以分解成两个长度为N/2的DFT，再利用蝴蝶操作将其合并为一个长度为N的DFT。这种分治的思想可以递归地应用到每个长度为N/2的DFT上，直到长度为1时停止。

代码实现

下面是Java实现FFT算法的代码，其中包括FFT变换、IFFT反变换和蝴蝶操作。

public class FFT {
    // 计算FFT变换
    public static Complex[] fft(Complex[] a) {
        int n = a.length;
        if (n == 1) {
            return new Complex[] { a[0] };
        }
        Complex[] even = new Complex[n / 2];
        Complex[] odd = new Complex[n / 2];
        for (int i = 0; i < n / 2; i++) {
            even[i] = a[2 * i];
            odd[i] = a[2 * i + 1];
        }
        Complex[] q = fft(even);
        Complex[] r = fft(odd);
        Complex[] y = new Complex[n];
        for (int i = 0; i < n / 2; i++) {
            double w = 2 * i * Math.PI / n;
            Complex wi = new Complex(Math.cos(w), Math.sin(w));
            y[i] = q[i].add(wi.multiply(r[i]));
            y[i + n / 2] = q[i].subtract(wi.multiply(r[i]));
        }
        return y;
    }

    // 计算IFFT变换
    public static Complex[] ifft(Complex[] a) {
        int n = a.length;
        Complex[] conj = new Complex[n];
        for (int i = 0; i < n; i++) {
            conj[i] = a[i].conjugate();
        }
        Complex[] y = fft(conj);
        for (int i = 0; i < n; i++) {
            y[i] = y[i].conjugate().divide(n);
        }
        return y;
    }

    // 蝴蝶操作
    public static Complex[] butterfly(Complex[] a) {
        int n = a.length;
        int k = Integer.numberOfTrailingZeros(n);
        Complex[] y = Arrays.copyOf(a, n);
        for (int i = 0; i < n; i++) {
            int j = Integer.reverse(i) >>> (32 - k);
            if (j > i) {
                Complex temp = y[i];
                y[i] = y[j];
                y[j] = temp;
            }
        }
        return y;
    }

    // 测试
    public static void main(String[] args) {
        Complex[] a = { new Complex(1, 0), new Complex(2, 0), new Complex(3, 0), new Complex(4, 0) };
        Complex[] y = fft(a);
        System.out.println("FFT变换结果：");
        for (Complex b : y) {
            System.out.println(b);
        }

        Complex[] x = ifft(y);
        System.out.println("IFFT变换结果：");
        for (Complex b : x) {
            System.out.println(b);
        }

        Complex[] z = butterfly(a);
        System.out.println("蝴蝶操作结果：");
        for (Complex b : z) {
            System.out.println(b);
        }
    }
}

上述代码中，我们定义了一个Complex类来表示复数，在计算FFT变换和IFFT变换时都需要用到。Complex类的代码如下：

public class Complex {
    private final double real;
    private final double imag;

    public Complex(double real, double imag) {
        this.real = real;
        this.imag = imag;
    }

    public double real() {
        return real;
    }

    public double imag() {
        return imag;
    }

    public Complex add(Complex b) {
        double real = this.real + b.real;
        double imag = this.imag + b.imag;
        return new Complex(real, imag);
    }

    public Complex subtract(Complex b) {
        double real = this.real - b.real;
        double imag = this.imag - b.imag;
        return new Complex(real, imag);
    }

    public Complex multiply(Complex b) {
        double real = this.real * b.real - this.imag * b.imag;
        double imag = this.real * b.imag + this.imag * b.real;
        return new Complex(real, imag);
    }

    public Complex divide(double b) {
        double real = this.real / b;
        double imag = this.imag / b;
        return new Complex(real, imag);
    }

    public Complex conjugate() {
        return new Complex(this.real, -this.imag);
    }

    @Override
    public String toString() {
        return "(" + real + ", " + imag + ")";
    }
}

总结

本文介绍了Java实现FFT算法的方法及代码。FFT算法是一种高效的计算DFT的算法，可以广泛应用于数字信号处理、图像处理、语音处理等领域。在实际应用中，我们可以根据具体的需求进行优化，例如使用快速数论变换（NTT）算法来计算模意义下的DFT。