算法训练Day42 | 01背包问题的理论基础（二维和一维dp数组的全面剖析）；LeetCode416. 分割等和子集（01背包的应用）

本文深入探讨了01背包问题，包括二维和一维动态规划数组的实现，以及如何在LeetCode416题中应用01背包理论。文章详细阐述了动态规划五部曲，强调了初始化和遍历顺序的重要性，并通过实例展示了dp数组的推导过程。此外，还讨论了一维dp数组的滚动优化，解释了为何必须倒序遍历背包容量。最后，文章分析了LeetCode416题的解决方案，将其转化为01背包问题。

01背包问题的理论基础

背包问题系列：

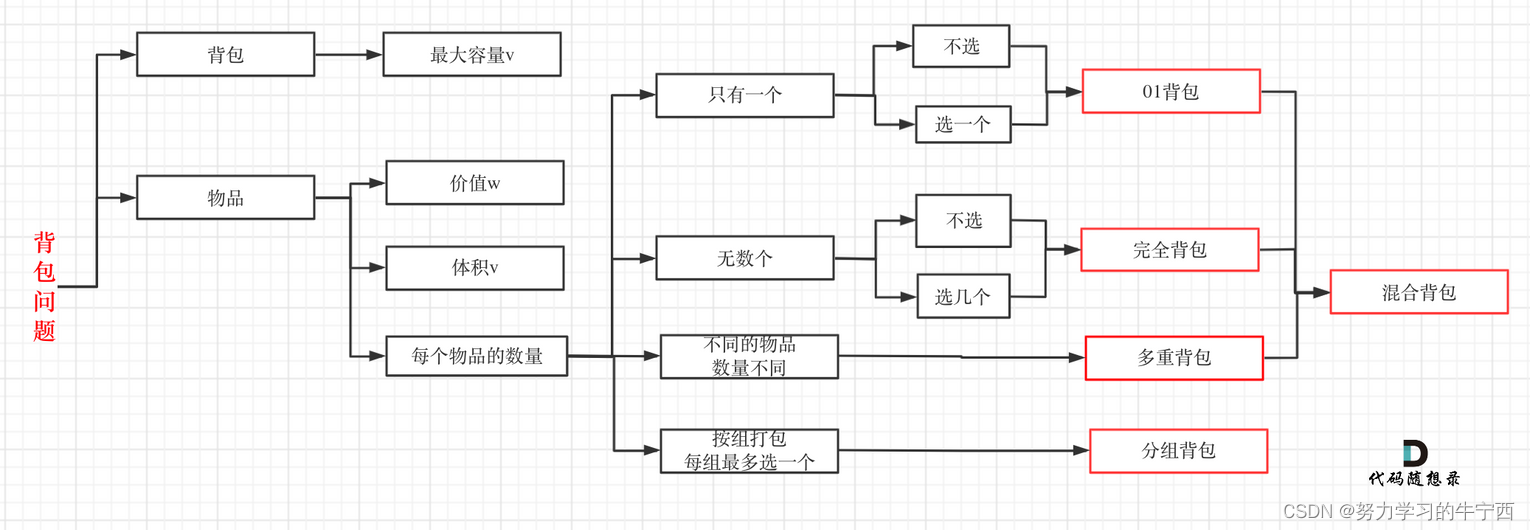
对于面试的话，其实掌握01背包，和完全背包，就够用了，最多可以再来一个多重背包；至于其他背包，面试几乎不会问，都是竞赛级别的了，leetcode上连多重背包的题目都没有，所以题库也告诉我们，01背包和完全背包就够用了；

而完全背包又是也是01背包稍作变化而来，即：完全背包的物品数量是无限的，**所以背包问题的理论基础重中之重是01背包，一定要理解透！**leetcode上没有纯01背包的问题，都是01背包应用方面的题目，也就是需要转化为01背包问题。所以我先通过纯01背包问题，把01背包原理讲清楚，后续再讲解leetcode题目的时候，重点就是讲解如何转化为01背包问题了。

题目描述

（LeetCode上没有纯粹的01背包问题）

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

方法一：二维dp数组01背包

1. 思路

这是标准的背包问题，以至于很多同学看了这个自然就会想到背包，甚至都不知道暴力的解法应该怎么解了。这样其实是没有从底向上去思考，而是习惯性想到了背包；

那么暴力的解法应该是怎么样的呢？

每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是o(2^n)，这里的n表示物品数量。所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！

讲解所用到的例子：

背包最大重量为4，物品如下：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？以下讲解和图示中出现的数字都是以这个例子为例。

动态规划五部曲

1.1 确定dp数组以及下标的含义

对于背包问题，有一种写法，是使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

只看这个二维数组的定义，大家一定会有点懵，看下面这个图：

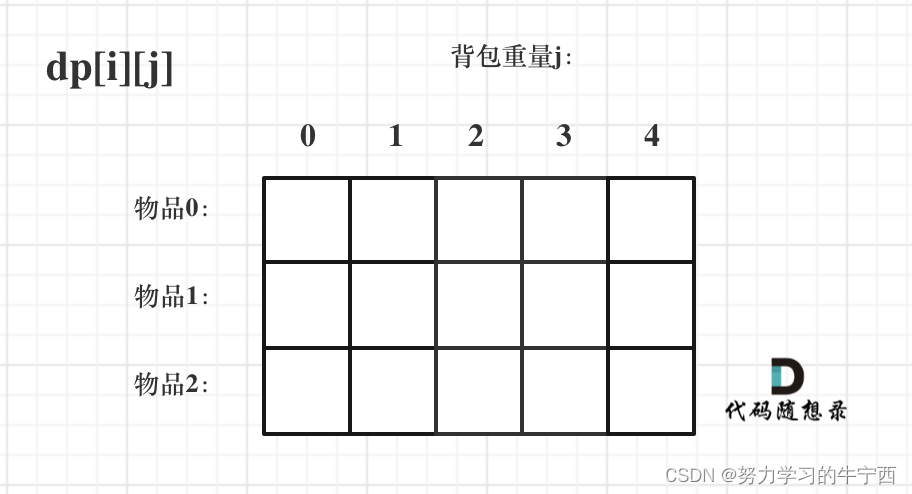
要时刻记着这个dp数组的含义，下面的一些步骤都围绕这dp数组的含义进行的 ，如果哪里看懵了，就来回顾一下i代表什么，j又代表什么。

1.2 确定递推公式

再回顾一下dp[i][j]的含义：从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少，那么可以有两个方向推出来dp[i][j]：

不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。)
放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值；

所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

1.3 dp数组如何初始化

关于初始化，一定要和dp数组的定义吻合，否则到递推公式的时候就会越来越乱，首先回顾一下递推公式，看看到底要初始化那些元素？

💡 递归公式： dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

如果要得到dp[i][j]，就要知道dp[i - 1][j]和dp[i - 1][j - weight[i]] ；dp[i - 1][j]在dp[i][j]的正上方，dp[i - 1][j - weight[i]]在dp[i][j]的左上方；

看清楚位置之后，我们就知道了，需要初始化的是这个矩阵的第一行以及第一列：

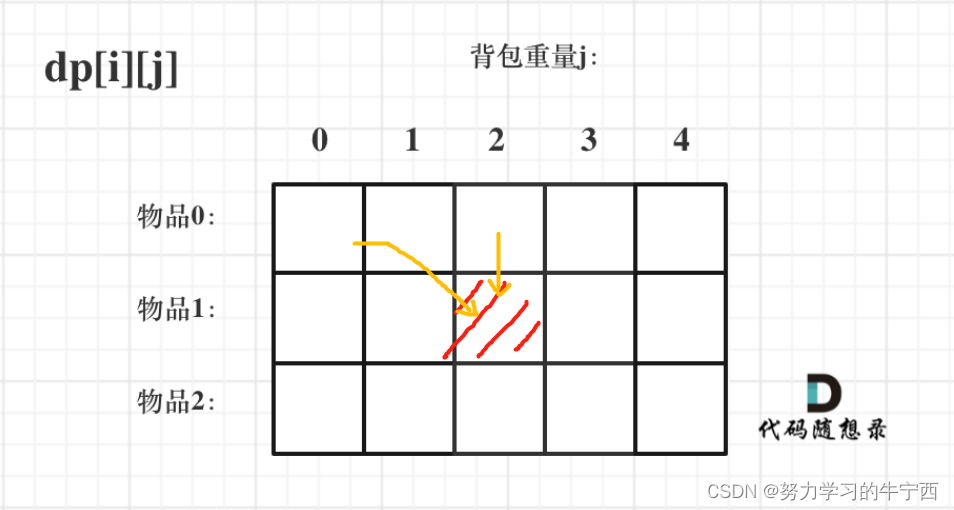
首先看第一列

如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。如图：

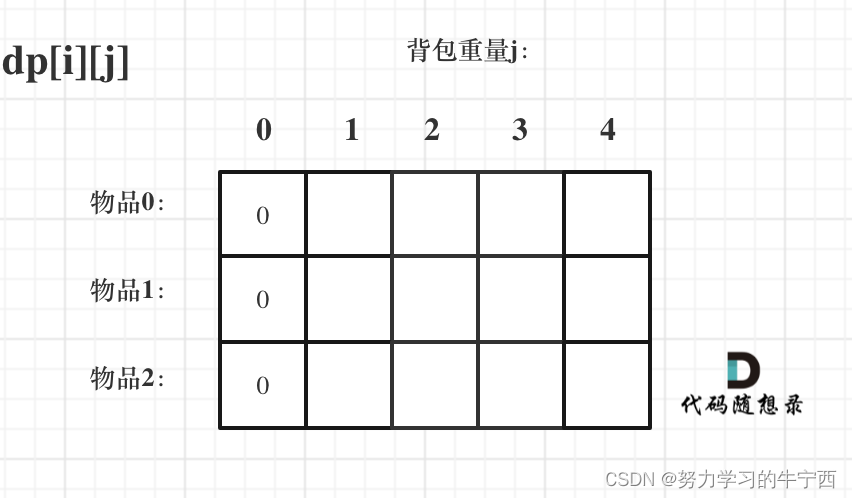
再看第一行

dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值；

那么很明显当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小；
当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。

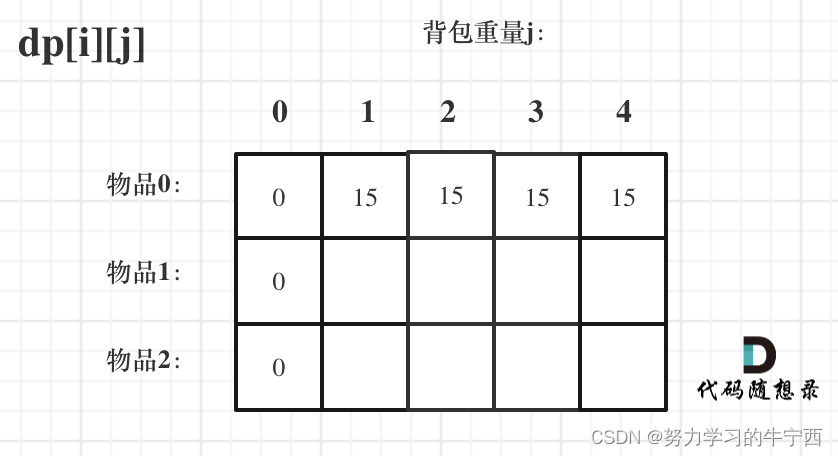
其他位置怎么初始化？

dp[0][j] 和 dp[i][0]