手撕算法

最新推荐文章于 2024-04-27 07:55:38 发布
最新推荐文章于 2024-04-27 07:55:38 发布
阅读量1k 收藏 1
点赞数
分类专栏： 学习记录 文章标签： 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_47645663/article/details/114693631
版权
本文详细介绍了动态规划在解决最短路径、最长递增子序列、三角形最小路径和等问题的应用，以及链表操作，如反转链表、求交点、求环、复制复杂链表等。通过实例解析算法思路，提供了优化的空间复杂度和时间复杂度分析，并展示了相关代码实现。
摘要由CSDN通过智能技术生成

手撕面试高频算法

在这里插入图片描述

标注*号的就是还没写完的题目


动态规划

1、最小路径和 ✔

最小路径和

思路:

  1. n为行数，m为列数，设dp[][] 为n×m的矩阵， dp[i][j] 就是走到该位置的最小路径和
  2. 确定边界：
    - 当 i = 0 ，j ≠ 0 时，只能从左边来，所以 grid[i][j] += grid[i][j-1];
    - 当 i ≠ 0 ，j = 0 时，只能从上边来，所以 grid[i][j] += grid[i-1][j];
    - 除去上面两种情况，其他都可以从上边或左边过来，这时候就要选择路径和更小的那个：
    grid[i][j] += Math.min( grid[i-1][j] , grid[i][j-1] );
  3. 通过观察可以发现我们可以直接在原矩阵的基础上进行修改，而不需要占用额外的空间。

代码：

public int minPathSum(int[][] grid) {
   
        int n = grid.length,m = grid[0].length;
        
        for(int i = 0;i < n;i++){
      //行
            for(int j = 0;j < m;j++){
      //列
                if(i == 0 && j == 0) continue;
                else if(i == 0){
   
                    //第一行,只能从左边来
                    grid[i][j] += grid[i][j-1]; 
                }else if(j == 0){
   
                    //第一列,只能从上边来
                    grid[i][j] += grid[i-1][j]; 
                }else{
   
                    //非第一行第一列 需要判断哪边的值更小,就加哪边
                    grid[i][j] += Math.min(grid[i-1][j],grid[i][j-1]);
                }
            }
        }

        return grid[n-1][m-1];
    }

复杂度分析：

  • 时间复杂度：O(n*m)，需要遍历整个矩阵一次
  • 空间复杂度：O(1)



2、最长递增子序列 ✔

最长递增子序列

参考答案

这道题考虑使用动态规划：

我们定义dp[i]为当前index = i时数组的最长严格递增子序列长度。关键的问题在于我们怎么去计算dp数组的每个值。

状态转移公式

假设我们已经知道了 dp[0…4] 的所有结果，我们如何通过这些已知结果推出 dp[5] 呢？
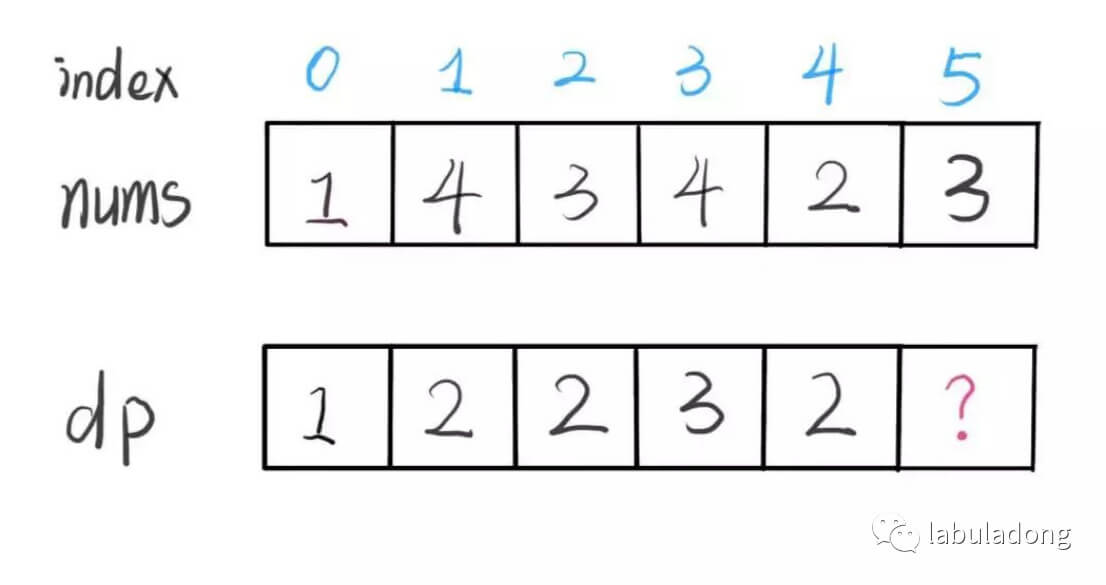
在这里插入图片描述
很明显，nums[5] = 3，既然是递增子序列，我们只要找到前面那些结尾比 3 小的子序列，然后把 3 接到最后，就可以形成一个新的递增子序列，再将这个新的子序列长度加一

显然，可能形成很多种新的子序列，但是我们只选择最长的那一个，把最长子序列的长度作为 dp[5] 的值即可。

https://pic.leetcode-cn.com/8fe73d010abfdbb0ff4950e96640bb8a04391fc7438fed845ab6d36208468266.gif

所以这道题我们需要做的有：

  • 在刚开始时定义 dp[i] = 1，因为最短的序列就是单独一个数字
  • 遍历数组的时候，比较 i（后） 与 j （前），如果 nums[i] > nums[j] 则 nums[i] 可以接上 nums[j] 成为一个更长的递增子序列。我们就可以让 dp[i] = Math.max(dp[i],dp[j]+1) <– 如果这一步能想明白，那么整道题就迎刃而解

代码：

public int lengthOfLIS(int[] nums) {
   
        int n = nums.length;
        int[] dp = new int[n];
        Arrays.fill(dp, 1);   //将数组全部替换成1
        for (int i = 0; i < n; i++) {
   
            for (int j = 0; j < i; j++) {
   
                if (nums[i] > nums[j]) {
   
                    dp[i] = Math.max(dp[i], dp[j] + 1);   //最重要的公式，求出最长的递增子序列
                }
            }
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
   
            ans = Math.max(ans, dp[i]);   //遍历取出最大值
        }
        return ans;
    }

复杂度分析：

  • 时间复杂度：O(n^2)，其中 n 为数组 nums 的长度。动态规划的状态数为 n，计算状态 dp[i] 时，需要 O(n) 的时间遍历 dp[0…i−1] 的所有状态，所以总时间复杂度为 O(n^2)
  • 空间复杂度：O(n)，需要额外使用长度为 n 的 dp 数组。



3、三角形 ✔

三角形最小路径和

思路：

  1. 使用动态规划，定义 dp[][] ，大小为n行m列，dp[i][j] 就是走到该位置的最小路径和
  2. 确定边界： i为行数
    - 当 j = 0 时，只能从 j 来，所以 triangle.get(i).set ( j , triangle.get(i).get(j) + triangle.get(i-1).get(j));
    - 当 j = i 时，只能从 j-1 来，所以 triangle.get(i).set ( j , triangle.get(i).get(j) + triangle.get(i-1).get(j-1));
    - 除去上面两种情况，其他都可以从 j 或 j-1 过来，这时候就要选择路径和更小的那个：
    int min = Math.min ( triangle.get(i-1).get(j) , triangle.get(i-1).get(j-1) );
    triangle.get(i).set ( j , triangle.get(i).get(j) + min);
  3. 当 i=n-1 时，即为最后一行，我们需要维护一个最小路径和ans

代码：

public int minimumTotal(List<List<Integer>> triangle) {
   
        int n = triangle.size();
        if(n == 1) return triangle.get(0).get(0);   // 如果只有一行
        int ans = Integer.MAX_VALUE;   
        for(int i=1;i < n;i++){
       //从第二行开始遍历
            for(int j = 0;j <= i;j++){
   
                // 列为0，即在左边，只能从j下来
                if(j == 0) triangle.get(i).set(j,triangle.get(i).get(j) + triangle.get(i-1).get(j));
                // 列为i，即在右边，只能从j-1下来
                else if(j == i) triangle.get(i).set(j,triangle.get(i).get(j) + triangle.get(i-1).get(j-1));
                // 列在中间，可以从j或j-1下来 需要判断
                else{
   
                    int min = Math.min(triangle.get(i-1).get(j),triangle.get(i-1).get(j-1));
                    triangle.get(i).set(j,triangle.get(i).get(j) + min);
                }
                if(i == n-1) ans = Math.min(ans,triangle.get(i).get(j));   //最后一行，维护最小答案
            }
        }    
        return ans;
    }

运行结果：
在这里插入图片描述

复杂度分析：

  • 时间复杂度：O(n^2)，n为三角形行数，并且在更改原集合的情况下，我们频繁使用get和set方法，也会消耗一定的性能
  • 空间复杂度：O(1)

看了题解之后的答案：

定义二维 dp 数组，自底向上的递推

状态定义：

dp[i][j] 表示从点 (i, j)到底边的最小路径和

状态转移方程（自底向上）：

dp[i][j] = min(dp[i+1][j],dp[i+1][j+1]) + triangle[i][j]

代码：

public int minimumTotal(List<List<Integer>> triangle) {
   
        int n = triangle.size();
        // dp[i][j] 表示从点 (i, j) 到底边的最小路径和。
        int[][] dp = new int[n + 1][n + 1];
        // 从三角形的最后一行开始递推。
        for (int i = n - 1; i >= 0; i--) {
   
            for (int j = 0; j <= i; j++) {
   
                dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle.get(i).get(j);
            }
        }
        return dp[0][0];
    }

复杂度分析：

  • 时间复杂度：O(N^2)，N 为三角形的行数
  • 空间复杂度：O(N^2)，N 为三角形的行数

空间优化：
在上述代码中，我们定义了一个 N 行 N 列 的 dp 数组
但是在实际递推中我们发现，计算 dp[i][j] 时，只用到了下一行的 dp[i + 1][j] 和 dp[i + 1][j + 1]
因此 dp 数组不需要定义 N 行，只要定义 1 行就足够：

public int minimumTotal(List<List<Integer>> triangle) {
   
        int n = triangle.size();
        int[] dp = new int[n + 1];   //用于防止j+1越界
        for (int i = n - 1; i >= 0; i--) {
   
            for (int j = 0; j <= i; j++) {
   
                dp[j] = Math.min(dp[j], dp[j + 1]) + triangle.get(i).get(j);
            }
        }
        return dp[0];
    }

复杂度分析：

  • 时间复杂度：O(N^2)，N 为三角形的行数
  • 空间复杂度：O(N)，N 为三角形的行数



4、找零钱 ✔

零钱兑换

答案看的这个

思路:

  1. dp[j] 代表的含义：就是amount在这个coins组合下最少用多少枚硬币

可以转化为完全背包问题 ： 填满容量为amount的背包最少需要多少硬币

  1. 初始化dp的问题：后面要求的是最少的硬币，所以初始化不能对结果造成影响，而因为硬币的数量一定不会超过amount（面值最低为1），所以直接初始化dp数组的值为amount+1，特例 dp[0] = 0;

  2. 最重要的转移方程： dp[j] = Math.min(dp[j], dp[j-coin] + 1)
    当前填满容量j最少需要的硬币 = min( 之前填满容量j最少需要的硬币, 填满容量 j - coin 需要的硬币 + 1个当前硬币）

  3. 返回dp[amount]，如果dp[amount]的值为10001没有变过，说明找不到硬币组合，返回-1

代码：

public int coinChange(int[] coins, int amount) {
   
        int a = amount + 1;   
        int[] dp = new int[a];  //定义amount+1
        Arrays.fill(dp, a);  //因为硬币的数量一定不会超过amount
        dp[0] = 0;   //当amount == 0 时 返回0
        for(int coin : coins){
   
            for(int j = coin; j < a; j++){
      //从每个硬币的面值开始遍历到amount
                    dp[j] = Math.min(dp[j], dp[j - coin] + 1);  
                   //这个转移方程就是dp[amount]在这个coins组合下最少用多少枚硬币
            }
        }
        return dp[amount] == a ? -1 : dp[amount];
    }



零钱兑换 II

–> 答案参考

思路：

  1. dp[j] 代表 j 金额 在当前的 coins 组合下有多少种组合方式

也可转化为完全背包之组合问题——dp[j] 代表装满容量为j的背包有几种硬币组合

  1. 列出转移方程：dp[j] = dp[j] + dp[j - coin]
    当前填满 j 容量的方法数 = 之前填满 j 容量的硬币组合数 + 填满 j - coin 容量的硬币组合数
    也就是当前硬币coin的加入，可以把 j - coin 容量的组合数加入进来
  2. dp[0] = 1; 即金额为0时只有一种组合coins的方式（都不用）

代码：

public int change(int amount, int[] coins) {
   
        // dp[j] 代表 amount金额 在当前的 coins 组合下有多少种组合方式
        int[] dp = new int[amount+1];
        dp[0] = 1;
        for(int coin:coins){
   
            for(int j = coin;j < amount+1;j++){
   
                dp[j] = dp[j] + dp[j-coin];
            }
        }
        return dp[amount];
    }



5、最大字段和 ✔

最大子序和

这道题要我们找到一个具有最大和的连续子数组，可以转换为求以 i 结尾的连续子数组的最大和，考虑使用动态规划，列出转移方程：dp[i] = Math.max( dp[i-1]+nums[i] , nums[i] )，遍历数组输出dp[ ]最大值即可

代码：

public int maxSubArray(int[] nums) {
   
       //dp[i]表示下标j的连续子数组最大和
       int n = nums.length,ans = nums[0];
       int[] dp = new int[n];
       dp[0] = nums[0];
       for(int i = 0;i < n;i++){
   
            if(i != 0) dp[i] = Math.max(nums[i],dp[i-1]+nums[i]);
            ans = Math.max(dp[i],ans);
       } 
       return ans;
    }

但是通过观察我们可以发现，dp数组每次都只会使用dp[i]，我们可以考虑用一个数字pre代替dp数组，改进后的代码：

public int maxSubArray(int[] nums) {
   
        //简化 --> pre为前一个数的连续子数组最大和  
       int pre = 0,ans = nums[0];
       for(int num:nums){
   
           pre = Math.max(num,num+pre);
           ans = Math.max(ans,pre);
       }
       return ans;
    }

复杂度分析：

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)



6、爬楼梯 ✔

爬楼梯

通过观察可知该题为斐波那契数列，根据数列特性可写出递归代码：

public int climbStairs(int n) {
   
        if(n == 1) return 1;
        if(n == 2) return 2;
        return climbStairs(n-1)+climbStairs(n-2);
    }

这样实现算法时空复杂度很高，并且有可能会导致栈溢出。

考虑使用正向循环（滚动数组）：

public int climbStairs(int n) {
   
        int a=0,b=0,sum=1;
        for(int i=1;i<=n;i++){
   
            a = b;
            b = sum;
            sum = a+b;
        }
        return sum;
    }

复杂度分析：

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)



7、分割等和子集 ✔

分割等和子集

题解

思路：

  1. 特例： 如果sum为奇数，那一定找不到符合要求的子集，返回False

  2. dp[j]含义： 有没有和为j的子集，有为True，没有为False

  3. 初始化dp数组： 长度为target + 1，用于存储子集的和从0到target是否可能取到的情况。
    比如和为0一定可以取到（也就是子集为空），那么dp[0] = True

  4. 接下来开始遍历nums数组，对遍历到的数nums[i]有两种操作，一个是选择这个数，一个是不选择这个数。

    • 不选择这个数：dp不变
    • 选择这个数：dp中已为True的情况再加上nums[i]也为True。比如dp[0]已经为True，那么dp[0 + nums[i]]也是True

  5. 在做出选择之前，我们先逆序遍历子集的和从nums[i]到target的所有情况，判断当前数加入后，dp数组中哪些和的情况可以从False变成True

    （为什么要逆序：是因为dp后面的和的情况是从前面的情况转移过来的，如果前面的情况因为当前nums[i]的加入变为了True，比如dp[0 + nums[i]]变成了True，那么因为一个数只能用一次，dp[0 + nums[i] + nums[i]]不可以从dp[0 + nums[i]]转移过来。如果非要正序遍历，必须要多一个数组用于存储之前的情况。而逆序遍历可以省掉这个数组）

    状态转移方程： dp[j] = dp[j] or dp[j - nums[i]]

    • 如果不选择当前数，那么和为j的情况保持不变，dp[j]仍然是dp[j]，原来是True就还是True，原来是False也还是False；
    • 如果选择当前数，那么如果j - nums[i]这种情况是True的话和为j的情况也会是True。比如和为0一定为True，只要 j - nums[i] == 0，那么dp[j]就变成了True

    dp[j]和dp[j-nums[i]]只要有一个为True，dp[j]就变成True，因此用or连接两者

  6. 返回dp[target]

代码：

public boolean canPartition(int[] nums) {
   
        // 求出 sum 
        int sum = Arrays.stream(nums).sum();;
        // sum为奇数 说明不能分割为两个相等的子集
        if(sum % 2 == 1) return false;

        int target = sum >> 1;
        boolean[] dp = new boolean[target + 1];
        dp[0] = true;
        for(int num : nums){
   
            for(int j = target; j >= num; j--){
   
                dp[j] = dp[j] || dp[j - num];
            }
        }

        return dp[target];
    }

复杂度分析：

  • 时间复杂度：O(n * target)
  • 空间复杂度：O(target)



8、目标和 ✔

目标和

这道题用枚举递归也能做：

class Solution {
   

    int count = 0;
    public int findTargetSumWays(int[] nums, int S) {
   
        forSum(nums,S,0);
        return count;
    }

    public void forSum(int[] nums,int S,int i){
   
        if(S == 0 && i == nums.length){
   
            count ++;
            return;
        }

        if(i == nums.length) return;

        forSum(nums,S + nums[i],i + 1);
        forSum(nums,S - nums[i],i + 1);
    }
}

但是用递归时间复杂度是O(2^n)，其中n是数组nums的长度，时间复杂度为指数级别，效率比较差。

我们再看看dp：

大佬题解

思路：

  1. 01背包问题是选或者不选，但本题是必须选，是选+还是选-。先将本问题转换为01背包问题。
    假设所有符号为+的元素和为x，符号为-的元素和的绝对值是y
    我们想要的 S = 正数和 - 负数和 = x - y
    而已知x与y的和是数组总和：sum = x + y
    可以求出 x = (S + sum) / 2 = target
    也就是我们要从nums数组里选出几个数，令其和为target
    于是就转化成了求容量为target的01背包问题 => 要装满容量为target的背包，有几种方案
  2. 特例判断
    如果S大于sum，不可能实现，返回0
    如果x不是整数，也就是S + sum不是偶数，不可能实现，返回0
    比如： nums: [1, 1, 1, 1, 1], S: 4 => 无解
  3. dp[j]代表的意义：填满容量为j的背包，有dp[j]种方法。因为填满容量为0的背包有且只有一种方法，所以dp[0] = 1
  4. 状态转移：dp[j] = dp[j] + dp[j - num]，
    当前填满容量为j的包的方法数 = 之前填满容量为j的包的方法数 + 之前填满容量为j - num的包的方法数
    也就是当前数num的加入，可以把之前和为j - num的方法数加入进来。
  5. 返回dp[target]

代码：

public int findTargetSumWays(int[] nums, int S) {
   
        // 求出sum
        int sum = 0;
        for(int num : nums){
   
            sum += num;
        }

        // 特例判断
        if(S > sum || (sum + S) % 2 == 1) return 0;

        int target = (sum + S) >> 1;
        int[] dp = new int[target + 1];
        dp[0] = 1;
        // 状态转移：dp[j] = dp[j] + dp[j - num]
        for(int num : nums){
   
            for(int j = target; j >= num; j--){
   
                dp[j] = dp[j] + dp[j - num];
            }
        }
        return dp[target];
    }

复杂度分析：

  • 时间复杂度：O(n * target)
  • 空间复杂度：O(target)





链表

1、链表逆序(反转链表) ✔

反转链表
在这里插入图片描述

class Solution {
   
    public ListNode reverseList(ListNode head) {
   
        ListNode pre = null,cur = head;
        ListNode temp = new ListNode(0);
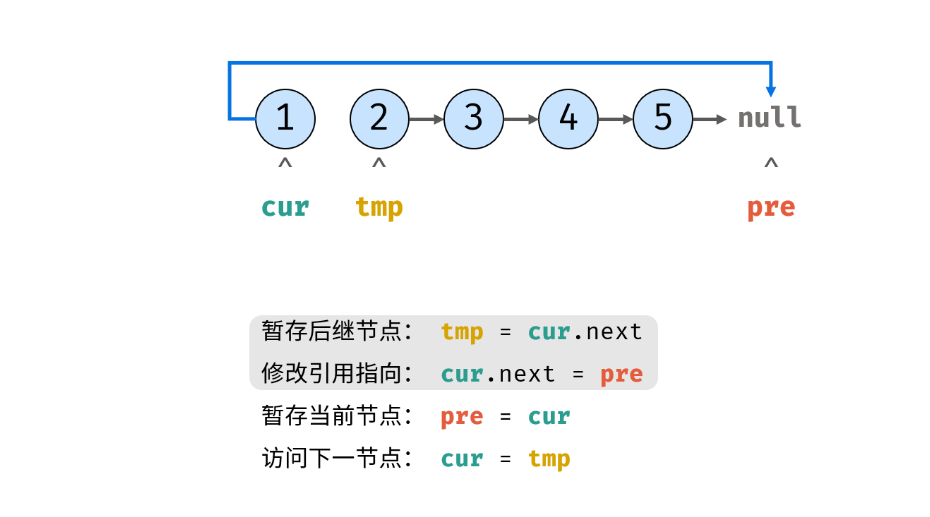
        while(cur != null){
   
            temp = cur.next;     //暂存后继节点
            cur.next = pre;      //更改指向
            pre = cur;           //更新pre
            cur = temp;          //访问下一节点
        }
        return pre;
    }
}

复杂度分析：

  • 时间复杂度：O(a+b),最差情况下（即 |a - b| = 1 , c=0 ），此时需遍历 a+b 个节点。
  • 空间复杂度：O(1)



反转链表 II

思路:

  • 使用一个count记录，把要反转的链表拿出来
  • 对链表进行反转
  • 将反转的链表接回原链表
    在这里插入图片描述

结果看起来还行，但是自己思考的思路比较复杂，看了题解之后发现有更简洁的写法：

题解

思路：

  1. 建一个虚拟头节点dummy，指向head节点
  2. 建立hh指针，一直往右移动至left的前一位置
  3. 使用a、b指针，将目标节点的next指针翻转
  4. 让hh.next（也就是left节点）的next指针指向b
  5. 让hh的next指针指向a
  6. 返回dummy.next

代码：

public ListNode reverseBetween(ListNode head, int l, int r) {
   
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        r -= l;    // 调整r指针 变成要被反转的链表的步数
        ListNode hh = dummy;
        
        while (l-- > 1) hh = hh.next;     
        // ↑ 使hh指针在要被反转的前一个位置上,此时a在翻转链表的第一个元素,b在第二个
        ListNode a = hh.next, b = a.next;
        
        while (r-- > 0) {
      // 每走一步 r--
            ListNode tmp = b.next;  
            b.next = a;
            a = b;
            b = tmp;
        }
        
        hh.next.next = b;
        hh.next = a;
        return dummy.next;
    }



2、链表求交点 ✔

相交链表
在这里插入图片描述

public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
   
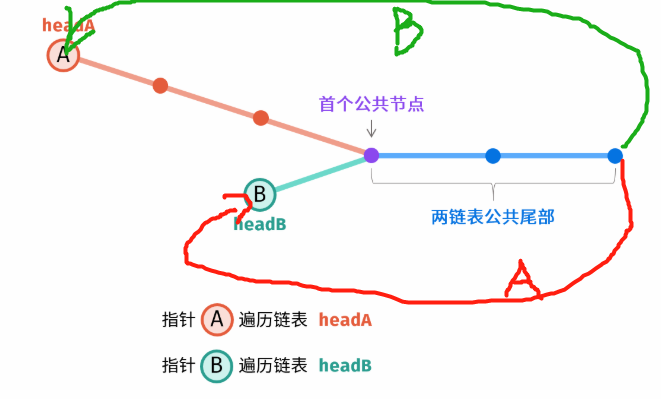
        //双指针  在A的尾部衔接上B  两个指针一起走  
        //最后如果相同就返回A  不相同走到最后 A B均为null
        ListNode A = headA, B = headB;
        while (A != B) {
   
            A = A != null ? A.next : headB;
            B = B != null ? B.next : headA;
        }
        return A;

        //另外一个版本的双指针  如果A比B长 就先让A走(A-B)步 再双指针遍历 
        //如果有相同点返回A 没有相同点返回null   比较麻烦
    }

复杂度分析：

  • 时间复杂度：O(N)
  • 空间复杂度：O(1)



3、链表求环(环形链表) ✔

环形链表

同样使用双指针求解,快慢指针一起遍历链表,如果两指针相遇则说明存在环,反之则不存在

public boolean hasCycle(ListNode head) {
   
        if(head == null) return
最低0.47元/天 解锁文章
赤埋
关注
  • 0
    点赞
  • 踩
  • 1
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
专栏目录
手撕常用算法
haoyu_zhang的博客
01-05 1439
手撕常用算法 1-1枚举类型-百钱买百鸡 ** 枚举方法即为一种归纳的思想**，将问题的所有可能答案一一列举，然后根据条件判断此答案是否合适。 枚举类型题：百钱买百鸡 我国古代数学家张丘建在《算经》中出了一道“百钱买百鸡”的问题， 5文钱可以买一只公鸡，3文钱可以买一只母鸡，1文钱可以买3只雏鸡。 现在用100文钱买100只鸡那么各有公鸡，母鸡，雏鸡多少只？请编写程序实现 题型解析 设一公鸡数量为gj，母鸡数量为mj，小鸡数量为xj， 以单个类型最大范围做数量限制，可列出3组for循环语句， 以此循环出所有
图解、手撕十大排序算法[思路清晰版]
智者之家
08-02 2050
package rank; import java.util.ArrayList; import java.util.Collections; public class CehRank { //１.冒泡排序<时间复杂度Ｏ(n*n),空间复杂读Ｏ(n),稳定排序> public static void maopao(int[] data) { int len = data...
【数据结构】手撕八大排序算法
最新发布
2401_84181145的博客
04-27 795
answer：左边做key，右边先走，可以保证相遇位置比key要小此时有两种情况：1.相遇，left是停着(一定>=key)，right向后走，相遇的位置是left的位置2.相遇，right是停着（一定
面试高频手撕算法 - 背包问题1
xaiobit_hl的博客
10-05 1199
面试高频手撕算法 - 01背包
数据结构与算法之手撕排序算法
希望自己从编程小白变成大佬
04-12 644
为什么要学习排序算法？根据统计，早起大型机CPU资源的四分之一都花在了数据排序上面。排序算法作为最基础的算法，各种操作系统、编程语言都提供了内置的实现。既然排序实现随处可见，我们为什么还要自己动手实现呢？虽然经典算法要动手写写加深印象的道理都懂，但直到最近才发现，每种排序算法里都“暗藏玄机”。排序算法看似简单，其实不同的算法中蕴涵着经典的算法策略。通过熟练掌握排序算法，就可以掌握基本的算法设计思想，包括暴力枚举法、时间空间置换、子问题的分治以及随机化。
前端知识点2——手撕算法
m0_49997078的博客
05-07 832
一、排序 1、冒泡排序 2、快速排序 快速排序,说白了就是给基准数据找其正确索引位置的过程
Python手撕算法Recursion
12-25
Python手撕算法Recursion
Python手撕算法RadixSort
12-25
Python手撕算法RadixSort
Python手撕算法QuickSort
12-25
Python手撕算法QuickSort
Python手撕算法Queue
12-25
Python手撕算法Queue
Python手撕算法mysingleton
12-25
Python手撕算法mysingleton
如何备战面试中的手撕算法
我的博客
04-24 5849
最近，很多同学在微信私聊时提到：“面试中的手撕算法好难啊，网上面经中的算法题基本都不会写，更别提在面试时面对面的十几分钟写出实现代码了…这块到底要怎么准备啊”。 细问下去发现又到一年的春招和实习招聘季节了。距离秋招也就五个月了，五个月的时间看似很长，但等待你们的事情也很多：五个月中你得看厚厚一堆的书籍，并且大部分是得看两到三遍，还有各类框架、源码、数据库、并发、设计模式、操作系统、linux、项目...
面试手撕题 总结
qq_44213041的博客
08-30 259
面试手撕算法题
大厂技术面试中的手撕代码应该如何准备？
weixin_48157259的博客
10-07 3766
不管是秋招还是社招，互联网大厂的技术面试中的手撕代码这一部分总是绕不过去的一关。不只是后端开发和算法岗，现在就连前端、运维、测试、数据等岗位也要考手撕代码了。
手撕算法_adaboost
weixin_44414593的博客
07-24 743
adaboost是典型的boosting算法。 核心思想 boosting算法的核心思想是：上一个模型对单个样本预测的结果越差，下个模型越重视这个样本（增大该样本的权重，加大模型预测错的成本）。提升树就是每个模型都是决策树，提升树种效果比较好的是GBDT和XGBOOST，入门是adaboost。 训练过程（分类） adaboost模型的训练过程可以简单的分为这几步： 1.更新样本权重。 2.训练模型。 3.计算误差。 4.计算该模型的投票权重。back to step1 SAMME算法具体说明： 1.初始化
（手撕）基本算法
weixin_30532837的博客
04-26 256
目录 一、快速排序 1、数组实现 2、链表实现 二、归并排序 1、数组实现 2、链表实现 三、、堆排序 1、大根堆（用来升序）数组存储 2、小根堆（用来降序）数组存储 ...
【初阶数据结构与算法】——手撕八大经典排序算法
m0_70980326的博客
01-30 2962
常见排序算法详解及分析，带你手撕希尔、堆排、快排、归并等经典排序算法
手撕排序算法和个人理解
IRON__MAN__的博客
10-22 614
排序作为最入门的算法，说简单也简单，但是初学者不好想象。下面就做一介绍。 针对于排序算法，我主要关注的点是： 1.代码实现（参杂一些个人的理解） 2.时间，空间复杂度（概念就不介绍了） 3.稳定性 ps：稳定的排序，可以通过代码变成不稳定，不稳定的排序无法变成稳定。界定稳定有一个比较好的办法就是判断有没有跳跃式交换，如果有那么就是不稳定的。如果没有就是稳定的。（这是一个小点，后面会有介绍） 1.直接插入排序 思想：接牌思想，第一个数据默认有序，从第二个数据开始遍历。每次把插入的值放入到tmp中，从它的前一
C和Python手撕机器学习算法1
08-03
在本文中，我们将会手撕机器学习算法1中的C和Python代码。首先，我们需要读取一个csv文件中的数据，然后进行K折交叉验证。接着，我们将使用一些特定的数据集进行测试，这些数据集的数值分别为555.2、121.4和2.1。 ...

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值