软件工程经济学第二章作业
第六题
某软件企业获得10万元的贷款,偿还期为5年,年利率为10%。就下述4种还贷方式,分别计算5年还款总额和还贷额的现值。
1️⃣ 每年末还2万元本金及所欠利息;
金额均以万元为单位,银行利率 i n = 10 % i_n=10\% in=10%
| 年数n | 年初所欠金额 S n − 1 S_{n-1} Sn−1 | 年利息额 I n = S n − 1 i n I_n=S_{n-1}i_n In=Sn−1in | 年终所欠金额 S n = S n − 1 + I n S_n=S_{n-1}+I_n Sn=Sn−1+In | 偿还本金 U n U_n Un | 年终付款总额 V n = U n + I n V_n=U_n+I_n Vn=Un+In |
|---|---|---|---|---|---|
| 1 | 10 | 1 | 11 | 2 | 3 |
| 2 | 8 | 0.8 | 8.8 | 2 | 2.8 |
| 3 | 6 | 0.6 | 6.6 | 2 | 2.6 |
| 4 | 4 | 0.4 | 4.4 | 2 | 2.4 |
| 5 | 2 | 0.2 | 2.2 | 2 | 2.2 |
| ∑ \sum ∑ | 3 | 10 | 13 |
5年还款总额为13万元
还贷额的现值为:
3
(
1
+
10
%
)
+
2.8
(
1
+
10
%
)
2
+
2.6
(
1
+
10
%
)
3
+
2.4
(
1
+
10
%
)
4
+
2.2
(
1
+
10
%
)
5
≈
10
万元
\frac{3}{(1+10\%)}+\frac{2.8}{(1+10\%)^2}+\frac{2.6}{(1+10\%)^3}+\frac{2.4}{(1+10\%)^4}+\frac{2.2}{(1+10\%)^5}\approx 10万元
(1+10%)3+(1+10%)22.8+(1+10%)32.6+(1+10%)42.4+(1+10%)52.2≈10万元
2️⃣ 每年末只还所欠利息,本金在第5年末一次还清;
金额均以万元为单位,银行利率 i n = 10 % i_n=10\% in=10%
| 年数n | 年初所欠金额 S n − 1 S_{n-1} Sn−1 | 年利息额 I n = S n − 1 i n I_n=S_{n-1}i_n In=Sn−1in | 年终所欠金额 S n = S n − 1 + I n S_n=S_{n-1}+I_n Sn=Sn−1+In | 偿还本金 U n U_n Un | 年终付款总额 V n = U n + I n V_n=U_n+I_n Vn=Un+In |
|---|---|---|---|---|---|
| 1 | 10 | 1 | 11 | 0 | 1 |
| 2 | 10 | 1 | 11 | 0 | 1 |
| 3 | 10 | 1 | 11 | 0 | 1 |
| 4 | 10 | 1 | 11 | 0 | 1 |
| 5 | 10 | 1 | 11 | 10 | 11 |
| ∑ \sum ∑ | 5 | 10 | 15 |
5年还款总额为15万元
还贷额的现值为:
1
(
1
+
10
%
)
+
1
(
1
+
10
%
)
2
+
1
(
1
+
10
%
)
3
+
1
(
1
+
10
%
)
4
+
11
(
1
+
10
%
)
5
≈
10
万元
\frac{1}{(1+10\%)}+\frac{1}{(1+10\%)^2}+\frac{1}{(1+10\%)^3}+\frac{1}{(1+10\%)^4}+\frac{11}{(1+10\%)^5}\approx 10万元
(1+10%)1+(1+10%)21+(1+10%)31+(1+10%)41+(1+10%)511≈10万元
3️⃣ 每年末等额偿还本金和利息;
金额均以万元为单位,银行利率 i n = 10 % i_n=10\% in=10%
| 年数n | 年初所欠金额 S n − 1 S_{n-1} Sn−1 | 年利息额 I n = S n − 1 i n I_n=S_{n-1}i_n In=Sn−1in | 年终所欠金额 S n = S n − 1 + I n S_n=S_{n-1}+I_n Sn=Sn−1+In | 偿还本金 U n U_n Un | 年终付款总额 V n = U n + I n V_n=U_n+I_n Vn=Un+In |
|---|---|---|---|---|---|
| 1 | 10 | 1 | 11 | 1.64 | 2.64 |
| 2 | 8.36 | 0.84 | 9.20 | 1.80 | 2.64 |
| 3 | 6.56 | 0.66 | 7.22 | 1.98 | 2.64 |
| 4 | 4.58 | 0.46 | 5.04 | 2.18 | 2.64 |
| 5 | 2.40 | 0.24 | 2.64 | 2.40 | 2.64 |
| ∑ \sum ∑ | 3.2 | 10 | 13.2 |
5年还款总额为13.2万元
还贷额的现值为:
2.64
(
1
+
10
%
)
+
2.64
(
1
+
10
%
)
2
+
2.64
(
1
+
10
%
)
3
+
2.64
(
1
+
10
%
)
4
+
2.64
(
1
+
10
%
)
5
≈
10
万元
\frac{2.64}{(1+10\%)}+\frac{2.64}{(1+10\%)^2}+\frac{2.64}{(1+10\%)^3}+\frac{2.64}{(1+10\%)^4}+\frac{2.64}{(1+10\%)^5}\approx 10万元
(1+10%)2.64+(1+10%)22.64+(1+10%)32.64+(1+10%)42.64+(1+10%)52.64≈10万元
4️⃣ 第五年末一次还清本金和利息。
金额均以万元为单位,银行利率 i n = 10 % i_n=10\% in=10%
| 年数n | 年初所欠金额 S n − 1 S_{n-1} Sn−1 | 年利息额 I n = S n − 1 i n I_n=S_{n-1}i_n In=Sn−1in | 年终所欠金额 S n = S n − 1 + I n S_n=S_{n-1}+I_n Sn=Sn−1+In | 偿还本金 U n U_n Un | 年终付款总额 V n = U n + I n V_n=U_n+I_n Vn=Un+In |
|---|---|---|---|---|---|
| 1 | 10 | 1 | 11 | 0 | 0 |
| 2 | 11 | 1.1 | 12.1 | 0 | 0 |
| 3 | 12.1 | 1.2 | 13.3 | 0 | 0 |
| 4 | 13.3 | 1.3 | 14.6 | 0 | 0 |
| 5 | 14.6 | 1.5 | 16.1 | 1000 | 16.1 |
| ∑ \sum ∑ | 6.1 | 16.1 |
5年还款总额为16.1万元
还贷额的现值为:
16.1
(
1
+
10
%
)
5
≈
10
万元
\frac{16.1}{(1+10\%)^5}\approx 10万元
(1+10%)516.1≈10万元
第九题
某公司计划7年后购进一台设备,约需投资6万元。为此,该公司决定从今年起每年从税后利润中提取等额年金,以作为专用基金存入行。设银行存款年利率为 5.5%,问该公司应提取多少年金。画出相应的现金流量图。
答:
由题目可知
n
=
7
,
S
7
=
6
,
i
=
0.055
n=7,S_7=6,i=0.055
n=7,S7=6,i=0.055,则有
A
=
S
n
⋅
S
F
F
=
S
7
i
(
1
+
i
)
7
−
1
=
6
0.055
(
1
+
0.055
)
7
−
1
=
0.726
万元
A=S_n\cdot SFF=S_7\frac{i}{(1+i)^7-1}=6\frac{0.055}{(1+0.055)^7-1}=0.726万元
A=Sn⋅SFF=S7(1+i)7−1i=6(1+0.055)7−10.055=0.726万元
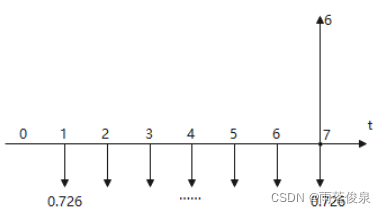
所以该公司应该提取0.726万元,现金流量图如下:
第十三题
某软件企业一年前买了 1 万张面额为 100 元、年利率为 10%(单利)、3 年后到期一次性还本付息国库券。现在有一机会可以购买年利率为 12%、二年期、到期还本付息的无风险企业债券,该企业拟卖掉国库券以购买企业债券,试问该企业可接受的国库券最低出售价格是多少。
答:
(企业债券按照复利)
设该企业可接受的国库券最低出售价格是
p
m
i
n
p_{min}
pmin元/张,则有
10000
×
100
×
(
1
+
3
×
10
%
)
=
10000
×
p
m
i
n
×
(
1
+
12
%
)
2
解得
p
m
i
n
=
103.64
10000\times 100\times(1+3\times 10\%)=10000\times p_{min}\times(1+ 12\%)^2\\ 解得p_{min}=103.64
10000×100×(1+3×10%)=10000×pmin×(1+12%)2解得pmin=103.64
该企业可接受的国库券最低出售价格是103.64元/张
第十四题
某软件项目现有两个设计方案 A 和 A2,为比较这两个设计方案的优劣,该项目主管确定了五个指标 X1、X2、X3、X4、X5,对这五个指标的相对重要性作了两两比较,如表 2.19所示。此外,还确定了每个指标划分为四个等级:U1、U2、U3、U4,各等级的等级分别为5、4、3、1;并对 A1、A2方案的各指标所属等级作了判断,如表 2.20 所示。根据表2.19 和表 2.20 的有关信息,运用基于线性加权和法的关联矩阵法,对这两个软件设计方案的优劣做方案排序。

答:
由题目可得到权重系数求解表如下:
| E i j E_{ij} Eij | X 1 X_1 X1 | X 2 X_2 X2 | X 3 X_3 X3 | X 4 X_4 X4 | X 5 X_5 X5 | F i F_i Fi | W i W_i Wi |
|---|---|---|---|---|---|---|---|
| X 1 X_1 X1 | 1 | 0 | 0 | 1 | 0 | 2 | 2/15 |
| X 2 X_2 X2 | 1 | 1 | 0 | 1 | 0 | 3 | 3/15 |
| X 3 X_3 X3 | 1 | 1 | 1 | 1 | 0 | 4 | 4/15 |
| X 4 X_4 X4 | 0 | 0 | 0 | 1 | 0 | 1 | 1/15 |
| X 5 X_5 X5 | 1 | 1 | 1 | 1 | 1 | 5 | 5/15 |
可以得到价值矩阵表如下:

于是有 V 2 > V 1 V_2>V_1 V2>V1,所以这两个软件设计方案的优劣排序为 A 2 > A 1 A_2>A_1 A2>A1
第十六题
为对计算软件作综合评估,软件协会建立了如表 2.21 所示的指标体系与对应权重,并组织了一个九人专家评审委员会,该委员会对某软件 A 各质量指标(Cj)的所属等级频数分布如表 2.21 所示。试用模糊综合评判法根据表 2.21 的专家评定个人信息对软件 A所属质量做出判断。

答:
由以上等级频数表可以得到A的综合评价表

可以得到A关于四个等级的综合隶属度如下:
V
1
=
0.32
V
2
=
0.36
V
3
=
0.27
V
4
=
0.05
V_1=0.32\\ V_2=0.36\\ V_3=0.27\\ V_4=0.05
V1=0.32V2=0.36V3=0.27V4=0.05
可以得到A的综合价值量为
V
=
∑
j
=
1
4
F
j
⋅
V
j
=
0.32
×
100
+
0.36
×
85
+
0.27
×
70
+
0.05
×
55
=
84.25
V=\sum_{j=1}^4F_j\cdot V_j=0.32\times 100+0.36\times 85+0.27\times 70+0.05\times 55=84.25
V=j=1∑4Fj⋅Vj=0.32×100+0.36×85+0.27×70+0.05×55=84.25
1️⃣ 由最大隶属度规则
max
1
≤
p
≤
4
V
p
=
max
{
0.32
,
0.36
,
0.27
,
0.05
}
=
V
2
\underset{1\le p\le 4}{\text{max}}V_p=\text{max}\{0.32,0.36,0.27,0.05\}=V_2
1≤p≤4maxVp=max{0.32,0.36,0.27,0.05}=V2
由此可知,待评对象A综合评价结果属等级
U
2
U_2
U2
2️⃣ 由最邻近规则
min
1
≤
p
≤
4
∣
V
−
V
p
∣
=
min
{
∣
84.85
−
100
∣
,
∣
84.85
−
85
∣
,
∣
84.85
−
70
∣
,
∣
84.85
−
55
∣
,
}
=
∣
84.85
−
85
∣
=
∣
V
−
F
2
∣
\underset{1\le p\le 4}{\text{min}}|V-V_p|=\text{min}\{|84.85-100|,|84.85-85|,|84.85-70|,|84.85-55|,\}=|84.85-85|=|V-F_2|
1≤p≤4min∣V−Vp∣=min{∣84.85−100∣,∣84.85−85∣,∣84.85−70∣,∣84.85−55∣,}=∣84.85−85∣=∣V−F2∣
由此可知,待评对象A综合评价结果属等级
U
2
U_2
U2








 本文探讨了软件企业四种不同的贷款偿还策略,包括每年末偿还本金和利息、仅还利息、等额偿还和一次性偿还,分析了不同策略的5年还款总额及其现值。此外,还涉及了软件项目设计方案的评估方法,以及基于模糊综合评判法对软件质量的评判过程。
本文探讨了软件企业四种不同的贷款偿还策略,包括每年末偿还本金和利息、仅还利息、等额偿还和一次性偿还,分析了不同策略的5年还款总额及其现值。此外,还涉及了软件项目设计方案的评估方法,以及基于模糊综合评判法对软件质量的评判过程。

















 1015
1015

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










