[XJTUSE编译原理]第四章 语法分析——自上而下分析

第四章 语法分析——自上而下分析

语法分析的前提

对语言的语法结构进行描述

采用正规式和有限自动机描述和识别语言的单词符号

用上下文无关文法来描述语法规则

语法分析的任务:分析一个文法的句子的结构

语法分析器的功能:按照文法的产生式(语言的语法规则)，识别输入符号串是否为一个句子(合式程序)

语法分析的方法

1️⃣ 自上而下Top-down

从文法的开始符号出发,反复使用各种产生式，寻找"匹配"的推导

推导：根据文法的产生式规则,把串中出现的产生式的左部符号替换成右部

从树的根开始，构造语法

递归下降分析法、预测分析程序

2️⃣ 自下而上Bottom-up

从输入串开始， 逐步进行归约,直到文法的开始符

归约：根据文法的产生式规则,把串中出现的产生式的右部替换成左部符号

从树叶节点开始,构造语法树

算符优先分析法、LR分析法

语法分析的任务与分类

语法分析的任务：$对任一给定w\in V_T^{\ast },判断w\in L(G)$

w表示终结符串

句子的全体是一个语言，记作L(G)

语法分析器是一个程序，它按照P，做识别w的工作

自上而下分析面临的问题

主旨：从文法开始符号出发，自上而下地为输入串建立一棵语法树。

举例：文法G1: S -> cAd A -> ab|a，输入串：w=cad，为它建立语法树

上述分析方法的实现：

1️⃣ 每一非终结符对应一个递归子程序，在只生成两个串的文法中过程无须递归;但是，对于生成无数个串的文法而言，递归不可避免。

2️⃣ 递归子程序是一个布尔过程，一旦它发现自己的某个候选式与输入串匹配，它就按此式扩充语法树，返回true,指针移过已匹配子串;否则，返回false,保持原来的语法树和指针不变。

程序实现

使用两个过程: S()和A()， 它们送回true or false,决定于它们是否在输入串中找到相应的终结符所构成的串。

使用记号

input_ symbol:当前符号内容
input_ pointer: 输入字符指针

使用过程

ADVANCE():把input_ pointer移 到下一输入符号位置，置input_symbol是当前符号内容。

procedure S();
begin 
	if input_symbol = 'c' then
	begin
		ADVANCE();
		if A() then//A扩展
			if input_symbol = 'd'
			then 
				begin
					ADVANCE();//指针后移
					return true;
				end;
	end;
	return false;
end;

procedure A();
begin
	isave := input_pointer;//记录输入指针，防止回滚
	if input_symbol = 'a' then
	begin
		ADVANCE();
		if input_symbol = 'b' then
			begin
				ADVANCE();
				return true;
			end;
	end;
/* 匹配ab失败，则匹配a*/
	input_pointer := isave//将之前记录的输入指针赋值给输入指针
	if input_symbol = 'a' then
		begin
			ADVANCE();
			return true;
		end;
	else
		return false;
end;

困难和问题

• 文法的左递归
• 回溯
• 使用候选式的顺序会影响所接受的语言: 如: A -> ab|a改为A->a|ab
• 难以报告出错的确切位置
• 穷举试探法一 低效的分析方法

自上而下分析的问题如何解决

消除文法左递归以及回溯问题

区分三种类型的左递归

1️⃣ 直接左递归

形如：N->Nα

2️⃣ 间接左递归

形如：N->Aα A->Bβ B->Nγ

3️⃣ 潜在左递归

形如：N->α N β，而$\alpha \stackrel{+}{\Rightarrow }\epsilon$

直接左递归的消除

候选式：A->Aα|β，可以得到文法符号串：βα、βαα、βααα……

​ A->βA’ A’->α A’|ε，也可以得到文法符号串：βα、βαα、βααα……

一般化可以得到直接左递归的消除方法

若：A->Aα|β，其中β不以A开头，则修改规则为A->βA’ A’->α A’|ε

可以进行推广：假定P的全部产生式为
$$P\to P{\alpha }_1|P{\alpha }_2|...|P{\alpha }_m|{\beta }_1|{\beta }_2|...|{\beta }_n$$
每个α都不等于ε，每个β都不以P开头

则将左递归变为右递归如下
$$\begin{gathered} P\to {\beta }_1{P}^{\prime }|{\beta }_2{P}^{\prime }|...|{\beta }_n{P}^{\prime } \\ {P}^{\prime }\to {\alpha }_1{P}^{\prime }|{\alpha }_2{P}^{\prime }|...|{\alpha }_m{P}^{\prime }|\epsilon \end{gathered}$$

举例：文法：E->E+T|T T->T*F|F F->(E)|i

消除直接左递归后

E->TE’

E’->+TE’|ε

T->FT’

T’->*FT’|ε

F->(E)|i

间接和潜在左递归的消除

一个文法消除左递归的条件：不含以ε为右部的产生式；不含回路$P\stackrel{+}{\Rightarrow }P$

代入法

将一个产生式规则右部的a中的非终结符N替换为“N的候选式”。如果N有n个候选式，则右边的a重复n次，而且每一次重复都用N的不同候选式来代替N。

举例：（改写之后的）N->a|Bc|ε在S->pNq中的代入结果：S->paq|pBcq|pq

消除一个文法一切左递归的算法

1️⃣ 对文法G的所有非终结符进行排序；

2️⃣ 按上述顺序对每一个非终结符Pi依次执行：

for(j=1;j< i-1；j++)
	将Pj代入Pi的产生式（若可代入的话);
消除关于Pi的直接左递归;

3️⃣ 化简上述所得文法。

举例

对于文法：S->Qc|c Q->Rb|b R->Sa|a

虽然没有直接左递归，但是S,Q,R都是左递归的，比如有S=>Qc=>Rbc=>Sabc

1️⃣ 将非终结符排序为：R、Q、S

2️⃣ 对于R，不存在直接左递归，将R带入到Q的有关候选后，我们把Q的规则变为Q->Sab|ab|b

现在的Q同样不含有直接左递归，把它带入到S的有关候选后，S变为S->Sabc|abc|bc|c，消除S的直接左递归，可以得到整个文法

S->abcS’|bcS’|cS’

S’->abcS’|ε

Q->Sab|ab|b

R->Sa|a

其中Q和R的规则已经多余，化简以后可以得到

S->abcS’|bcS’|cS’

S’->abcS’|ε

由于排序不同，最后得到的文法在形式上可能不一样，但是都是等价的

消除回溯、提左因子

回溯原因

若当前符号 = a，对 A 展开，而 A -> α1|α2|…|αm那么，要知道哪一个αi是获得以a开头的串的唯一替换式。

即：选择哪一个αi，亦即通过查看第一个（当前）符号来发现合适的替换式α。

如何选择αi？

以a为开头的αi

如果有多个αi以a开头，则这是文法的问题

举例

有产生式

语句->if 条件 then 语句 else 语句|while 条件 do 语句|begin 语句表 end

若要寻找一个语句，那么关键字if，while，begin就提示我们哪一个替换式是最右可能成功的替换式

若要求不得回溯，文法G（不含有左递归）的必要条件是什么？

若由${\alpha }_i\stackrel{+}{\Rightarrow }a...$(某个文法符号串经过若干步推导可以得到以a（终结符）开头的串)，选该αi必中，但若${\alpha }_j\stackrel{+}{\Rightarrow }a...$,就会导致无法百发百中。解决办法是对文法本身提出要求:不要出现以上情况”。把上述要求阐明清楚可以采用如下定义的FIRST(α),即α的首符集。由于空串的存在，不能称为首终结符集。

首符集定义FIRST(α)
F I R S T ( α ) = { a ∣ α ⇒ ∗ a … ， a ∈ V T } i f   α ⇒ ∗ ε , d e f i n e   ε ∈ F I R S T ( α ) FIRST(\alpha)=\{a|\alpha\overset{*}{\Rightarrow}a…，a\in V_T\}\\ if\ \alpha\overset{*}{\Rightarrow}ε,define\ ε\in FIRST(\alpha) FIRST(α)={a∣α⇒∗a…，a∈VT​}if α⇒∗ε,define ε∈FIRST(α)

定理

若一个$A\in V_N$有许多$FIRST({\alpha }_i)$。如果A的任何两个候选式${\alpha }_i$和${\alpha }_j$之间均满足
$$FIRST({\alpha }_i)\cap FIRST({\alpha }_j)=\varnothing$$
意味着，A的每一候选式α推导后所得的字符串第一个$V_T$均不同。

于是，对输入符号α,如果α∈FIRST(αi), 则α not∈FIRST(αj), (j≠i)。因此，对A的展开无疑应选候选式αi,否则无法命中。

消除回溯目的

使非终结符A所有候选式的首符集两两不相交

方法：提取公共因子

若：$A->\delta {\beta }_1|\delta {\beta }_2|...|\delta {\beta }_n|{\gamma }_1|{\gamma }_2|...|{\gamma }_m$，其中每个γ不以δ开头

那么可以把这些规则改写成
$$\begin{gathered} A\to \delta A^{\prime }|{\gamma }_1|{\gamma }_2|...|{\gamma }_m \\ {A}^{\prime }\to {\beta }_1|{\beta }_2|...|{\beta }_n \end{gathered}$$

递归下降分析程序构造

在不含左递归和每个非终结符的所有候选式的首符集都两两不相交条件下，构造一个不带回溯的自上而下分析程序,该分析程序由一组递归过程组成，每个过程对应文法的一个非终结符。这样的一个分析程序称为递归下降分析器。

举例

文法G:

E->TE’

E’=>+TE’|ε

T->FT’

T’->*FT’|ε

F->(E)|i

每个非终结符对应的递归子程序如下：

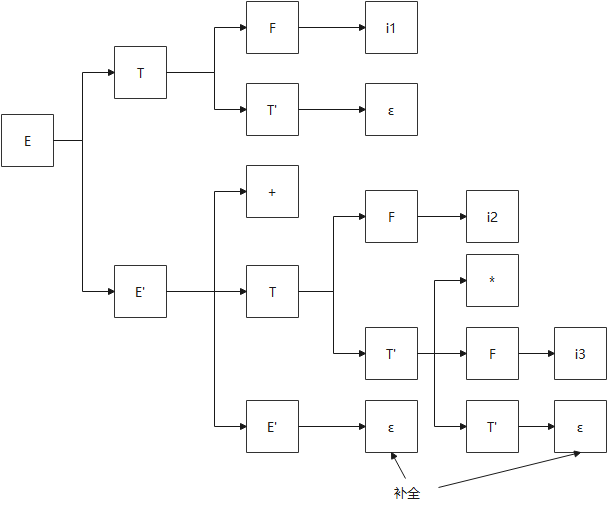
面临输入：i1+i2*i3的分析步骤如下

构造语法树时，注意点

有ε，自动匹配，不会失败

无成功/失败消息返回

出错位置不确切

构造递归下降分析程序时，它由一组递归过程组成。每个递归过程对应文法的一个非终结符。

预测分析程序

❓ 问题：
用递归子程序描写递归下降分析器，要求实现该编译程序的语言（高级或汇编）允许递归。

🚗 改进：
使用一张分析表和一个栈同样可实现递归下降分析。用这种方法实现的语法分析程序叫预测分析程序。

预测分析程序的工作过程

预测分析表事先已经准备好了。

预测分析程序有四部分

1️⃣ 一个输入:含有要分析的终结符串，右端有#。

2️⃣ 一个栈:栈底是#，栈内是一系列文法符号;开始时，#和S先进栈。

3️⃣ 分析表:二维数组M[A, a], 其中$a\in V_T;A\in V_N$，#要占一列，多了一列

4️⃣ 输出:根据分析表内元素做规定的语法分析动作。

分析程序的动作

程序测定栈顶符号X和当前输入符号a,由(X, a)决定程序动作，三种可能:

1️⃣ 若X=a=#，分析停止，宣告成功地完成分析;

2️⃣ 若X=a≠#,则X弹出栈，前移输入指针;

3️⃣ 若$X\in V_N$,则去查分析表M的元素M[X,a],该元素或为X的产生式，或为一个出错元素。

对第3)条，$X\in V_N$，查分析表M的元素M[X, a]后

如:M[X,a]={X->UVV},就用WVU(U在顶)替换栈顶的X;

如: M[X, a]=error,则调用error程序。

分析表格式

文法G:

E->TE’

E’=>+TE’|ε

T->FT’

T’->*FT’|ε

F->(E)|i

	id	+	*	(	)	#
E	E->TE’			E->TE’
E’		E’->TE’			E’->ε	E’->ε
T	T->FT’			T->FT’
T’		T’->ε	T’->*FT’		T’->ε	T’->ε
F	F->id			F->(E)

#（界符）视为特殊的终结符

所有的行跟非终结符对应，所有的列跟终结符对应

隐去了出错处理

举例说明

按照预测分析程序，对于输入id+id*id所作

结论

①输出的产生式就是最左推导的产生式。栈中放右部，等待与α匹配；

②分析表中出现（栈顶，a）时，指出如何扩充树，并且能马上发现错误。

实质

栈：残缺规范句型

表：指出$V_N$按哪一条扩充，依赖于$V_T$

分析表的构造[考点]

按照$\alpha \stackrel{\ast }{\Rightarrow }？$将产生式分成两种

$\alpha \stackrel{\ast }{\Rightarrow }a\dots \dots$

$\alpha \stackrel{\ast }{\Rightarrow }\epsilon$

先要构造两个与G有关的集合：FIRST(α)首符集和FOLLOW(A)后继符集(跟在非终结符A后面的终结符)

1️⃣ 定义：对于文法G，$\alpha \in V\ast$，S、A$\in V_N$
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ &\text{FIRST}(…

2️⃣ 构造FIRST(α)

🍎 对于单符号：先构造$FIRST(X),X\in V_T\cup V_N$

连续应用以下规则，直到再无终结符或ε加入任一FIRST集为止

① 若$X\in V_T$，则FIRST(X)={X}

② 若$X\in V_N,且X\to a\alpha$，则{a}∪FIRST(X)；若$X\in V_N,且X\to \epsilon$，则{ε}∪FIRST(X)

③ 若$X\in V_N,且X\to Y\dots ，Y\in V_N$，则FIRST(Y)\{ε}∪FIRST(X)；若$X\to Y_1{Y}_2\dots Y_k，Y_1,...,Y_{i-1}\in V_N$是一个产生式，而且对于任何j，$1\le j\le i-1$，$FIRST(Y_j)$中都含有ε，即$Y_1...Y_{i-1}\stackrel{\ast }{\Rightarrow }\epsilon$,则把$FIRST(Y_i)$中的所有非ε元素加入到FIRST(X)中；如果所有的$FIRST(Y_j)，j=1,2,...,k$都有ε，则把ε也加入FIRST(X)

所有的非终结符最后都会变成终结符串

🍎 对于符号串：再进而构造$FIRST(X_1{X}_2...X_n)即FIRST(\alpha )$

① $FIRST(X_1)$的非ε终结符加入$FIRST(\alpha )$

② 若$$\epsilon \in FIRST(X_1)$$,则$FIRST(X_2)$的所有非ε终结符加入$FIRST(\alpha )$

③ 若$$\epsilon \in FIRST(X_1)，\epsilon \in FIRST(X_2)$$,则$FIRST(X_3)$的所有非ε终结符加入$FIRST(\alpha )$

最后，若$\epsilon \in FIRST(X_i),i=1,...,n$，则{ε}加入$FIRST(\alpha )$

终结符、非终结符、文法符号串、候选式都可以构造首符集；后继符集只能用终结符定义！

3️⃣ 构造FOLLOW(A)

对于文法G的每个非终结符A构造FOLLOW(A)的办法是，连续使用下面的规则，直到每个FOLLOW不再增大为止

① 对于文法的开始符号S，置#于FOLLOW(S)中——#不能忽视！

② 若$A\to \alpha B\beta$，则把FIRST(β)\{ε}加入到FOLLOW(B)中

③ 若有$A\to \alpha B$。或者$A\to \alpha B\beta$是一个产生式而$B\Rightarrow \epsilon$(即ε∈FIRST(β))，则把FOLLOW(A)加入到FOLLOW(B)中

✅举例1✅

已知文法G:
E->TE’ T’->*FT’|ε E’->+TE’|ε F->(E)|i T->FT’
求它的FIRST(α)，FOLLOW(A)

1️⃣ 构造首符集

首先看产生式右边，如果第一个符号是终结符，则把其加入非终结符的首符集中，再看一下候选式中有没有ε，有的话也加入首符集中，如由F->(E)|i可知 F I R S T ( F ) = { ( , i } FIRST(F)=\{(,i\} FIRST(F)={(,i}

还有一些推到关系，如T->FT’,E->TE’，则F首符集中非ε的元素也是T中首符集的元素,T首符集中非ε的元素也是E中首符集的元素:FIRST(F)={ ( , i }=FIRST(T)=FIRST(E)

2️⃣ 构造非终后继符集

由法则①：FOLLOW(E)={#}

由法则②

E->TE’，则将 FIRST(E’) \ {ε} 加入 FOLLOW(T)：FOLLOW(T)={+}

T->FT’，则将 FIRST(T’) \ {ε} 加入 FOLLOW(F)：FOLLOW(F)={*}

F->(E)，则将FIRST( ) )加入FOLLOW(E)：FOLLOW(E)={ # , ) }

由FISRT①，FIRST( ) )=）

由法则③

E->TE’，将FOLLOW(E)加入到FOLLOW(E’)中:FOLLOW(E’)={ ) , #}}

E->TE’，且E’->ε，则将FOLLOW(E)加入到FOLLOW(T)中：FOLLOW(T)={ + , ) , #}

T->FT’，将FOLLOW(T)加入到FOLLOW(T’)中：FOLLOW(T’)={ + , ) , #}

T->FT’，且T’->ε，将FOLLOW(T)加入到FOLLOW(F)中：FOLLOW(F)={*, + , ) , #}

首符集	后继符集
FIRST(E)={ ( , i }	FOLLOW(E)={ ) , #}
FIRST(E’)={+ , ε}	FOLLOW(E’)={ ) , #}}
FIRST(T)={ ( , i }	FOLLOW(T)={ + , ) , #}
FIRST(T’)={* , ε}	FOLLOW(T’)={ + , ) , #}
FIRST(F)={ ( , i }	FOLLOW(F)={*, + , ) , #}

4️⃣ 分析表的构造

算法：输入：G1文法，输出：分析表M

① 对文法的每一个A->α，做②和③

② 对于任一a∈FIRST(α)，把A->α加入到M[A，a]（可能不止一个）

③ 若ε∈FIRST(α)，则把A->α加入M[A，b]，b∈FOLLOW(A)；若ε∈FIRST(α)，#∈FOLLOW(A)，则把A->α加进M[A,#]

④ 把所有无定义的M[A，a]标上“出错标志”

✅举例2✅

将算法应用于上述文法G：E->TE’ T’->*FT’|ε E’->+TE’|ε F->(E)|i T->FT’

① E->TE’

因为FIRST(TE’)=FIRST(T)={(,i)}，即产生式E->TE’保证了M[E，i]和M[E, (]中持有E->TE’

所以M[E，(]={E->TE’} M[E，id]={E->TE’}

② E’->+TE’

因为FIRST(+TE’)={+}，所以M[E’，+]={E’->+TE’}

③ E’->ε

因为有ε，需要去看产生式的左部非终结符的FOLLOW集中有哪些终结符

FOLLOW(E’)={),#}，所以M[E’,)]={E’->ε}，M[E’，#]={E’->ε}

最终可以得到如下分析表

	id	+	*	(	)	#
E	E->TE’			E->TE’
E’		E’->TE’			E’->ε	E’->ε
T	T->FT’			T->FT’
T’		T’->ε	T’->*FT’		T’->ε	T’->ε
F	F->id			F->(E)

上述算法可应用于任何文法G以构造它的分析表M。但对于某些文法，有些M[A,a]可能持有若干个产生式，或者说有些M[A,a]可能是多重定义的。如果G是左递归或二义的，那么，M至少含有一个多重定义人口。因此，消除左递归和提取左因子将有助于获得无多重定义的分析表M。

可以证明，一个文法G的预测分析表M不含多重定义入口，当且仅当该文法为LL(1)的。

LL(1)文法

LL：第一个L表示从左到右扫描输入串；第二个L表示最左推导

(1)：表示分析时每一步只需要向前查看一个符号

LL(1)文法

一个文法G，若它的分析表M不含多重定义入口(同一个格子里面有两个产生式)，则称它为一个LL(1)文法

LL(1)文法的条件

文法G式LL(1)的，则对于G的每一个非终结符A的任何两个不同产生式A->α|β，有：

1️⃣ FIRST(α)∩FIRST(β)=Φ

2️⃣ 若某一个候选式$\beta \stackrel{\ast }{\Rightarrow }\epsilon$，则FIRST(α)∩FOLLOW(A)=Φ

🍌 说明

使用LL(1)文法，一定可以实现不带回溯的自上而下分析

若某文法G为LL（1)文法，则下列那些描述正确？

✅该文法的预测分析表必无多重入口。

✅所有非终结符各候选式的首符集两两之间交集必为空。

✅非终结符的某个候选式的首符集中有空串时，该非终结符的后继符集与其余各个候选式首符集交集必为空。

但是，条件语句文法不能改造成LL(1)文法

语句->if 条件 then 语句 else 语句|if 条件 then 语句

例如：S->iCtS|iCtSeS|a C->b

提公因子以后，文法变为S->iCtSS’|a S’->eS|ε C->b

计算该文法的FIRST集和FOLLOW集如下：

FIRST(S)={i，a} FIRST(S’)={e，ε} FIRST©={b}

FOLLOW(S)={#，e} FOLLOW(S’)={#，e} FOLLOW©={t}

分析表如下：

	a	b	e	i	t	#
S	S->a			S->iCtSS’
S’			S’->eS
C		C->b

上表未填满

对于候选式S’->ε，因为ε∈FIRST(S’)={e，ε}，而FOLLOW(S’)={#，e}，所以S’->ε填入M[S’,#]和M[S’，e]，有多重入口，不是LL(1)文法

解决：强制令M[S’，e]={S’->eS}，即坚持将e与最近的t相结合，从程序语言来看，相当于规定ELSE坚持与最近的THEN相结合

参考资料

[1] 西安交通大学软件工程专业编译原理 吴晓军 2022春

[2] 陈火旺，刘春林，谭庆平，赵克佳，刘越. 程序设计语言编译原理（第3版）. 北京：国防工业出版社，2010